SSIM introducerades först i 2004 IEEE-papper, Bildkvalitetsbedömning: från Felsynlighet till strukturell likhet. Abstraktet ger en bra intuition i tanken bakom det föreslagna systemet,
objektiva metoder för att bedöma perceptuell bildkvalitet försökte traditionellt kvantifiera synligheten för fel (skillnader) mellan en förvrängd bild och en referensbild med hjälp av en mängd kända egenskaper hos det mänskliga visuella systemet. Under antagandet att mänsklig visuell uppfattning är mycket anpassad för att extrahera strukturell information från en scen, introducerar vi ett alternativt kompletterande ramverk för kvalitetsbedömning baserad på nedbrytning av strukturell information.
sammanfattning: författarna gör 2 viktiga punkter,
- de flesta bildkvalitetsbedömningstekniker är beroende av att kvantifiera fel mellan en referens och en exempelbild. Ett vanligt mått är att kvantifiera skillnaden i värdena för var och en av motsvarande pixlar mellan provet och referensbilderna (genom att till exempel använda Medelkvadratfel).
- det mänskliga visuella uppfattningssystemet är mycket kapabelt att identifiera strukturell information från en scen och därmed identifiera skillnaderna mellan informationen extraherad från en referens och en provplats. Därför kommer ett mått som replikerar detta beteende att fungera bättre på uppgifter som innebär att man skiljer mellan ett prov och en referensbild.
metriska Strukturlikhetsindex (ssim) extraherar 3 Viktiga funktioner från en bild:
- luminans
- kontrast
- struktur
jämförelsen mellan de två bilderna utförs på grundval av dessa 3 funktioner.
Fig 1 nedan visar arrangemanget och flödet av det strukturella Likhetsmätningssystemet. Signal X och Signal Y hänvisar till referens-och Exempelbilderna.

men vad beräknar denna metriska?
detta system beräknar det strukturella Likhetsindexet mellan 2 givna bilder som är ett värde mellan -1 och + 1. Ett värde på +1 indikerar att de 2 givna bilderna är mycket lika eller samma medan ett värde på -1 indikerar att de 2 givna bilderna är mycket olika. Ofta justeras dessa värden för att ligga i intervallet , där ytterligheterna har samma betydelse.
låt oss nu kort undersöka hur dessa funktioner representeras matematiskt och hur de bidrar till den slutliga SSIM-poängen.
- luminans: luminans mäts genom medelvärde över alla pixelvärden. Dess betecknade med Pov (Mu) och formeln ges nedan,
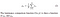
- Kontrast: Det mäts genom att ta standardavvikelsen (kvadratroten av varians) för alla pixelvärden. Den betecknas med Pov (Sigma) och representeras av formeln nedan,
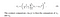
- Struktur: Den strukturella jämförelsen görs med hjälp av en konsoliderad formel (mer om det senare) men i huvudsak delar vi insignalen med dess standardavvikelse så att resultatet har enhetsstandardavvikelse vilket möjliggör en mer robust jämförelse.
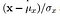
så nu har vi etablerat den matematiska intuitionen bakom de tre parametrarna. Men vänta! Vi är ännu inte färdiga med matematiken, lite mer. Vad vi saknar nu är jämförelsefunktioner som kan jämföra de två givna bilderna på dessa parametrar, och slutligen en kombinationsfunktion som kombinerar dem alla. Här definierar vi jämförelsefunktionerna och slutligen kombinationsfunktionen som ger likhetsindexvärdet
- Luminansjämförelsefunktion: den definieras av en funktion, l(x, y) som visas nedan. Mu (Mu) representerar medelvärdet av en given bild. x och y är de två bilderna som jämförs.
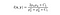
där C1 är en konstant för att säkerställa stabilitet när nämnaren blir 0. C1 ges av,
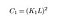
Uppdatering: under hela artikeln hade vi inte undersökt vad K-och L-konstanterna i denna ekvation är. Tack och lov en läsare påpekade att i kommentarerna, och så för att göra den här artikeln lite mer användbar, jag ska bara definiera dem här.
L är det dynamiska området för pixelvärden (vi ställer in det som 255 eftersom vi har att göra med standard 8-bitars bilder). Du kan läsa mer om vad som är de olika bildtyperna och vad de betyder här.
K1, K2 är bara normala konstanter, inget mycket där!
- kontrastjämförelsefunktion: den definieras av en funktion c(x, y) som visas nedan. i den här artikeln anges standardavvikelsen för en given bild. x och y är de två bilderna som jämförs.
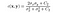
där C2 ges av,
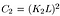
- struktur jämförelse funktion: den definieras av funktionen s(x, y) som visas nedan. i den här artikeln anges standardavvikelsen för en given bild. x och y är de två bilderna som jämförs.
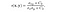
där XY (XY) definieras som,
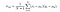
och slutligen ges ssim-poängen av,

där > 0, > 0, > 0 anger den relativa betydelsen av var och en av mätvärdena. För att förenkla uttrycket, om vi antar, kan vi få,
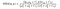
men det finns en plot twist!
medan du skulle kunna implementera SSIM med hjälp av ovanstående formler är chansen att det inte kommer att vara lika bra som de färdiga implementeringarna som finns tillgängliga, eftersom författarna förklarar det,
för bildkvalitetsbedömning är det användbart att tillämpa ssim-indexet lokalt snarare än globalt. För det första är bildstatistiska funktioner vanligtvis mycket rumsligt icke-stationära. För det andra kan bildförvrängningar, som kanske eller inte beror på den lokala bildstatistiken, också vara rymdvariant. För det tredje, vid typiska visningsavstånd, kan endast ett lokalt område i bilden uppfattas med hög upplösning av den mänskliga observatören på en gång (på grund av foveation-funktionen hos HVS , ). Och slutligen kan lokaliserad kvalitetsmätning ge en rumsligt varierande kvalitetskarta över bilden, som ger mer information om kvalitetsnedbrytningen av bilden och kan vara användbar i vissa applikationer.
sammanfattning: Istället för att tillämpa ovanstående mätvärden globalt (dvs. över hela bilden på en gång) är det bättre att tillämpa mätvärdena regionalt (dvs. i små delar av bilden och ta medelvärdet totalt).
denna metod kallas ofta det genomsnittliga strukturella Likhetsindexet.
på grund av denna förändring i tillvägagångssätt förtjänar våra formler också ändringar för att återspegla detsamma (det bör noteras att detta tillvägagångssätt är vanligare och kommer att användas för att förklara koden).
(Obs: Om innehållet nedan verkar lite överväldigande, inga bekymmer! Om du får kontentan av det, sedan gå igenom koden kommer att ge dig en mycket tydligare uppfattning.)
författarna använder en 11×11 cirkulär-symmetrisk Gaussisk Vägningsfunktion (i grunden en 11×11-matris vars värden härrör från en gaussisk fördelning) som flyttar pixel-för-pixel över hela bilden. Vid varje steg beräknas lokal statistik och ssim-index i det lokala fönstret. Eftersom vi nu beräknar mätvärdena lokalt revideras våra formler som,
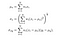
där wi är den gaussiska viktningsfunktionen.
om du hittade det här lite ointuitivt, inga bekymmer! Det räcker att föreställa sig wi som en multiplikationoch som används för att beräkna de önskade värdena med hjälp av några matematiska knep.
när beräkningar utförs över hela bilden tar vi helt enkelt medelvärdet av alla lokala SSIM-värden och kommer fram till det globala SSIM-värdet.
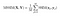
äntligen klar med teorin! Nu till koden!