förenkla FEA modeller: plan Stress och plan stam

Redaktörens anmärkning: Tony Abbey undervisar levande NAFEMS FEA klasser i USA, Europa och Asien. Han undervisar också NAFEMS e-learning klasser globalt. Kontakt .för detaljer.

en tidigare Skrivbordsteknisk artikel (”förenkla Fea-simuleringsmodeller med plan symmetri”) förklarade att även med kraftfulla moderna datorer finns det ofta en motivation att använda förenklingstekniker i strukturell finita elementanalys (FEA). Denna uppföljning beskriver hur två närbesläktade metoder kan användas för att ta 2D-skivor genom en komplex struktur i intressanta regioner. De resulterande FEA-modellerna kan ge värdefull inblick i lokala påfrestningar snabbare och effektivare än en full 3D-modell. De kommer inte att berätta hela historien, men är värdefulla verktyg för CAE-ingenjören.

de två FEA-metoderna kallas planspänning och planstam. Båda använder 2D plana element som ser ut som tunna skalelement och är maskade med plan ytgeometri.

Planspänningsanalys

Fig. 1 visar viktiga fakta om planstressanalys. Den strukturella regionen antas ligga i 2D xy-planet, med den tredje strukturella dimensionen relativt liten. I figuren är detta tjockleken i z-riktningen. Spänningar finns i 2D-planet som sigma x, sigma y (direktspänningar) och sigma xy (skjuvspänning I plan). Var och en av dessa spänningar är konstant genom tjockleken som visas i insatsen. Dessutom kan det inte finnas någon stress i z-riktningen. Detta stress-töjningsmaterialförhållande definieras i 2D-planspänningselement som används i denna typ av analys.

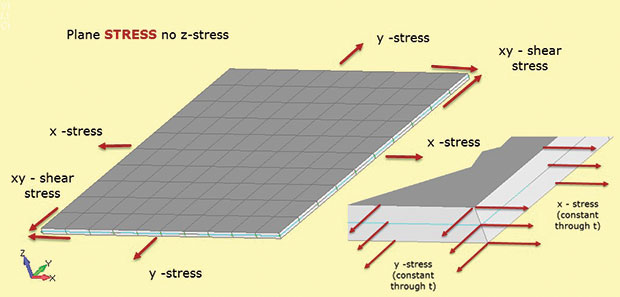Fig. 1: Plan stress; spänningstillstånd antaganden.

bristen på z-stress är sättet att komma ihåg elementets typbeteckning planspänning (dvs. endast i planspänningar tillåts). Det finns inte heller några skjuvspänningar genom tjocklek. Vi kunde ladda planspänningsmodellen i Fig. 1 med en bi-axiell belastning och beräkna Sigma x och Sigma y. Det finns ingen Sigma z. vi kan också beräkna motsvarande in-plan stammar e – x och e-y. om vi tillämpar en skjuvbelastning kan vi hitta skjuvspänning sigma xy och skjuvstam e-xy. Intressant kan vi också beräkna genomtjockleksstammen e-z. Detta är inte noll, eftersom modellen är fri att tunna ner i z eftersom den sträcker sig i x och y.Det finns ingen begränsning utanför planet för att förhindra detta. I vissa lösare kan vi återvinna genom tjockleken stam e-z och använda den för att beräkna förändringen i tjocklek. (Om modellen är i bi-axiell kompression blir z-sektionen tjockare). Detta anses vanligtvis vara en sekundär stam och kanske inte är tillgänglig för utmatning—men det är där och kan beräknas manuellt om det behövs.

Fig. 2 visar en aluminium klack komponent. Klacken sticker ut från en sammansatt arkuppläggning som har skikt placerade och bundna över tangarna (eller benen) och underkroppssektionen. Tangarna överför lasten som appliceras på klacken till kompositstrukturen. I praktiken skulle skikten trampas för att möjliggöra en jämn skjuvöverföring genom bindningen till kompositen. Skjuvöverföringen till kompositen simuleras här genom diffusa ytdragkrafter som ”drar” på tangarna. Dessa balanserar den applicerade klackbelastningen.

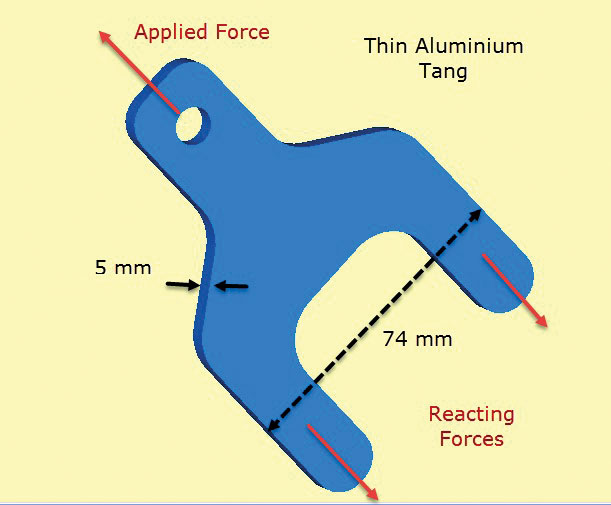Fig. 2: Tunnväggiga aluminium tang överföra lasten till kompositstruktur.

det viktigaste antagandet här är att genom tjockleksspänningar är noll och in-planspänningarna är konstanta genom tjockleken i komponenten. Detta innebär att den lokala detaljerna i skjuvbelastningsöverföringen från komposit till tang är dåligt modellerad. Men fokus för denna analys är att kontrollera dimensionering av klack och tang tvärsnitt klart av kompositen, med användning i planet spänningar.

komponentens tjocklek är liten jämfört med andra dimensioner. Detta värde matas in som den faktiska tjockleken i definitionen av planspänningselement.

Fig. 3 visar FEA-modellen och de beräknade maximala huvudspänningarna. Intresseområdena ligger runt klacken och axelradierna. I den verkliga världen skulle stresstillståndet vid spänningskoncentrationerna vara 3D och genom tjocklek Sigma z-spänningar och skjuvspänningar skulle balansera lokalt. Det är dock mycket rimligt här att anta att spänningen i planet dominerar. Detta är samma antagande implicit i de flesta traditionella spänningskoncentration (Kt) beräkningar som finns i handböcker.

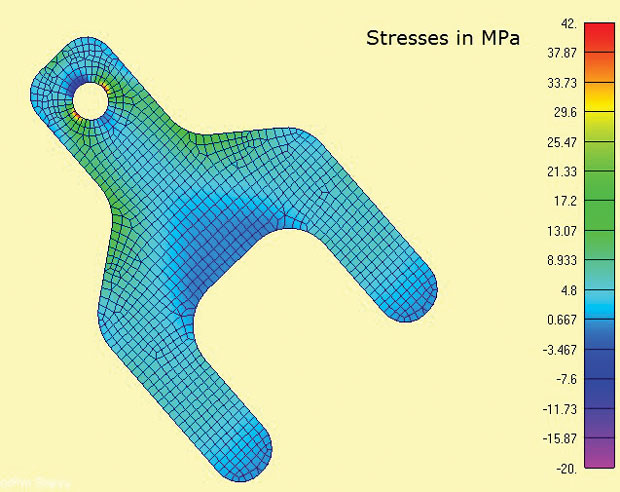Fig 3: 2D-planspänningselement som visar maximala huvudspänningar

en av de praktiska funktionerna i planspänningsanalysen är att det är en strikt 2D-analys, så endast tre frihetsgrader (DOF) måste begränsas (översättningar i plan x, y och rotation om z-axeln). Detta lämpar sig för 3-2-1 minsta begränsningsmetod med balanserad belastning. I ett 2D-fall degenererar detta till en 2-1-metod. En nod har DOF x och y begränsad, en andra lämplig ortogonal nod har DOF x begränsad. Detta gör att reaktionsbelastningen i tangarna kan appliceras direkt som diffusa balanseringsbelastningar. Det skulle vara svårt att simulera detta gränsvillkor via begränsningar till marken.

E-Z-stammen genom tjockleken och därmed gallring av tangarna kunde beräknas som en sekundär effekt.

Planstam Analys

Fig. 4 visar kärnan i planstammetoden. Återigen används 2D plana element, men med subtilt olika antaganden. Planspänningarna x, y och xy utvecklas som tidigare. Men den här gången är det out-of-plane, eller genom tjocklek z stam som är inställd på noll. Så planstamanalys tillåter endast stammar i planet. Detta fungerar bra för att representera tjocka strukturer som visas. Närvaron av detta mycket material tenderar att stabilisera komponenten och förhindra att den spänner i z. Detta innebär också att konstanta genomtjocklek Z-spänningar utvecklas i strukturen. Detta stress-töjningsmaterialförhållande definieras i 2D-planspänningselement som används i denna typ av analys.

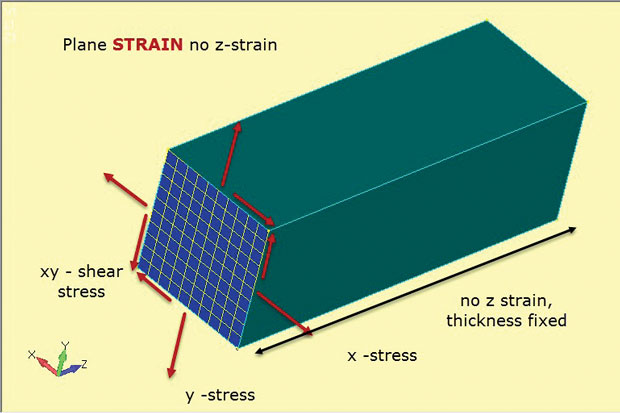Fig. 4: Planstam analys; stress och töjningstillstånd antaganden.

figuren visar orienteringen av 2D-Planets stamelement som ett snitt genom en typisk djup komponent. Antagandet är att spänningstillståndet vid denna snittdel kommer att dupliceras vid varje XY-planskärning (z-station) genom komponenten. Komponenten antas vara prismatisk (med ett konstant tvärsnitt) längs dess längd.

i praktiken använder vi denna metod där spänningstillståndet varierar långsamt från plan till plan i en djup komponent. Det bör finnas tillräckligt med material genom djup för att stabilisera och eliminera genom tjockleken stammen. Detta är samma princip som används på brottseghetsprover som visas i Fig. 5. Ett fel under plana töjningsförhållanden visas för mittdelen av det tjocka provet. Felet vid de fria kanterna och den tunna sektionen är ett annat läge, mer som ett planspänningstillstånd. En planstam FEA-modell skulle per definition vara en bra representation av mittlinjen tjockt provbeteende, men inte av de fria kanterna eller det tunna provet.

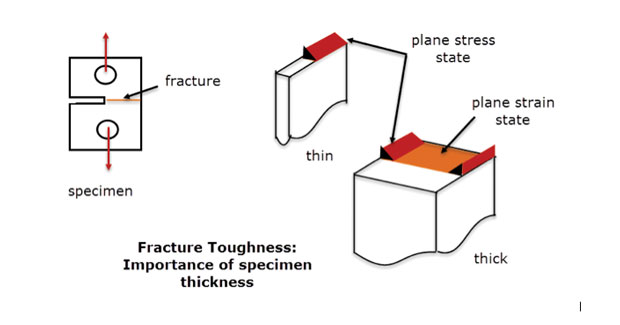Fig. 5: Brottseghetsprover; tunna och tjocka sektioner.

Fig. 6 visar en annan komponent som används i en kompositstruktur, som bildar en bunden Fog. Här är sektionen konstant och tillräckligt djup så att vi kan anta att spänningarna också är konstanta med djupet. De fria ändytorna (vid + z, – z) Kommer att ha ett annat lokalt spänningstillstånd (faktiskt planspänning, som noterat), men syftet med denna analys är att kontrollera nätsektionsspänningarna på mittlinjen (z = 0).

2D-Planets stamanalysnät visas sektionerat i 3D-komponenten i Fig. 7. Sektionsskärningen definieras vid station z = 0.

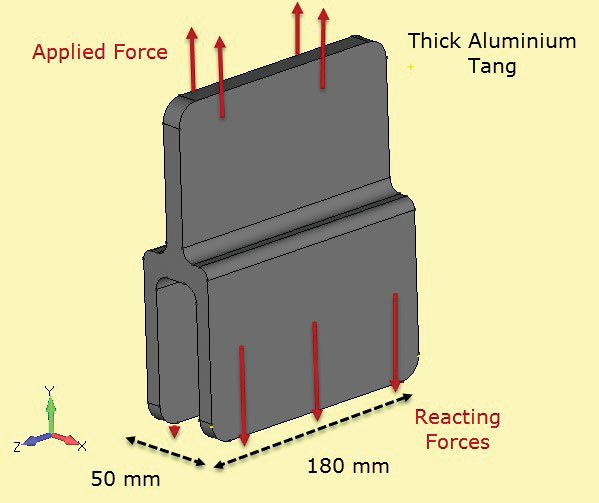Fig 6: djup sektion aluminium tang.

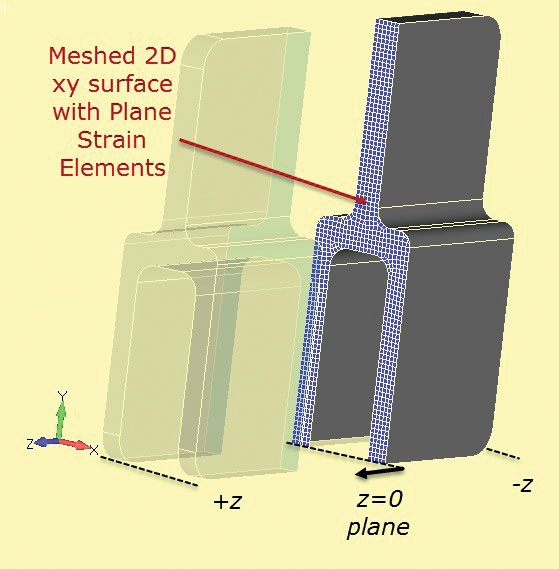Fig. 7: Avsnitt skär genom fast avsnitt för att utveckla 2D plan stam avsnitt.

en mycket fin 2D plan stam mesh kan användas, som kommer att köras mycket snabbt jämfört med en full 3D-modell. 2-1-begränsningsmetoden används som tidigare. Lastningen måste övervägas noggrant. ”Tjockleken” på planstammen är ganska godtycklig och är vanligtvis inställd på 1,0 som standard. Om belastningen på komponenten beräknas som en löpande belastning genom djup (N/m, Lbf/tum etc.) då kan detta värde användas direkt på planetspänningsnätet. Det är användbart att välja ett avsnitt, till exempel den enda tang och uppskatta den nominella eller genomsnittliga spänningen i det här avsnittet för hela komponenten. Detta kan användas som en sanity kontroll i planet stam analys. Felaktig laddning är förmodligen den främsta orsaken till fel i den här metoden.

resultaten av analysen visas i Fig. 8 och visa tydligt regionerna med hög stress runt axelfileten. Spänningarna gäller för komponentens centrala djupregion (z = 0).

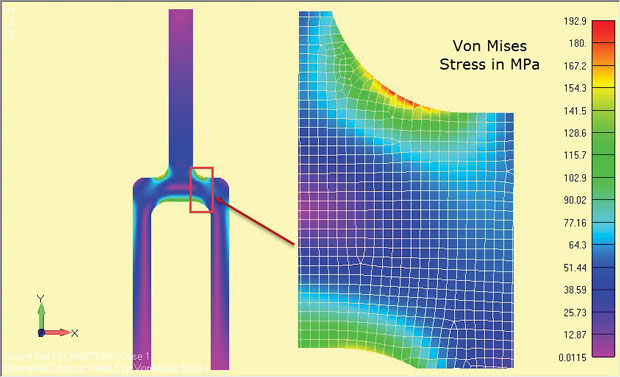Fig. 8: Planstam analysresultat av en djup tang komponent.

de spänningsmängder som används beror på vilken lösare som används. Vissa lösare ignorerar Z-riktningsspänningarna som sekundära och återställer spänningarna i planet. De huvudsakliga spänningarna och von Mises-spänningarna relaterar sedan till ett 2D-spänningstillstånd i planet. Om Z-riktningsspänningen återvinns bör den tydligt identifieras, så att 2D-spänningstillståndet i xy-planet kan identifieras.

vad exakt representerar z-riktningsspänningen? Det är den stress som utvecklats på grund av verkställigheten av noll z-riktningsstam. Spänningen fungerar som om de fria ändytorna på den prismatiska sektionen fixades. Vid det centrala planet för en djup sektionskomponent kommer dessa att vara de komplementära spänningarna som behövs för att hålla noll Z-riktningens spänningstillstånd. I verkligheten när vi rör oss mot de fria ytytorna sjunker z-spänningen till noll och blir en planspänningsfördelning (som ses i det tjocka sprickmekanikprovet).

i många fall, såsom en tryckcylinder, är ändytorna täckta och kommer faktiskt att utveckla en axiell spänning på grund av axiella krafter. Detta kommer att vara en annan spänning än den inducerade axiella spänningen i planbelastningsanalysen. En handberäkning kommer att behövas för att beräkna axiella spänningar, eller eventuellt en kompletterande axisymmetrisk modell för tryckkärl.

enkelheten i geometri och nätkonstruktion lämpar sig väl för ”vad-om” – studier eller mer formella formoptimeringsstudier.

för jämförelse gjordes en halv symmetri full 3D-analys av deep tang-komponenten och resultaten visas i Fig. 9. Den nominella spänningen över det övre enda tangbenet är identiskt i båda fallen—kom ihåg att detta är grunden för varje sanitetskontroll.

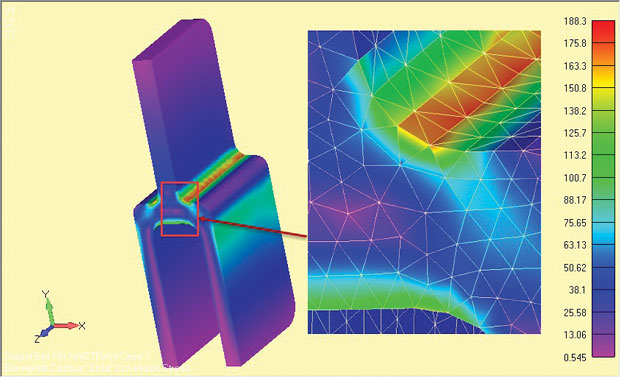Fig. 9: Full 3D-modell av deep tang, som visar stressresultat.

de lokala axelspänningarna är lägre med en liten procentandel i hela modellen. Detta är av tre skäl. För det första är det relativt grova 3D tet-nätet sämre än det mycket fina 2D-Planets lokala nät. En konvergenskontroll av 3D-modellen har inte genomförts.

för det andra är det en liten förändring i geometri vid de fria ytorna (+z,- z) jämfört med Z = 0-sektionen på grund av ändfileten. I detta fall är effekten försumbar eftersom fileten är borta från axelregionerna. I många komponenter kommer det dock att finnas lokala fileter och ta slut detaljer. vilket kommer att variera geometrin från en enkel XY plan yta. Lokala stressvariationer vid Fria ändytor kan behöva uppskattas eller kontrolleras med en full 3D-modell.

slutligen gäller inte antagandet av en fast z-begränsning vid + z,-z-sektioner för en ändlig djupkomponent. Z-spänningen kommer att diffundera till noll vid de ”riktiga” fria ansikten. Denna effekt visas i Fig. 10, som använder 3D-modellen som den är och även som en simulering av planet stam z stress.

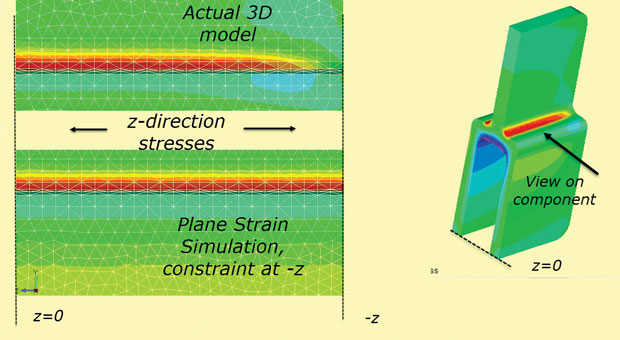Fig. 10: Diffusion av z-stress mot den fria ytan.

snabb och effektiv

plan stress och plan stam analyser är användbara 2D-metoder som ofta kan komplettera fullskaliga 3D-modeller. Inte alla funktioner kan representeras, men med viss uppfinningsrikedom kan spänningar på nyckelområden åtminstone uppskattas. Motivationen för att använda metoderna är att möjliggöra snabb effektiv analys med enkel 2D-geometri och nätkonstruktion.