Lär OpenCV

i det här inlägget kommer vi att lära oss detaljerna i histogrammet för orienterade gradienter (HOG) funktionsbeskrivare. Vi lär oss vad som finns under huven och hur denna deskriptor beräknas internt av OpenCV, MATLAB och andra paket.

detta inlägg är en del av en serie jag skriver om bildigenkänning och objektdetektering.

den fullständiga listan över handledning i denna serie ges nedan:

1. bildigenkänning med traditionella Datorsynstekniker : Del 1
2. Histogram av orienterade gradienter : del 2
3. exempelkod för bildigenkänning : del 3
4. träna en bättre ögondetektor: del 4a
5. objektdetektering med traditionella Datorsynstekniker : del 4b
6. hur man tränar och testar din egen OpenCV-objektdetektor : Del 5
7. bildigenkänning med deep learning : Del 6
   • introduktion till neurala nätverk
   • förstå Feedforward neurala nätverk
   • bildigenkänning med hjälp av Konvolutionella neurala nätverk
8. objektdetektering med Deep Learning: Del 7

många många saker ser svåra och mystiska ut. Men när du tar dig tid att dekonstruera dem ersätts mysteriet med behärskning och det är vad vi är ute efter. Om du är nybörjare och finner datorsyn hårt och mystiskt, kom bara ihåg följande

F : Hur äter du en elefant ?
A : En bit i taget!

Vad är en Funktionsbeskrivare?

en funktionsbeskrivare är en representation av en bild eller en bild patch som förenklar bilden genom att extrahera användbar information och kasta bort främmande information.

vanligtvis konverterar en funktionsdeskriptor en bild med storleksbredd x höjd x 3 (kanaler ) till en funktionsvektor / array med längd n. när det gäller HOG-funktionsdeskriptorn är ingångsbilden av storlek 64 x 128 x 3 och utgångsfunktions vektorn är av längd 3780.

Tänk på att HOG descriptor kan beräknas för andra storlekar, men i det här inlägget håller jag mig till siffror som presenteras i originalpapperet så att du lätt kan förstå konceptet med ett konkret exempel.

allt detta låter bra, men vad är ” användbart ”och vad är” främmande”? För att definiera ” användbart ”måste vi veta vad det är” användbart ” för ? Det är uppenbart att funktionsvektorn inte är användbar för att visa bilden. Men det är mycket användbart för uppgifter som bildigenkänning och objektdetektering. Funktionsvektorn som produceras av dessa algoritmer när de matas in i en bildklassificeringsalgoritmer som Support Vector Machine (SVM) ger bra resultat.

men, vilka typer av” funktioner ” är användbara för klassificeringsuppgifter ? Låt oss diskutera denna punkt med ett exempel. Antag att vi vill bygga en objektdetektor som upptäcker knappar på skjortor och rockar.

en knapp är cirkulär ( kan se elliptisk ut i en bild ) och har vanligtvis några hål för sömnad. Du kan köra en kantdetektor på bilden av en knapp och enkelt berätta om det är en knapp genom att helt enkelt titta på kantbilden ensam. I detta fall är kantinformation” användbar ” och färginformation är inte. Dessutom måste funktionerna också ha diskriminerande kraft. Till exempel bör bra funktioner som extraheras från en bild kunna se skillnaden mellan knappar och andra cirkulära föremål som mynt och bildäck.

i HOG-funktionsbeskrivaren används fördelningen ( histogrammen ) av riktningar för gradienter ( orienterade gradienter ) som funktioner. Gradienter (X-och y-derivat ) av en bild är användbara eftersom storleken på gradienter är stor runt kanter och hörn ( regioner med abrupta intensitetsförändringar) och vi vet att kanter och hörn packar i mycket mer information om objektform än platta regioner.

hur man beräknar Histogram av orienterade gradienter ?

i det här avsnittet kommer vi att gå in på detaljerna för att beräkna HOG-funktionsbeskrivaren. För att illustrera varje steg använder vi en patch av en bild.

Steg 1 : Förbehandling

som tidigare nämnts HOG feature deskriptor som används för fotgängare upptäckt beräknas på en 64 msk 128 patch av en bild. Naturligtvis kan en bild vara av vilken storlek som helst. Vanligtvis patchar på flera skalor analyseras på många bildplatser. Den enda begränsningen är att patcharna som analyseras har ett fast bildförhållande. I vårt fall måste patcharna ha ett bildförhållande på 1: 2. De kan till exempel vara 100 200, 128 256 eller 1000 2000 men inte 101 205 205.

för att illustrera denna punkt har jag visat en stor bild av storlek 720 275 475. Vi har valt en lapp av storlek 100 200 200 för att beräkna vår HOG feature descriptor. Denna patch beskärs ut ur en bild och storleksändras till 64 128. Nu är vi redo att beräkna SVINBESKRIVAREN för den här bildplåstret.

papperet av Dalal och Triggs nämner också gammakorrigering som ett förbehandlingssteg, men prestationsvinsterna är mindre och så hoppar vi över steget.

steg 2: Beräkna Gradientbilderna

för att beräkna en HOG-deskriptor måste vi först beräkna de horisontella och vertikala gradienterna; när allt kommer omkring vill vi beräkna histogrammet av gradienter. Detta uppnås enkelt genom att filtrera bilden med följande kärnor.

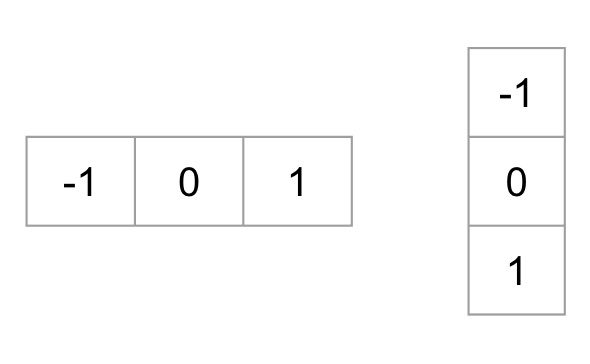
vi kan också uppnå samma resultat genom att använda sobel operator i OpenCV med kärnstorlek 1.

// C++ gradient calculation.// Read imageMat img = imread("bolt.png");img.convertTo(img, CV_32F, 1/255.0);// Calculate gradients gx, gyMat gx, gy;Sobel(img, gx, CV_32F, 1, 0, 1);Sobel(img, gy, CV_32F, 0, 1, 1);

# Python gradient calculation # Read imageim = cv2.imread('bolt.png')im = np.float32(im) / 255.0# Calculate gradientgx = cv2.Sobel(img, cv2.CV_32F, 1, 0, ksize=1)gy = cv2.Sobel(img, cv2.CV_32F, 0, 1, ksize=1)

därefter kan vi hitta gradientens storlek och riktning med hjälp av följande formel

om du använder OpenCV kan beräkningen göras med funktionen cartToPolar som visas nedan.

// C++ Calculate gradient magnitude and direction (in degrees)Mat mag, angle;cartToPolar(gx, gy, mag, angle, 1);

samma kod i python ser ut så här.

# Python Calculate gradient magnitude and direction ( in degrees )mag, angle = cv2.cartToPolar(gx, gy, angleInDegrees=True)

figuren nedan visar gradienterna.

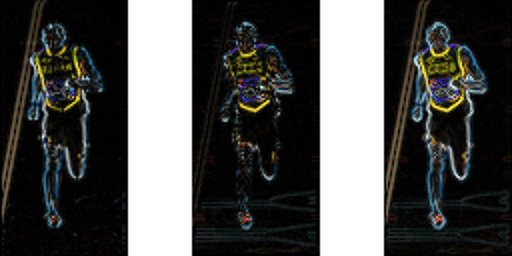
Observera att x-gradienten brinner på vertikala linjer och y-gradienten brinner på horisontella linjer. Storleken på lutning bränder där allt det finns en kraftig förändring i intensitet. Ingen av dem brinner när regionen är slät. Jag har medvetet utelämnat bilden som visar lutningsriktningen eftersom riktningen som visas som en bild inte förmedlar mycket.

gradientbilden tog bort mycket icke-väsentlig information ( t.ex. konstant färgad bakgrund ), men markerade konturer. Med andra ord kan du titta på lutningsbilden och ändå lätt säga att det finns en person på bilden.

vid varje pixel har lutningen en storlek och en riktning. För färgbilder utvärderas gradienterna för de tre kanalerna ( som visas i figuren ovan ). Storleken på gradienten vid en pixel är det maximala av storleken på gradienterna för de tre kanalerna, och vinkeln är vinkeln som motsvarar den maximala gradienten.

steg 3: Beräkna Histogram över gradienter i 8 8 celler

i detta steg är bilden uppdelad i 8 8-celler i 8-celler och ett histogram av gradienter beräknas för varje 8 8-celler i 8-celler.

vi kommer att lära oss om histogrammen på ett ögonblick, men innan vi åker dit, låt oss först förstå varför vi har delat bilden i 8 8-celler. En av de viktiga anledningarna till att använda en funktionsbeskrivare för att beskriva en patch av en bild är att den ger en kompakt representation. En 8-bild patch för 8-bild innehåller 8x8x3 = 192 pixelvärden. Lutningen av denna patch innehåller 2 värden ( magnitud och riktning ) per pixel som lägger till upp till 8x8x2 = 128 siffror.

i slutet av detta avsnitt kommer vi att se hur dessa 128 siffror representeras med ett 9-bin histogram som kan lagras som en matris med 9 siffror. Inte bara är representationen mer kompakt, beräkning av ett histogram över en patch gör denna representation mer robust för brus. Enskilda graidents kan ha buller, men ett histogram över 8 msk 8 patch gör representationen mycket mindre känslig för buller.

men varför 8 msk 8 patch ? Varför inte 32 32-32 ? Det är ett designval som informeras av omfattningen av funktioner vi letar efter. HOG användes initialt för fotgängardetektering. 8 msk 8 celler i ett foto av en fotgängare skalas till 64 msk 128 är tillräckligt stora för att fånga intressanta funktioner ( t.ex. ansiktet, toppen av huvudet etc. ).

histogrammet är i huvudsak en vektor (eller en array ) med 9 fack (siffror ) som motsvarar vinklar 0, 20, 40, 60 … 160.

Låt oss titta på en 8 msk 8 patch i bilden och se hur gradienterna ser ut.

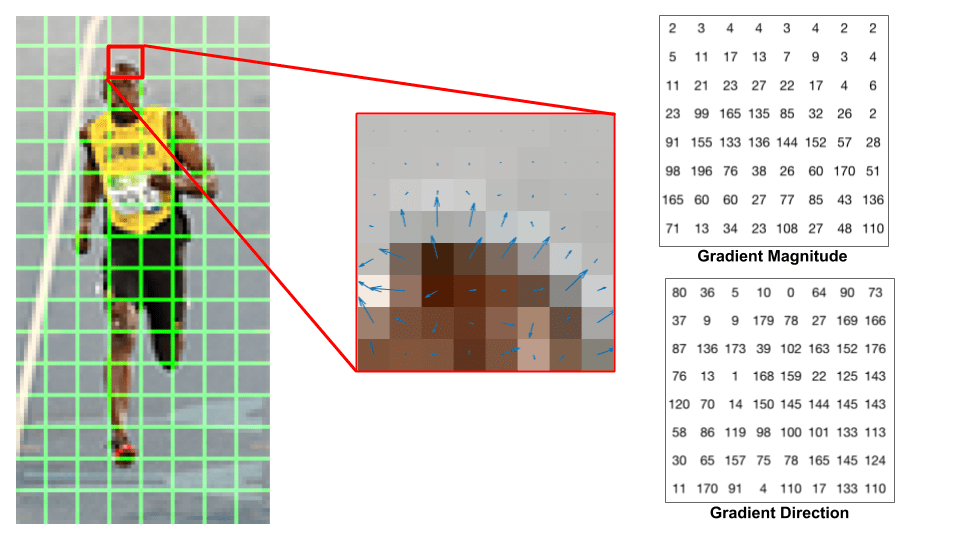
om du är nybörjare i datorsyn är bilden i mitten mycket informativ. Den visar plåstret på bilden överlagd med pilar som visar lutningen-pilen visar lutningsriktningen och dess längd visar storleken. Lägg märke till hur pilarnas riktning pekar på förändringsriktningen i intensitet och storleken visar hur stor skillnaden är.

till höger ser vi de råa siffrorna som representerar gradienterna i 8 — 8-cellerna med en mindre skillnad-vinklarna är mellan 0 och 180 grader istället för 0 till 360 grader. Dessa kallas ”osignerade” gradienter eftersom en gradient och den är negativ representeras av samma siffror. Med andra ord anses en lutningspil och den 180 grader motsatt den vara densamma. Men varför inte använda 0-360 grader ?

empiriskt har det visat sig att osignerade lutningar fungerar bättre än signerade lutningar för fotgängardetektering. Vissa implementeringar av HOG låter dig ange om du vill använda signerade gradienter.

nästa steg är att skapa ett histogram över gradienter i dessa 8-celler i 8-celler. Histogrammet innehåller 9 fack som motsvarar vinklarna 0, 20, 40 … 160. Följande figur illustrerar processen. Vi tittar på storleken och riktningen av gradienten av samma 8-8-lapp som i föregående figur.

ett fack väljs baserat på riktningen och rösten ( värdet som går in i facket ) väljs baserat på storleken. Låt oss först fokusera på pixeln omgiven i blått. Den har en vinkel (riktning ) på 80 grader och storleken på 2. Så det lägger till 2 till 5: e facket. Gradienten vid pixeln omgiven med rött har en vinkel på 10 grader och magnitud på 4. Eftersom 10 grader är halvvägs mellan 0 och 20 delas rösten av pixeln jämnt i de två facken.

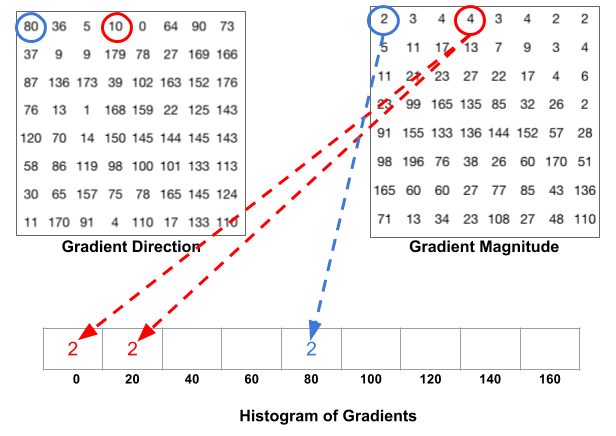
det finns ytterligare en detalj att vara medveten om. Om vinkeln är större än 160 grader är den mellan 160 och 180, och vi vet att vinkeln sveper runt vilket gör 0 och 180 ekvivalent. Så i exemplet nedan bidrar pixeln med vinkel 165 grader proportionellt till 0 graders bin och 160 graders bin.

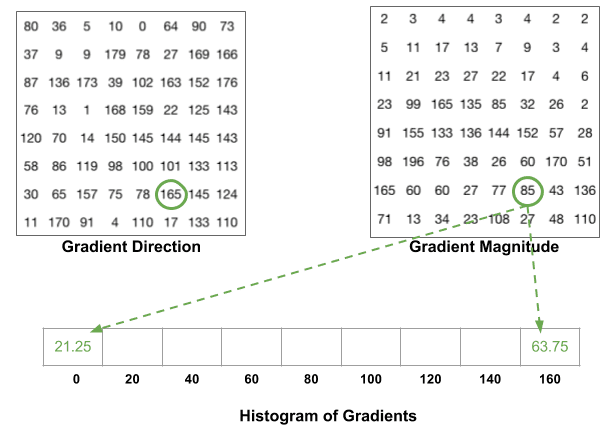
bidragen från alla pixlar i 8-cellerna i 8-celler läggs till för att skapa 9-bin-histogrammet. För plåstret ovan ser det ut så här

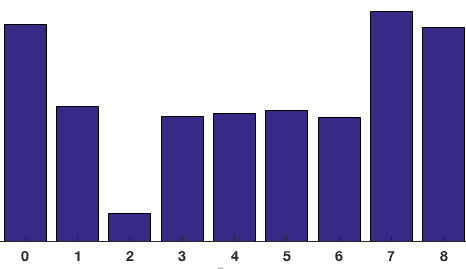
i vår representation är y-axeln 0 grader. Du kan se att histogrammet har mycket vikt nära 0 och 180 grader, vilket bara är ett annat sätt att säga att i patchgradienterna pekar antingen uppåt eller nedåt.

steg 4 : 16 msk 16 Block normalisering

i föregående steg skapade vi ett histogram baserat på bildens lutning. Gradienter av en bild är känsliga för övergripande belysning. Om du gör bilden mörkare genom att dela alla pixelvärden med 2, ändras gradientstorleken med hälften, och därför ändras histogramvärdena med hälften.

helst vill vi att vår deskriptor ska vara oberoende av belysningsvariationer. Med andra ord vill vi ”normalisera” histogrammet så att de inte påverkas av belysningsvariationer.

innan jag förklarar hur histogrammet normaliseras, låt oss se hur en vektor med Längd 3 normaliseras.

låt oss säga att vi har en RGB-färgvektor . Längden på denna vektor är $\sqrt{128^2 + 64^2 + 32^2} = 146.64$. Detta kallas också vektorns L2-norm. Att dela varje element i denna vektor med 146,64 ger oss en normaliserad vektor .

Tänk nu på en annan vektor där elementen är dubbelt så stora som den första vektorn 2 x = . Du kan träna det själv för att se att normalisering kommer att resultera i , vilket är detsamma som den normaliserade versionen av den ursprungliga RGB-vektorn. Du kan se att normalisering av en vektor tar bort skalan.

nu när vi vet hur man normaliserar en vektor, kan du bli frestad att tänka att när du beräknar HOG kan du helt enkelt normalisera 9 1-histogrammet på samma sätt som vi normaliserade 3 1-vektorn ovan. Det är inte en dålig ide, men en bättre IDE är att normalisera över en större storlek block av 16 16 xnumx xnumx xnumx xnumx xnumx xnumx xnumx xnumx xnumx xnumx.

ett 16 16-block har 4 histogram som kan sammanfogas för att bilda en 36 x 1-elementvektor och det kan normaliseras precis som en 3 1-vektor normaliseras. Fönstret flyttas sedan med 8 pixlar (se animering ) och en normaliserad 36 1-vektorvektor beräknas över det här fönstret och processen upprepas.

Steg 5: beräkna HOG feature vector

för att beräkna den slutliga funktionsvektorn för hela bildplåstret sammanfogas de 36 1-vektorerna till en jättevektor. Vad är storleken på denna vektor ? Låt oss beräkna

1. hur många positioner i 16-16-blocken har vi ? Det finns 7 horisontella och 15 vertikala positioner vilket gör totalt 7 x 15 = 105 positioner.
2. varje 16-block i 16-format representeras av en 36-vektor i 1-format. Så när vi sammanfogar dem alla i en gaintvektor får vi en 36 205 = 3780 dimensionell vektor.

visualisera Histogram av orienterade gradienter

HOG-deskriptorn för en bildplåster visualiseras vanligtvis genom att plotta de 9 1-normaliserade histogrammen i 8 8-cellerna. Se bild på sidan. Du kommer att märka att histogrammets dominerande riktning fångar personens form, särskilt runt torso och ben.

tyvärr finns det inget enkelt sätt att visualisera HOG descriptor i OpenCV.

Prenumerera & Ladda Ner Kod