jag har börjat göra Andrew ngs populära maskininlärningskurs på Coursera. Den första veckan täcker mycket, åtminstone för någon som inte har berört mycket kalkyl i några år
- Kostnadsfunktioner (genomsnittlig skillnad i kvadrat)
- Gradient nedstigning
- linjär Regression
dessa tre ämnen var mycket att ta in. Jag ska prata om var och en i detalj, och hur de alla passar ihop, med lite python-kod att demonstrera.
redigera 4 maj: Jag publicerade en uppföljning med fokus på hur kostnadsfunktionen fungerar här, inklusive en intuition, hur man beräknar den för hand och två olika Python-implementeringar. Jag kan göra gradient nedstigning och sedan föra dem samman för linjär regression snart.
Modellrepresentation
för det första är målet för de flesta maskininlärningsalgoritmer att konstruera en modell: en hypotes som kan användas för att uppskatta Y baserat på X. hypotesen eller modellen kartlägger ingångar till utgångar. Så, till exempel, säg att jag tränar en modell baserad på en massa bostadsdata som inkluderar storleken på huset och försäljningspriset. Genom att träna en modell kan jag ge dig en uppskattning av hur mycket du kan sälja ditt hus för baserat på dess storlek. Detta är ett exempel på ett regressionsproblem — med tanke på viss inmatning vill vi förutsäga en kontinuerlig utgång.
hypotesen presenteras vanligtvis som

Theta-värdena är parametrarna.
några snabba exempel på hur vi visualiserar hypotesen:
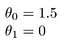
detta ger h (x) = 1,5 + 0x. 0x betyder ingen lutning, och y kommer alltid att vara konstant 1.5. Det här ser ut som:

vad sägs om
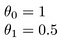

målet med att skapa en modell är att välja parametrar, eller theta-värden, så att h(x) är nära y för träningsdata, x och y. Så för dessa data
x =
y =

jag kommer att försöka hitta en linje med bästa passform med linjär regression. Nu sätter vi igång.
kostnadsfunktion
vi behöver en funktion som minimerar parametrarna över vår dataset. En vanlig funktion som ofta används är medelkvadratfel, som mäter skillnaden mellan uppskattaren (datauppsättningen) och det uppskattade värdet (förutsägelsen). Det ser ut så här:

det visar sig att vi kan justera ekvationen lite för att göra beräkningen nerför spåret lite enklare. Vi slutar med:
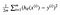
Låt oss tillämpa denna const-funktion på följande data:

för tillfället kommer vi att beräkna några theta-värden och plotta kostnadsfunktionen för hand. Eftersom denna funktion passerar genom (0, 0) tittar vi bara på ett enda värde av theta. Från och med nu kommer jag att hänvisa till kostnadsfunktionen som J (Brasilien).
för J(1) får vi 0. Ingen överraskning-ett värde på J (1) ger en rak linje som passar data perfekt. Vad sägs om J (0.5)?

MSE-funktionen ger oss ett värde på 0, 58. Låt oss plotta båda våra värden hittills:
J(1) = 0
J (0,5) = 0.58

jag ska gå vidare och beräkna några fler värden på J (GHz).

och om vi går ihop prickarna snyggt…

vi kan se att kostnadsfunktionen är minst när theta = 1. Det är vettigt-våra initiala data är en rak linje med en lutning på 1 (den orange linjen i figuren ovan).
Gradient Descent
vi minimerade J(Xhamster) genom försök och fel ovan — bara försöker massor av värden och visuellt inspektera den resulterande grafen. Det måste finnas ett bättre sätt? Kö gradient nedstigning. Gradient nedstigning är en allmän funktion för att minimera en funktion, i detta fall den genomsnittliga kvadrerade Felkostnadsfunktionen.
Gradient Descent gör i princip bara vad vi gjorde för hand — ändra theta-värdena, eller parametrarna, bit för bit, tills vi förhoppningsvis kom fram till ett minimum.
vi börjar med att initiera theta0 och theta1 till två värden, säg 0 för båda och gå därifrån. Formellt är algoritmen följande:

där Bisexuell, alfa, är inlärningshastigheten, eller hur snabbt vi vill gå mot minimum. Om det är för stort kan vi dock överskrida.

sammanföra allt-linjär Regression
snabbt sammanfatta:
vi har en hypotes:

som vi behöver passa till våra träningsdata. Vi kan använda en kostnadsfunktion som betyder Kvadratfel:

som vi kan minimera med hjälp av gradient descent:

vilket leder oss till vår första maskininlärningsalgoritm, linjär regression. Den sista pusselbiten vi behöver lösa för att ha en fungerande linjär regressionsmodell är det partiella derivatet av kostnadsfunktionen:
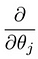
som visar sig vara:
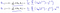
vilket ger oss linjär regression!
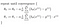
med teorin ur vägen fortsätter jag att implementera denna logik i python i nästa inlägg.
redigera 4 maj: jag publicerade en uppföljning med fokus på hur kostnadsfunktionen fungerar här, inklusive en intuition, hur man beräknar den för hand och två olika Python-implementeringar. Jag kan göra gradient nedstigning och sedan föra dem samman för linjär regression snart.