Simulerad glödgning för nybörjare

att hitta en optimal lösning för vissa optimeringsproblem kan vara en oerhört svår uppgift, ofta praktiskt taget omöjlig. Detta beror på att när ett problem blir tillräckligt stort måste vi söka igenom ett enormt antal möjliga lösningar för att hitta den optimala. Även med modern datorkraft finns det fortfarande ofta för många möjliga lösningar att överväga. I det här fallet eftersom vi inte realistiskt kan förvänta oss att hitta den optimala inom en förnuftig tid, måste vi nöja oss med något som är tillräckligt nära.
ett exempel på optimeringsproblem som vanligtvis har ett stort antal möjliga lösningar skulle vara problemet med resande säljare. För att hitta en lösning på ett problem som traveling salesman-problemet måste vi använda en algoritm som kan hitta en tillräckligt bra lösning på en rimlig tid. I en tidigare handledning tittade vi på hur vi kunde göra detta med genetiska algoritmer, och även om genetiska algoritmer är ett sätt vi kan hitta en ’tillräckligt bra’ lösning på resande säljare problem, det finns andra enklare algoritmer vi kan genomföra som också hittar oss en nära optimal lösning. I denna handledning algoritmen vi kommer att använda är, ’simulerad glödgning’.
om du inte är bekant med resande säljare problemet kan det vara värt att ta en titt på min tidigare handledning innan du fortsätter.

Vad är simulerad glödgning?

Låt oss först titta på hur simulerad glödgning fungerar, och varför det är bra att hitta lösningar på resande säljare problem i synnerhet. Den simulerade glödgningsalgoritmen inspirerades ursprungligen från glödgningsprocessen i metallarbete. Glödgning innebär uppvärmning och kylning av ett material för att ändra dess fysikaliska egenskaper på grund av förändringarna i dess inre struktur. När metallen svalnar blir dess nya struktur fixerad, vilket medför att metallen behåller sina nyligen erhållna egenskaper. Vid simulerad glödgning håller vi en temperaturvariabel för att simulera denna uppvärmningsprocess. Vi sätter det först högt och låter det långsamt ’svalna’ när algoritmen körs. Medan denna temperaturvariabel är hög kommer algoritmen att tillåtas, med mer frekvens, att acceptera lösningar som är sämre än vår nuvarande lösning. Detta ger algoritmen möjlighet att hoppa ut ur alla lokala optimum som den befinner sig i tidigt i körning. När temperaturen sänks så är chansen att acceptera sämre lösningar, vilket gör att algoritmen gradvis kan fokusera på ett område i sökutrymmet där förhoppningsvis en nära optimal lösning kan hittas. Denna gradvisa kylningsprocess är det som gör den simulerade glödgningsalgoritmen anmärkningsvärt effektiv för att hitta en nära optimal lösning när man hanterar stora problem som innehåller många lokala optimum. Den typ av resande säljare problemet gör det till ett perfekt exempel.

fördelar med simulerad glödgning

du kanske undrar om det finns någon verklig fördel med att implementera simulerad glödgning över något som en enkel bergsklättrare. Även om bergsklättrare kan vara förvånansvärt effektiva för att hitta en bra lösning, har de också en tendens att fastna i lokala optimum. Som vi tidigare bestämt är den simulerade glödgningsalgoritmen utmärkt för att undvika detta problem och är i genomsnitt mycket bättre på att hitta ett ungefärligt globalt optimalt.
för att bättre förstå låt oss snabbt ta en titt på varför en grundläggande hill climbing algoritm är så benägna att fastna i lokala optimum.
en hill climber-algoritm accepterar helt enkelt grannlösningar som är bättre än den nuvarande lösningen. När bergsklättraren inte hittar några bättre grannar stannar den.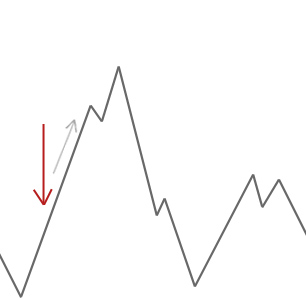

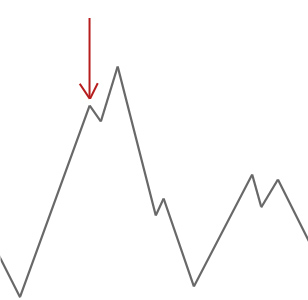
i exemplet ovan börjar vi vår bergsklättrare vid den röda pilen och den arbetar sig uppför backen tills den når en punkt där den inte kan klättra högre utan att först gå ner. I det här exemplet kan vi tydligt se att det sitter fast i ett lokalt optimum. Om detta var ett verkligt världsproblem skulle vi inte veta hur sökutrymmet ser ut så tyvärr skulle vi inte kunna berätta om den här lösningen är någonstans nära ett globalt optimalt.
simulerad glödgning fungerar något annorlunda än detta och kommer ibland att acceptera sämre lösningar. Denna egenskap hos simulerad glödgning hjälper den att hoppa ut ur alla lokala optimum som den annars skulle ha fastnat i.

Acceptansfunktion

Låt oss ta en titt på hur algoritmen bestämmer vilka lösningar som ska accepteras så att vi bättre kan förstå hur den kan undvika dessa lokala optimum.
först kontrollerar vi om grannlösningen är bättre än vår nuvarande lösning. Om det är så accepterar vi det villkorslöst. Men om grannlösningen inte är bättre måste vi överväga ett par faktorer. För det första, hur mycket sämre grannlösningen är, och för det andra, hur hög den nuvarande ’temperaturen’ i vårt system är. Vid höga temperaturer systemet är mer sannolikt Acceptera lösningar som är sämre.
matematiken för detta är ganska enkel:

i grund och botten är ju mindre energiförändringen (lösningens kvalitet) och ju högre temperaturen desto mer sannolikt är det för algoritmen att acceptera lösningen.

algoritm översikt

så hur ser algoritmen ut? Tja, i sin mest grundläggande implementering är det ganska enkelt.

• först måste vi ställa in den ursprungliga temperaturen och skapa en slumpmässig initial lösning.
• sedan börjar vi looping tills vårt stoppvillkor är uppfyllt. Vanligtvis har systemet tillräckligt kylt, eller en tillräckligt bra lösning har hittats.
• härifrån väljer vi en granne genom att göra en liten förändring av vår nuvarande lösning.
• vi bestämmer sedan om vi ska flytta till den grannlösningen.
• slutligen sänker vi temperaturen och fortsätter looping

Temperaturinitiering

för bättre optimering bör vi vid initiering av temperaturvariabeln välja en temperatur som initialt möjliggör praktiskt taget alla rörelser mot den aktuella lösningen. Detta ger algoritmen möjlighet att bättre utforska hela sökutrymmet innan kylning och bosättning i en mer fokuserad region.

exempelkod

låt oss nu använda det vi vet för att skapa en grundläggande simulerad glödgningsalgoritm och sedan tillämpa den på resande säljare problemet nedan. Vi kommer att använda Java i denna handledning, men logiken bör förhoppningsvis vara enkel nog att kopiera till valfritt språk.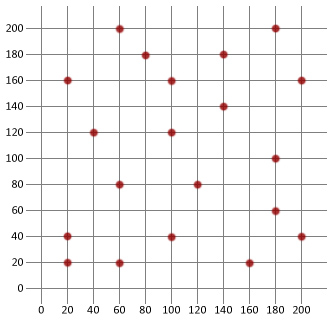

först måste vi skapa en Stadsklass som kan användas för att modellera de olika destinationerna för vår resande säljare.
Stad.java

nästa låt oss skapa en klass som kan hålla reda på städerna.
TourManager.java

nu för att skapa den klass som kan modellera en resande försäljare tour.
tur.java

slutligen, låt oss skapa vår simulerade glödgningsalgoritm.
Simuleradannealing.java

utgång

slutsats

i det här exemplet kunde vi mer än halva avståndet för vår ursprungliga slumpmässigt genererade rutt. Detta visar förhoppningsvis hur praktiskt denna relativt enkla algoritm är när den tillämpas på vissa typer av optimeringsproblem.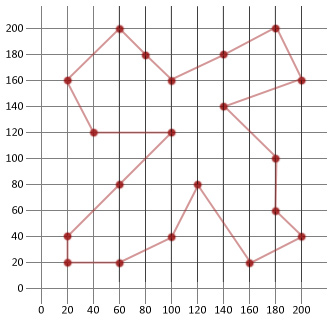

författare

Hej, Jag är Lee.
jag är en utvecklare från Storbritannien som älskar teknik och affärer. Här hittar du artiklar och handledning om saker som intresserar mig. Om du vill anställa mig eller veta mer om mig gå över till min om mig sida