Värmeledningsförmåga

värmeledningsförmågan hos fasta ämnen är av annan art beroende på huruvida de är ledare eller inte. I dielektrikum utan fria elektriska laddningar överförs termisk energi av fononer. De kollektiva vibrationerna av atomer i kristallgitteret har formen av förskjutningsvågor, vars störning genererar vågpaket, dvs fononer. Förskjutningsvågorna medför fluktuationer av densitet som kan manifesteras som en variation av brytningsindex. Om vågorna passerar genom ett område där brytningsindexet skiljer sig från det genomsnittliga volymetriska värdet, kommer de efterföljande förskjutningsvågorna som bär energin av termisk rörelse att spridas.

spridningen är desto starkare, desto mer är atomernas maximala avvikelse från deras medelpositioner i gallret, dvs Ju högre T. Detta står för det experimentellt etablerade faktumet att värmeledningsförmågan hos kristalldielektrikum minskar vid ganska höga temperaturer: 2084>1/t (Figur 1).

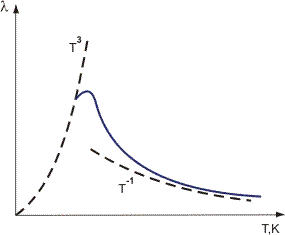
Figur 1. Variation av värmeledningsförmåga hos kristalldielektrikum med temperatur.

Debye gav en inblick i en toppliknande karaktär av variation i t vid låg T inom ramen för kvantmekaniska begrepp. Han utarbetade en dipolteori om dielektrikum baserat på begreppet en molekyl som en styv dipol. I denna modell introducerade Debye konceptet med den så kallade Debye-temperaturen oldd proportionell mot den maximala frekvensen av atomvibrationer i ett fast ämne. För de flesta ämnen är odrd antingen lägre än eller nära rumstemperaturen (ett undantag är diamant för vilken odrd = 1850 K och berrylium för vilken odrd = 1160k).

i kvantteorin för fasta ämnen betraktas kristallgitteret som en volym fylld med fonongas till vilken avdraget för den enklaste kinetiska teorin tillämpas

där c är värmekapaciteten hos en dielektrisk som sammanfaller med den för fonongas, v medelhastigheten för fononer ungefär lika med ljudhastigheten,den genomsnittliga fria vägen för fononer. Förekomsten av ett visst ändligt värde påär resultatet av fononspridning på fononer, på defekter av kristallgitter och i synnerhet på korngränser över hela provet. Temperaturberoendet för T(T) bestäms av och c på temperaturen.

vid höga temperaturer som väsentligt överstiger Debye-temperaturen oldd är den grundläggande mekanismen som begränsaren fonon-fononspridning på grund av anharmonicitet av atomvibrationer i en kristall. Phonon-phonon-mekanismen för termisk resistans ((1/kg) är känd som värmebeständighetskoefficienten) är endast möjlig på grund av en övergång som resulterar i retardation av fononflödet och märkbar förändring av kvasi-momentum. Ju högre T, desto högre är sannolikheten för övergången med minskande:(1/T). Eftersom vid t > ökar värmekapaciteten C endast något med temperaturen, följaktligen,1/T.

vid temperaturer som är lägre än Debye-temperaturen, t<<oldd, längden på den genomsnittliga fria vägenbestämd av phonon-phonon-spridningen växer drastiskt,exp oldd/T och är som regel begränsad till storleken på en kristall R. enligt Debye-lagen varierar värmekapaciteten c i detta temperaturområde som c(t/oldd)3. Följaktligen måste koefficienten för värmeledningsförmåga vid t 0 vid 0 minska i proportion till T3. Den temperatur för vilken värmeledningsförmågan har en topp bestäms från GHz r, vilket vanligen motsvarar t 0,05 xnumx xnumx xnumx xnumx xnumx xnumx xnumx xnumx xnumx.

denna teori redogör också för beteendet hos värmeledningskoefficienten för amorfa ämnen som inte har någon långdistansordning, dvs storleken på deras ”kristaller” är av storleksordningen atomstorlekar. På grund av detta måste spridning vid ”gränserna” för dessa ämnen råda vid alla T och bisexuell const. Värmekonduktivitetskoefficienten för amorfa ämnen är T3 vid låga temperaturer och måste växa något, i proportion till värmekapaciteten, vid måttliga och höga temperaturer, T > oldd.

allt detta ger en kvalitativ förklaring av beroendet av det verkliga kristall dielektrikum, men tar ingen hänsyn till avvikelser från det konstanta gitteret på grund av atomära föroreningar av andra element och deras egna isotoper. Vid hög temperatur är motståndet som erbjuds av föroreningar för värmetransport oberoende av temperaturen. Detta gör det möjligt att uppskatta graden av kristallrenhet från variation av dess värmeledningsförmåga med temperatur. Samma faktum gör det möjligt för oss att bestämma fördelningen mellan glasaktigt och kristallämne i det naturliga mineralet om glaset betraktas som en orenhet i en kristall.

värmeledningsförmåga i metaller beror på rörelse och interaktion mellan strömbärare, dvs ledningselektroner. I allmänhet, koefficienten för termisk ledningsförmåga (λ) av metall som motsvarar summan av gallret (phonon) λph, och elektron-λe komponenter, λ) = λe + λph; vid vanliga temperaturer, som regel, λe >>λph.

om vi tillämpar en enkel kinetisk teori om gaser på flödet av fria elektroner och antar att längden på deras fria väg inte beror på hastighet, innebär teorin att

där e är elektronladdningen, K Boltzrnanns konstant, och bisexuell den elektriska ledningsförmågan. En strikt kvantmekanisk teori erbjuder en liknande relation,

i båda formlerna verkar förhållandet mellan elektrondelen av värmekonduktivitetskoefficienten 2x till elektrisk ledningsförmåga 2x, i ett brett temperaturområde, vara i proportion till temperaturen enligt Wiedemann-Franz-lagen, 2XC/XC = LT, där L är Lorentz-numret. Denna lag används för att beräkna den uppmätta elektriska ledningsförmågan. Det bryts emellertid vid temperaturer under oc-d när en elektron-fononinteraktion råder (oc-d växer med minskande T som T-5 medan le varierar mer något som T-2).

de experimentella resultaten visar att värmeledningsförmågan hos metaller vid höga temperaturer i regel är en något minskande temperaturfunktion. Men det finns många undantag. Således minskar värmeledningsförmågan hos järn kraftigt med temperaturen medan tantal och niob visar en positiv temperaturkoefficient.

av intresse är försöken att jämföra koefficienterna för värmeledningsförmåga för olika ämnen för en enda karakteristisk temperatur, till exempel för smältpunkten Tm för fasta ämnen. Således har den statistiska behandlingen av experimentella data som utförts av Missenard visat att värmeledningsförmågan hos metaller vid smältpunkten Bisexuell(T = Tm) = Bisexuell står i proportion tilloch värmeledningsförmågan hos dielektriska kristaller vid T = Tm står i proportion till, där m är molekylmassan, n antalet atomer i den kemiska formeln, densitet för Kakor, och smältpunkten Tm är i Kelvin.

värmetransport i halvledare är mer komplex än i dielektrikum och metaller eftersom fononen och elektronkomponenterna är lika viktiga för dem. En annan orsak till komplexiteten är den avsevärda effekten av föroreningar, bipolär diffusion och andra lite studerade faktorer på värmeöverföring.

effekten av tryck på värmeledningsförmågan hos fasta ämnen kan antas, med god noggrannhet, att vara linjär, för många metaller som växer med p.

för effekten av porositet på värmeledningsförmågan hos fasta ämnen se poröst Medium.