SSIM blev først introduceret i IEEE-papiret fra 2004, Billedkvalitetsvurdering: fra Fejlsynlighed til strukturel lighed. Abstraktet giver en god intuition til ideen bag det foreslåede system,
objektive metoder til vurdering af perceptuel billedkvalitet forsøgte traditionelt at kvantificere synligheden af fejl (forskelle) mellem et forvrænget billede og et referencebillede ved hjælp af en række kendte egenskaber ved det menneskelige visuelle system. Under den antagelse, at menneskelig visuel opfattelse er meget tilpasset til at udtrække strukturel information fra en scene, introducerer vi en alternativ komplementær ramme for kvalitetsvurdering baseret på nedbrydning af strukturel information.
sammendrag: forfatterne gør 2 væsentlige punkter,
- de fleste billedkvalitetsvurderingsteknikker er afhængige af kvantificering af fejl mellem en reference og et prøvebillede. En almindelig metric er at kvantificere forskellen i værdierne for hver af de tilsvarende billedpunkter mellem prøven og referencebillederne (ved f.eks.
- det menneskelige visuelle opfattelsessystem er i høj grad i stand til at identificere strukturel information fra en scene og dermed identificere forskellene mellem Informationen ekstraheret fra en reference og en prøvescene. Derfor vil en metric, der replikerer denne adfærd, fungere bedre på opgaver, der involverer at skelne mellem en prøve og et referencebillede.
det strukturelle Lighedsindeks (SSIM) metriske udtrækker 3 nøglefunktioner fra et billede:
- luminans
- kontrast
- struktur
sammenligningen mellem de to billeder udføres på basis af disse 3 funktioner.
Fig 1 nedenfor viser arrangementet og strømmen af det strukturelle Lighedsmålesystem. Signal Y og Signal Y henviser til Reference-og prøvebillederne.

men hvad beregner denne måling?
dette system beregner det strukturelle Lighedsindeks mellem 2 givne billeder, som er en værdi mellem -1 og +1. En værdi på +1 indikerer, at de 2 givne billeder er meget ens eller de samme, mens en værdi på -1 indikerer, at de 2 givne billeder er meget forskellige. Ofte justeres disse værdier til at være i området, hvor ekstremerne har samme betydning.
lad os nu kort undersøge, hvordan disse funktioner er repræsenteret matematisk, og hvordan de bidrager til den endelige SSIM-score.
- luminans: luminans måles ved gennemsnit over alle billedværdier. Dens betegnet med Kurt (Mu) og formlen er angivet nedenfor,
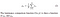
- Kontrast: Det måles ved at tage standardafvigelsen (kvadratroden af variansen) af alle billedværdierne. Det er betegnet med Kurt (Sigma) og repræsenteret ved nedenstående formel,
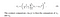
- Struktur: Den strukturelle sammenligning udføres ved hjælp af en konsolideret formel (mere om det senere), men i det væsentlige deler vi indgangssignalet med dets standardafvigelse, så resultatet har enhedsstandardafvigelse, som giver mulighed for en mere robust sammenligning.
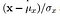
så nu har vi etableret den matematiske intuition bag de tre parametre. Men hold fast! Vi er endnu ikke færdige med matematikken, lidt mere. Hvad vi mangler nu, er sammenligningsfunktioner, der kan sammenligne de to givne billeder på disse parametre, og endelig en kombinationsfunktion, der kombinerer dem alle. Her definerer vi sammenligningsfunktionerne og endelig kombinationsfunktionen, der giver lighedsindeksværdien
- luminans sammenligningsfunktion: den er defineret af en funktion, l(H, y) som er vist nedenfor. (mu) repræsenterer middelværdien af et givet billede. Y og Y er de to billeder, der sammenlignes.
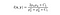
hvor C1 er en konstant for at sikre stabilitet, når nævneren bliver 0. C1 er givet af,
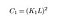
opdatering: i hele artiklen havde vi ikke undersøgt, hvad k-og L-konstanterne i denne ligning er. Heldigvis påpegede en læser det i kommentarerne, og så for at gøre denne artikel lidt mere nyttig, vil jeg bare definere dem her.
L er det dynamiske område for billedværdier (vi indstiller det som 255, da vi har at gøre med standard 8-bit billeder). Du kan læse mere om, hvad de forskellige billedtyper er, og hvad de betyder, her.
K1, K2 er bare normale konstanter, intet meget der!
- kontrast sammenligning funktion: det er defineret af en funktion c(H, y), som er vist nedenfor. den angiver standardafvigelsen for et givet billede. Y og Y er de to billeder, der sammenlignes.
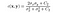
hvor C2 er givet af,
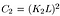
- struktur sammenligning funktion: det er defineret af funktionen s (H, y), som er vist nedenfor. den angiver standardafvigelsen for et givet billede. Y og Y er de to billeder, der sammenlignes.
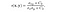
hvor L(S) er defineret som,
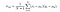
og endelig er SSIM score givet af,

hvor kr > 0, kr > 0, kr > 0 angiver den relative betydning af hver af målingerne. For at forenkle udtrykket, hvis vi antager, kan vi få, hvis vi går ud fra, at vi er = Kvit = kvit = 1 og C3 = Kvit/2,
men der er en plotvridning!
mens du ville være i stand til at implementere SSIM ved hjælp af ovenstående formler, er chancerne for, at det ikke vil være så godt som de tilgængelige klar-til-brug-implementeringer, som forfatterne forklarer det,
til vurdering af billedkvalitet er det nyttigt at anvende SSIM-indekset lokalt snarere end globalt. For det første er billedstatistiske funktioner normalt meget rumligt ikke-stationære. For det andet kan billedforvrængninger, som måske eller måske ikke afhænger af den lokale billedstatistik, også være rumvariant. For det tredje, ved typiske synsafstande, kan kun et lokalt område i billedet opfattes med høj opløsning af den menneskelige observatør ad gangen (på grund af HVS ‘ s foveationsfunktion ). Og endelig kan lokal kvalitetsmåling give et rumligt varierende kvalitetskort over billedet, som leverer mere information om kvalitetsforringelsen af billedet og kan være nyttigt i nogle applikationer.
sammendrag: I stedet for at anvende ovenstående målinger globalt (dvs.over hele billedet på en gang) er det bedre at anvende metrics regionalt (dvs. i små sektioner af billedet og tage gennemsnittet generelt).
denne metode kaldes ofte det gennemsnitlige strukturelle Lighedsindeks.
på grund af denne ændring i tilgang fortjener vores formler også ændringer for at afspejle det samme (det skal bemærkes, at denne tilgang er mere almindelig og vil blive brugt til at forklare koden).
(Bemærk: Hvis indholdet nedenfor virker lidt overvældende, ingen bekymringer! Hvis du får kernen i det, vil det at gå gennem koden give dig en meget klarere ide.)
forfatterne bruger en 11h11 cirkulær-symmetrisk Gaussisk vejefunktion (dybest set en 11h11-matrice, hvis værdier er afledt af en gaussisk fordeling), der bevæger sig punkt-for-punkt over hele billedet. Ved hvert trin beregnes den lokale statistik og SSIM-indekset inden for det lokale vindue. Da vi nu beregner metrics lokalt, revideres vores formler som,
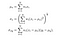
hvor vi er den gaussiske vægtningsfunktion.
hvis du fandt dette lidt uintuitivt, ingen bekymringer! Det er tilstrækkeligt at forestille sig vi som en multiplicand, der bruges til at beregne de krævede værdier ved hjælp af nogle matematiske tricks.
når beregninger er udført over hele billedet, tager vi simpelthen gennemsnittet af alle de lokale SSIM-værdier og når frem til den globale SSIM-værdi.
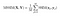
endelig færdig med teorien! Nu til koden!