den mest anvendte værdi i en jordrapport er sandsynligvis jordbærende kapacitet. Den åbenlyse årsag er, at grundlæggende eksempler i de fleste lærebøger næsten altid bruger bæreevne til at beregne plandimensionen på en fod. På grund af enkelhed og brugervenlighed er denne metode stadig den grundlæggende jordparameter til fundamentdesign. Imidlertid antager denne enkelhed, at fodfoden opfører sig som en stiv krop. Denne særlige antagelse fungerer godt i praksis for små og enkelt kolonne footings. Men for store og multi kolonne fundamenter foretrækker de fleste ingeniører fleksibel analyse. Manuel beregning af fleksibel analyse kan være udfordrende og i næsten alle tilfælde programmer som STAAD, SAFE, GT STRUDL osv. bruges. Imidlertid beder disse computerprogrammer ofte om et input kaldet “modulus of subgrade reaction”. Mange ingeniører er ikke bekendt med dette udtryk og forsøger ofte at sammenligne det med bæreevne. Da flere og flere ingeniører vil bruge programmel til at designe fundamenter, er det vigtigt for ingeniører at have en grundlæggende forståelse af denne jordparameter. Er der nogen sammenhæng mellem bæreevne og modulus af subgrade reaktion?
modulus of Subgrade Reaction (Ks)
dette udtryk måles og udtrykkes som belastningsintensitet pr. For det engelske enhedssystem udtrykkes det ofte i kip/in2/in; i SI-systemet udtrykkes det som kN/m2/m. nogle udtrykker dette udtryk i kip/in3 (eller kN / m3), som kan være vildledende. Numerisk er kip / in3 korrekt, men repræsenterer ikke korrekt den fysiske betydning af den målte værdi og kan forveksles som en densitetsenhed eller en volumetrisk måling.
matematisk udtrykkes koefficienten for subgrade reaktion som:
Ks = p/S (KVN 1)
hvor p = kontakttrykintensitet og S = jordafvikling
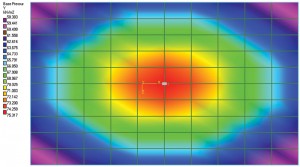
figur 1a: Afbøjningsdiagram og jordtrykskontur.
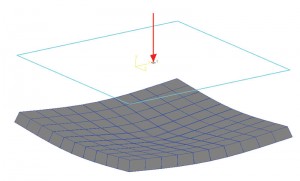
figur 1b: jordtrykskontur.
som nævnt kan korrekt estimering af kontakttryk for et fleksibelt fundament være meget besværligt, så det antages, at Ks forbliver konstant for hele foden. Med andre ord vil forholdet mellem tryk og afvikling på alle steder af en fod forblive konstant. Så forskydningsdiagrammet for en fod med en belastning i midten vil have en dishing effekt. Et punkt i midten af foden vil opleve den højeste forskydning. Forskydning reduceres, når den bevæger sig væk fra midten. Figur 1a viser en simpel plade-på-grade fundament. Det blev modelleret og analyseret i STAAD Foundation som “Mat”, som er et fleksibelt fundament; jorden blev defineret ved hjælp af koefficient for subgrade reaktion. Til denne øvelse blev programmets standardværdi for modulet for subgrade-reaktion anvendt. Forskydningsdiagrammet viser en dishing effekt som diskuteret tidligere. Figur 1b viser jordtrykskonturen. Det er også indlysende, at trykintensiteten i midten er maksimal og reduceres, når elementerne (eller knudekoordinaterne) bevæger sig væk fra midten. Så det kunne antages, at forholdet mellem trykintensitet og afvikling er konstant.
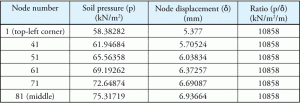
tabel 1: jordtryk, knudeforskydning og deres forhold.
overvej nogle af tallene fra det samme eksempel. Jordtryk, tilsvarende forskydning og forholdet er anført i tabel 1. Punkterne er repræsenteret på en diagonal for at illustrere variationen i tryk og forskydning, når punkterne bevæger sig væk fra midten til det fjerneste punkt i hjørnet af den rektangulære fod. Figur 2 viser punkterne på måttepladen.
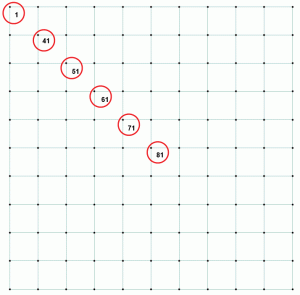
Figur 2: Udvalgte punkter til sammenligning af basistryk, afbøjning og forhold.
dette er næppe en overraskelse, da modulet for subgrade reaction (Ks) pr. Det er også vigtigt at bemærke, at programmets standard KS-værdi (10858 kN/m2/m) var nøjagtig den samme som det konstante forhold beregnet i tabel 1.
Basetryk blev beregnet ud fra understøtningsreaktionen. Man kunne tro, at forholdet mellem støtte reaktion og tilsvarende forskydning også vil være en konstant. Som vist i tabel 2 er forholdene ikke konstante for alle værdier. Hvordan bruges Ks-værdien inde i programmet, og hvordan beregnes basistrykket?
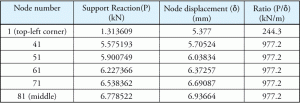
tabel 2: støtte reaktion og forskydning.
Biflodsområde
ofte antages det at beregne, hvor meget areal af en plade der kan tilskrives en knude eller med andre ord indflydelsen af hver knude på pladens overfladeareal. Det afhænger af pladens form. For en perfekt kvadratisk eller rektangulær plade, vil hver node påvirke præcis mast af pladens overfladeareal (figur 3a). Men for en generaliseret firkant ville den bedste praksis være at beregne midten af pladens masse og derefter tegne linjer fra det midterste punkt til midtpunkterne på hver side. I figur 3b repræsenterer det skraverede område indflydelsesoverfladearealet for den tilsvarende knude.
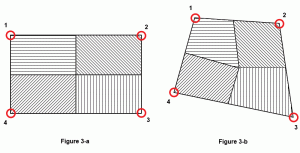
figur 3: knudepunkt.
Fjederstøttekonstant
den ovenfor beskrevne beregning af biflodsareal er den nøgleprocedure, der anvendes internt af det kommercielle program til beregning af den lineære fjederkonstant. Programmet beregner først biflodsområdet for hver fodknude og multiplicerer derefter modulet for subgrade reaktion med det tilsvarende biflodsområde for hver knude for at få den lineære fjederkonstant ved hver knude.
Kyi = KS Tai (EKN 2)
hvor
Kyi er fjederkonstanten ved ith-noden
Tai er indflydelsesområdet for ith-noden
Ks er modulet for subgrade-reaktion
for en konkret fundamentanalyse skal disse fjedre være i stand til at udføre en defineret som kun kompression, da beton antages ikke at bære nogen trækkraft. Basistrykket beregnes ved hver understøtningsknude ved at dividere understøtningsreaktionen med det tilsvarende knudepunkt biflodsområde. Hvis vi ser på ovenstående eksempel, har Node 1 et meget mindre biflodsområde end resten af knudepunkterne. Det kan også bemærkes, at alle andre knuder har samme biflodsområde. Dette forklarer tabel 2, da det viser forholdet for Node 1 er anderledes end andre noder. Figur 4 viser biflodsområdet for forskellige noder. Node 1 har et biflodsområde, som er 25% af Node 81. Tabel 3 er en udvidelse af tabel 1 og 2 og viser, hvordan konstant forhold opnås for alle noder.
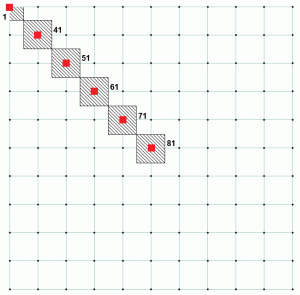
figur 4: Biflodsområde for udvalgte noder.
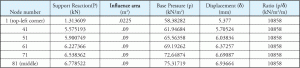
tabel 3: reaktion, basistryk, forskydning, KS konstant.
tilladt afvikling
bæreevne er måling af jordtrykket, som en jord sikkert kan bære. Med andre ord er bæreevne det tryk, som jorden kan modstå, før den svigter. De to vigtigste jordfejlkriterier er:
- Forskydningsfejl
- maksimal tilladt afvikling
blandt mange faktorer kan fundamentbredde (B) påvirke fejlkriterier. Normalt styrer forskydningsfejl for mindre fundamenter, og afviklingsfejl styrer større fundamenter. Tabel 4 er et typisk eksempel, der viser forholdet mellem forskellige fundamentstørrelser og fejlkriterier.
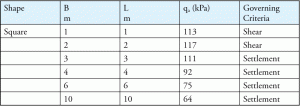
Tabel 4: Endelig tilladt bæreevne for tilladt afregning = 25 mm og en given indlejringsdybde.
for at estimere afviklingsfejl antages en tilladt afviklingsværdi (normalt 25 mm eller 1 tomme). Når jorden afregner mere end den tilladte værdi, fejler jorden. Så selv for en beregning af bæreevne anvendes en tilladt jordafvikling, og bygningsingeniører skal være opmærksomme på denne værdi, mens de designer en fod. Den tilladte jordafregningsværdi er typisk en integreret del af enhver jordrapport.
Hvorfor bruge modulet for Subgrade Reaction
det blev tidligere anført, at for at designe et fleksibelt matfundament anvendes modulet for subgrade reaction i stedet for jordens bæreevne. Men hvorfor? Svaret ligger i de underliggende antagelser om, hvordan et fundament kan opføre sig.
fundamenter kan være stive eller fleksible. Bæreevne bruges til at designe stive fundamenter, men undergradreaktion bruges til fleksible fundamenter. Selve antagelsen om et stift fundament er, at “fordelingen af undergradreaktionen p over fundamentets bund skal være plan, fordi et stift fundament forbliver plan, når det sætter sig.”Overvej en simpelthen understøttet stråle indlæst i midten, som vist i figur 5a. ved statik kan vi opnå R1 = P/2 og R2 = P/2. Hvis den samme stråle indlæses ekscentrisk, kan reaktionen beregnes som vist i figur 5b.
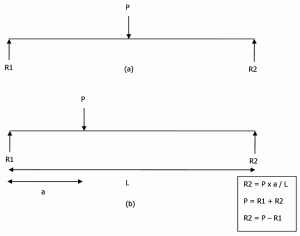
figur 5: Reaktioner for en simpelthen understøttet stråle.
det samme koncept udvides til stift fundamentdesign. Men i stedet for endestøtterne understøttes hele fundamentet. Det antages også, at betonpladens relative stivhed er meget højere end jordstivheden. Så antages pladen at forblive plan, selv efter påføring af belastning.
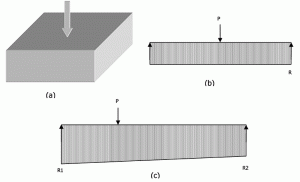
figur 6: Sub grade reaktioner for en isoleret fod.
figur 6a viser en fod, der er indlæst i midten. Fra en stiv bred stråleanalogi, P = R L. Tilsvarende for en ekscentrisk indlæst fod vil reaktionen variere lineært fra den ene ende til den anden som vist i figur 6c. ligninger 3 og 4 kan løses for at finde slutreaktioner. Men ingen af ligningerne indeholder modulus of subgrade reaction (Ks). Så “fordelingen af subgrade reaktion på bunden af en stiv fod er uafhængig af graden af kompressibilitet af den subgrade”, den hviler på. Som mange forfattere har konkluderet, kan et stift fundament designes sikkert ved hjælp af bæreevne, da denne metode i de fleste tilfælde giver mere konservative resultater.
P = 1/2l(R1 + R2) (EKN 3)
P = 1/6b2r1 + 1/3b2r2 (EKN 4)
men et matfundament er ofte designet som et fleksibelt fundament, da det kan være stort i størrelse, og der kan være mange belastningspunkter og andre kompleksiteter, herunder huller og bjælker. Udbredt tilgængelighed af FEA-programmer bidrager til denne tendens. Men i modsætning til stive fundamenter kan et fleksibelt fundament ikke have lineær undergradreaktion. Det afhænger snarere af fundamentets kompressibilitet såvel som den strukturelle stivhed. Et fleksibelt fundament udsættes for intern bøjning og relative forskydninger mellem to pladepunkter. Jo større strukturel stivhed, desto mindre er den relative forskydning. Forfatteren testede sagen med meget høj stivhed af pladeelementerne, hvilket resulterede i en næsten plan overflade efter påføring af belastningen. Tilsvarende, jo større modul for subgrade reaktion, jo mindre er trykfordelingen. Med andre ord vil en højere KS-værdi absorbere mere tryk ved belastningspåføringspunktet. Derfor anvendes modulet for subgrade reaktion,som er funktionen af jordafvikling og det ydre tryk, til fleksibelt fundamentdesign.
korrelationer
det mest almindelige – og sandsynligvis det sikreste – svar på spørgsmålet om sammenhæng mellem bæreevne og modulet for subgrade reaktion er, at der ikke er nogen sammenhæng. Men der skal være en, da begge er målinger af jordkapacitet, og en af disse to parametre kan bruges til at designe et regelmæssigt fundament.
igen er definitionen af Ks trykket pr. Med andre ord, jord kapacitet til at modstå tryk for en given forskydning. Fra tidligere diskussioner er det også klart, at selv bæreevne har en tilladt afvikling. Det er derfor fristende at konkludere, at modulet for subgrade reaktion er bæreevne pr.
denne konklusion ligner meget ligningen præsenteret af kasser.
SI: Ks = 40 (SF)kvalitet kn/m3(miljø 5)
FPS: Ks = 12 (SF)kvalitet k/ft3 (miljø 6)
hvor SF = sikkerhedsfaktor og kvalitet er den tilladte bæreevne.
i ligninger 5 og 6 konverteres den tilladte bæreevne først til den ultimative bæreevne ved at multiplicere med en sikkerhedsfaktor. Forfatteren antog en tomme eller 25 mm afvikling. Den endelige ligning formuleres derefter dividere den ultimative bæreevne af den antagne afvikling.
den mere generiske form af ligningen kan skrives som:
Ks = 
stress/forskydning (EKN 7)
hvor
i = sikkerhedsfaktor
kvalitet er den tilladte bæreevne
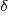er den tilladte jordafvikling
disse ligninger viser tydeligt, at den passende sikkerhedsfaktor skal anvendes, og Ks-værdien kan sammenlignes bedre med den ultimative bæreevne snarere end den tilladte bæreevne. Sikkerhedsfaktoren kan variere afhængigt af projekter og geotekniske ingeniører. Den anden vigtige faktor er den antagne tilladte afregning for den beregnede bæreevne.
det skal ligeledes bemærkes, at de basistrykværdier, der indberettes ved FEA-analyse, ikke kan sammenlignes direkte med bæreevne. Det maksimale basistryk multipliceres med sikkerhedsfaktoren og sammenlignes derefter med jordens tilladte bæreevne.
men de ovennævnte ligninger har begrænsninger. De kan anvendes på footings, hvor afviklingsfejl regulerer, men kan ikke relateres til footings, hvor forskydningsfejl opstår, før den tilladte afviklingsgrænse nås. Så ingeniører skal udvise forsigtighed, før de bruger disse ligninger.
konklusion
sammenhængen mellem bæreevne og modul for subgrade reaktion er i bedste fald et skøn. Det kan bruges til estimering, men en Ks-værdi bestemt ved en pladebelastningstest skal altid bruges, hvis den er tilgængelig eller skal anmodes om, når det er muligt. Ovenstående diskussion giver imidlertid indsigt i disse værdier og hjælper ingeniører med at forstå den fysiske betydning af modul for subgrade reaktion. Og, som altid, bygningsingeniører bør konsultere en geoteknisk ingeniør professionel inden færdiggørelse af jordstivhed og bærende værdier.▪