Husholder Transformation
Husholder Transformation (også “Husholder refleksion”) er en ortogonal refleksion transformation:
- det reflekterer vektorerne i søjlerne i matricen, således at
- den første vektor har alle nuller undtagen det første element
Transformationsmatricen
Refleksionstransformation:
egenskaber
Husholder matricer er symmetriske og ortogonale: de er refleksionsmatricer
afledning
så vi har $P = I – 2VV^t$:
vi bruger sådanne transformationer til nulstilling af elementer
som i tilfælde af LU-nedbrydning, hvor vi anvendte en række Gauss-transformationsændringer, kan vi gøre det samme og udføre en række Husholdertransformationer
- så hvis vi vælger $y = \pm e_1$ (hvor $e_1$ er matricen med 1 på position 1 og hvile er nuller)
- så vil det nul alle elementer på $$ undtagen den første
- således ved det passende valg af $H$ kan vi tage $A$ og nul alle sub-diagonale elementer
- kan gøre det flere gange for hver kolonne på $a$
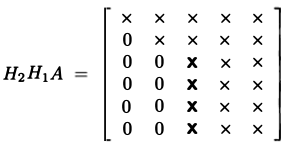
på denne måde kan vi udføre kr-nedbrydning:
Hessenberg nedbrydning
i stedet for at bruge det til at reducere matricen til trekantet, kan vi bruge Husholdertransformation til at reducere en matrice til Hessenberg Matrice