Termisk ledningsevne

termisk ledningsevne af faste stoffer er af forskellig art afhængigt af om de er ledere eller ej. I dielektrikum uden gratis elektriske ladninger overføres termisk energi af fononer. De kollektive vibrationer af atomer i krystalgitter har form af forskydningsbølger, hvis interferens genererer bølgepakker, dvs.fononer. Forskydningsbølgerne medfører udsving i densitet, der kan manifesteres som en variation af brydningsindeks. Hvis bølgerne passerer gennem et område, hvor brydningsindekset adskiller sig fra den gennemsnitlige volumetriske værdi, vil de efterfølgende forskydningsbølger, der bærer energien af termisk bevægelse, blive spredt.

spredningen er jo stærkere, jo mere er den maksimale afvigelse af atomer fra deres gennemsnitlige positioner i gitteret, dvs. jo højere T. Dette tegner sig for den eksperimentelt etablerede kendsgerning, at termisk ledningsevne af krystaldielektrikum falder ved forholdsvis høje temperaturer: liter1/T (Figur 1).

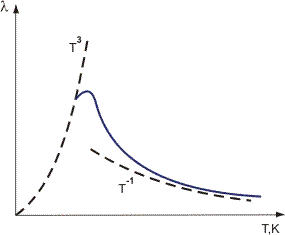
Figur 1. Variation af termisk ledningsevne af krystal dielektrikum med temperatur.

Debye gav et indblik i en peaklike karakter af Chr(t) variation ved lav T inden for rammerne af kvantemekaniske begreber. Han udarbejdede en dipolteori om dielektrikum baseret på begrebet et molekyle som en stiv dipol. I denne model introducerede Debye konceptet med den såkaldte Debye – temperatur, der er proportional med den maksimale frekvens af atomvibrationer i et fast stof. For de fleste stoffer er RISD enten lavere end eller tæt på rumtemperaturen (en undtagelse er diamant, for hvilken RISD = 1850 K og berrylium, for hvilken RISD = 1160k).

i kvanteteorien om faste stoffer betragtes krystalgitteret som et volumen fyldt med phonongas, hvortil fradraget af den enkleste kinetiske teori anvendes

hvor c er varmekapaciteten for et dielektrisk, der falder sammen med phonongas, V Den gennemsnitlige hastighed af fononer omtrent lig med lydhastigheden,den gennemsnitlige frie sti for fononer. Eksistensen af en bestemt endelig værdi på er resultatet af fononspredning på fononer, på defekter af krystalgitter og især på korngrænser over hele prøven. Temperaturafhængigheden(t) bestemmes af den påog c på temperaturen.

ved høje temperaturer, der væsentligt overstiger Debye-temperaturen, er den grundlæggende mekanisme, der begrænser, en phonon-phonon-spredning på grund af anharmonicitet af atomvibrationer i en krystal. Phonon-phonon – mekanismen for termisk modstand ((1/liter) er kendt som termisk modstandskoefficient) er kun mulig på grund af en overgang, der resulterer i retardering af fononstrømmen og mærkbar ændring af kvasi-momentum. Jo højere T, jo højere er sandsynligheden for overgangen medfaldende:(1/T). Siden ved t > stiger kølevarmekapaciteten c kun lidt med temperaturen, og derfor stiger den 1 / T.

ved temperaturer, der er lavere end Debye-temperaturen, T<<prisd, længden af den gennemsnitlige frie stibestemt af phonon-phonon-spredningen vokser drastisk,ekspristd/T og er som regel begrænset til størrelsen af en krystal R. ifølge Debye-loven varierer varmekapaciteten c i dette temperaturområde som c(T/prisd)3. Følgelig skal koefficienten for termisk ledningsevne ved t-kr 0 falde i forhold til T3. Den temperatur, for hvilken termisk ledningsevne har en top, bestemmes ud fra liter R, hvilket almindeligvis svarer til T-liter 0,05 liter.

denne teori tegner sig også for opførelsen af koefficienten for termisk ledningsevne for amorfe stoffer, der ikke har nogen lang rækkevidde, dvs.størrelsen af deres “krystaller” er af størrelsesordenen atomstørrelser. I kraft af dette skal spredning ved “grænserne” af disse stoffer overhovedet råde over t og krist const. Koefficienten for termisk ledningsevne af amorfe stoffer kur T3 ved lave temperaturer og skal vokse lidt, i forhold til varmekapacitet, ved moderate og høje temperaturer, T > kurpd.

alt dette giver en kvalitativ forklaring på afhængigheden af Krist(T) i ægte krystaldielektrikum, men tager ikke højde for afvigelser fra det konstante gitter på grund af atomurenheder af andre elementer og deres egne isotoper. Ved en høj temperatur er modstanden, der tilbydes af urenheder til varmetransport, uafhængig af temperaturen. Dette gør det muligt at estimere graden af krystalrenhed fra variation af dens termiske ledningsevne med temperatur. Den samme kendsgerning gør det muligt for os at bestemme fordelingen mellem glasagtig og krystalstof i det naturlige mineral, hvis glasset betragtes som en urenhed i en krystal.

termisk ledningsevne i metaller afhænger af bevægelse og interaktion mellem nuværende bærere, dvs.ledningselektroner. Generelt, måling af varmeledningsevne λ metal, der er lig med summen af gitter (gconf) λph, og elektron-λe komponenter, λ = λe + λph; ved almindelige temperaturer, som regel, λe >>λph.

hvis vi anvender en simpel kinetisk teori om gasser til strømmen af frie elektroner og antager, at længden af deres frie vej ikke afhænger af hastighed, så indebærer teorien det

hvor E er elektronladningen, K Boltsrnanns konstant, og KR. den elektriske ledningsevne. En streng kvantemekanisk teori tilbyder en lignende relation,

i begge formler ser forholdet mellem elektrondelen af koefficienten for termisk ledningsevne og elektrisk ledningsevne i et bredt temperaturområde ud til at være i forhold til temperaturen i henhold til loven om Vedemann-Frans, L/L = LT, hvor L er Lorentsen nummer. Denne lov bruges til at beregne kurer ud fra den målte elektriske ledningsevne. Imidlertid overtrædes det ved temperaturer under larsd, når en elektron-fonon−interaktion hersker (Larss vokser med faldende T som T−5, mens le varierer mere lidt som T-2).

de eksperimentelle fund viser, at termisk ledningsevne af metaller ved høje temperaturer som regel er en lidt faldende funktion af temperaturen. Men der er mange undtagelser. Således falder termisk ledningsevne af jern kraftigt med temperaturen, mens tantal og niob viser en positiv temperaturkoefficient.

af interesse er forsøgene på at sammenligne koefficienterne for termisk ledningsevne for forskellige stoffer for en enkelt karakteristisk temperatur, for eksempel for smeltepunktet Tm for faste stoffer. Således har den statistiske behandling af eksperimentelle data udført af Missenard vist, at termisk ledningsevne af metaller ved smeltepunktet larsi(T = Tm) = larsim er i forhold til larsiog termisk ledningsevne af dielektriske krystaller ved T = Tm er i forhold til, hvor m er molekylmassen, n antallet af atomer i den kemiske formel, er densiteten og smeltepunktet Tm i kelviner.

varmetransport i halvledere er mere kompleks end i dielektrikum og metaller, fordi fononet og elektronkomponenterne er lige så vigtige for dem. En anden grund til kompleksiteten er den betydelige virkning af urenheder, bipolar diffusion og andre lidt undersøgte faktorer på varmeoverførsel.

virkningen af tryk på termisk ledningsevne af faste stoffer kan antages, med en god nøjagtighed, at være lineær, liter for mange metaller, der vokser med p.

for effekten af porøsitet på termisk ledningsevne af faste stoffer se porøst Medium.