SSIM wurde erstmals im IEEE-Papier von 2004, Image Quality Assessment: From Error Visibility to Structural Similarity, vorgestellt. Die Zusammenfassung bietet eine gute Intuition in die Idee hinter dem vorgeschlagenen System,
Objektive Methoden zur Beurteilung der Wahrnehmungsbildqualität haben traditionell versucht, die Sichtbarkeit von Fehlern (Unterschieden) zwischen einem verzerrten Bild und einem Referenzbild unter Verwendung einer Vielzahl bekannter Eigenschaften des menschlichen visuellen Systems zu quantifizieren. Unter der Annahme, dass die menschliche visuelle Wahrnehmung in hohem Maße für die Extraktion von Strukturinformationen aus einer Szene geeignet ist, stellen wir einen alternativen ergänzenden Rahmen für die Qualitätsbewertung vor, der auf der Degradation von Strukturinformationen basiert.
Zusammenfassung: Die Autoren machen 2 wesentliche Punkte,
- Die meisten Bildqualitätsbewertungstechniken beruhen auf der Quantifizierung von Fehlern zwischen einem Referenz- und einem Beispielbild. Eine gängige Metrik besteht darin, die Differenz der Werte jedes der entsprechenden Pixel zwischen der Probe und den Referenzbildern zu quantifizieren (z. B. unter Verwendung des mittleren quadratischen Fehlers).
- Das menschliche visuelle Wahrnehmungssystem ist in hohem Maße in der Lage, strukturelle Informationen aus einer Szene zu identifizieren und somit die Unterschiede zwischen den aus einer Referenz- und einer Beispielszene extrahierten Informationen zu identifizieren. Daher wird eine Metrik, die dieses Verhalten repliziert, bei Aufgaben, bei denen zwischen einer Stichprobe und einem Referenzbild unterschieden werden muss, eine bessere Leistung erbringen.
Die Metrik Structural Similarity Index (SSIM) extrahiert 3 Schlüsselmerkmale aus einem Bild:
- Luminanz
- Kontrast
- Struktur
Der Vergleich zwischen den beiden Bildern wird auf der Grundlage dieser 3 Merkmale durchgeführt.
Figur 1 unten zeigt die Anordnung und den Ablauf des Strukturähnlichkeitsmesssystems. Signal X und Signal Y beziehen sich auf die Referenz- und Beispielbilder.

Aber was berechnet diese Metrik?
Dieses System berechnet den strukturellen Ähnlichkeitsindex zwischen 2 gegebenen Bildern, der ein Wert zwischen -1 und +1 ist. Ein Wert von +1 zeigt an, dass die 2 gegebenen Bilder sehr ähnlich oder gleich sind, während ein Wert von -1 anzeigt, dass die 2 gegebenen Bilder sehr unterschiedlich sind. Oft werden diese Werte so angepasst, dass sie in dem Bereich liegen, in dem die Extreme die gleiche Bedeutung haben.
Lassen Sie uns nun kurz untersuchen, wie diese Merkmale mathematisch dargestellt werden und wie sie zum endgültigen SSIM-Score beitragen.
- Luminanz: Die Luminanz wird durch Mittelung über alle Pixelwerte gemessen. Seine bezeichnet durch μ (Mu) und die formel ist unten angegeben,
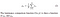
- Kontrast: Es wird gemessen, indem die Standardabweichung (Quadratwurzel der Varianz) aller Pixelwerte genommen wird. Es wird mit σ (sigma) bezeichnet und durch die folgende Formel dargestellt,
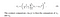
- Struktur: Der Strukturvergleich erfolgt unter Verwendung einer konsolidierten Formel (mehr dazu später), aber im Wesentlichen teilen wir das Eingangssignal mit seiner Standardabweichung, so dass das Ergebnis eine Standardabweichung aufweist, die einen robusteren Vergleich ermöglicht.
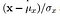
Jetzt haben wir die mathematische Intuition hinter den drei Parametern etabliert. Aber halt durch! Wir sind noch nicht fertig mit der Mathematik, ein bisschen mehr. Was uns jetzt fehlt, sind Vergleichsfunktionen, die die beiden gegebenen Bilder auf diesen Parametern vergleichen können, und schließlich eine Kombinationsfunktion, die sie alle kombiniert. Hier definieren wir die Vergleichsfunktionen und schließlich die Kombinationsfunktion, die den Ähnlichkeitsindexwert ergibt
- Luminanzvergleichsfunktion: Es wird durch eine Funktion definiert, l(x, y) welches unten gezeigt wird. μ (mu) repräsentiert den Mittelwert eines gegebenen Bildes. x und y sind die beiden Bilder, die verglichen werden.
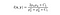
wobei C1 eine Konstante ist, um Stabilität zu gewährleisten, wenn der Nenner 0 wird. C1 ist gegeben durch,
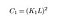
Update: Während des gesamten Artikels hatten wir nicht untersucht, was die K- und L-Konstanten in dieser Gleichung sind. Zum Glück hat ein Leser darauf in den Kommentaren hingewiesen, und um diesen Artikel ein bisschen hilfreicher zu machen, werde ich sie hier nur definieren.
L ist der Dynamikbereich für Pixelwerte (wir setzen ihn auf 255, da es sich um Standard-8-Bit-Bilder handelt). Sie können mehr darüber lesen, was die verschiedenen Bildtypen sind und was sie bedeuten, hier.
K1, K2 sind nur normale Konstanten, nicht viel da!
- Kontrastvergleichsfunktion: Sie wird durch eine Funktion c(x, y) definiert, die unten gezeigt wird. σ bezeichnet die Standardabweichung eines gegebenen Bildes. x und y sind die beiden Bilder, die verglichen werden.
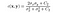
wobei C2 gegeben ist durch,
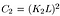
- Strukturvergleichsfunktion: Sie wird durch die unten gezeigte Funktion s (x, y) definiert. σ bezeichnet die Standardabweichung eines gegebenen Bildes. x und y sind die beiden Bilder, die verglichen werden.
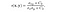
wobei σ(xy) definiert ist als,
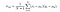
Und schließlich wird der SSIM-Score gegeben durch,

wobei α > 0, β > 0, γ > 0 die relative Wichtigkeit jeder der Metriken bezeichnen. Um den Ausdruck zu vereinfachen, können wir, wenn wir α = β = γ = 1 und C3 = C2 / 2 annehmen, Folgendes erhalten,
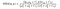
Aber es gibt einen Plot Twist!
Während Sie in der Lage wären, SSIM mit den obigen Formeln zu implementieren, ist es wahrscheinlich nicht so gut wie die gebrauchsfertigen Implementierungen, wie die Autoren erklären,
Für die Beurteilung der Bildqualität ist es sinnvoll, den SSIM-Index lokal und nicht global anzuwenden. Erstens sind bildstatistische Merkmale in der Regel stark räumlich nicht stationär. Zweitens können auch Bildverzerrungen, die von der lokalen Bildstatistik abhängen können oder nicht, raumvariant sein. Drittens kann bei typischen Betrachtungsabständen nur ein lokaler Bereich im Bild mit hoher Auflösung durch den menschlichen Beobachter in einem zeitlichen Fall wahrgenommen werden (wegen der Foveationsfunktion des HVS). Und schließlich kann eine lokalisierte Qualitätsmessung eine räumlich variierende Qualitätskarte des Bildes liefern, die mehr Informationen über die Qualitätsverschlechterung des Bildes liefert und in einigen Anwendungen nützlich sein kann.
Zusammenfassung: Anstatt die obigen Metriken global anzuwenden (dh im gesamten Bild gleichzeitig), ist es besser, die Metriken regional anzuwenden (dh in kleinen Abschnitten des Bildes und unter Berücksichtigung des Mittelwerts insgesamt).
Diese Methode wird oft als mittlerer struktureller Ähnlichkeitsindex bezeichnet.
Aufgrund dieser Änderung des Ansatzes verdienen unsere Formeln auch Änderungen, um dasselbe widerzuspiegeln (es sollte beachtet werden, dass dieser Ansatz üblicher ist und zur Erläuterung des Codes verwendet wird).
(Hinweis: Wenn der Inhalt unten etwas überwältigend erscheint, keine Sorge! Wenn Sie das Wesentliche verstehen, erhalten Sie durch den Code eine viel klarere Vorstellung.)
Die Autoren verwenden eine 11×11 kreissymmetrische Gaußsche Wägefunktion (im Grunde eine 11×11-Matrix, deren Werte aus einer gaußschen Verteilung abgeleitet sind), die sich Pixel für Pixel über das gesamte Bild bewegt. Bei jedem Schritt werden die lokalen Statistiken und der SSIM-Index im lokalen Fenster berechnet. Da wir die Metriken jetzt lokal berechnen, werden unsere Formeln wie folgt überarbeitet,
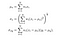
Wobei wi die gaußsche Gewichtungsfunktion ist.
Wenn Sie das etwas unintuitiv fanden, keine Sorge! Es genügt, sich wi als Multiplikanden vorzustellen, der verwendet wird, um die erforderlichen Werte mit Hilfe einiger mathematischer Tricks zu berechnen.
Sobald Berechnungen im gesamten Bild durchgeführt wurden, nehmen wir einfach den Mittelwert aller lokalen SSIM-Werte und gelangen zum globalen SSIM-Wert.
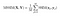
Endlich fertig mit der Theorie! Nun zum Code!