EINFÜHRUNG
Konkurrierende Risiken (CR) werden seit dem 18. Gelegentlich wurden Arbeiten im statistischen oder mathematischen Bereich veröffentlicht, die neue Entwicklungen einbeziehen, einschließlich der Monographie von David und Moeschberger.1 Als die Daten in Bezug auf die verschiedenen Arten von Ergebnissen umfangreicher, klarer und präziser wurden, tauchte CR als entscheidende Art der Analyse innerhalb der Time-to-Event-Analyse wieder auf, die für ein besseres Verständnis einer Krankheit erforderlich ist. Die Verbindung zwischen den mathematischen Ergebnissen und dem angewandten Feld musste hergestellt werden. Mehrere Autoren haben zum Verständnis von CR-Situationen beigetragen.2, 3 Andere Autoren verbesserten und entwickelten Techniken und stellten in einigen Fällen gebrauchsfertigen Computercode für angewandte Statistiken zur Verfügung.4, 5, 6
EINFÜHRUNG IN DIE TIME-TO-EVENT-ANALYSE
In vielen Studien wird das Ergebnis longitudinal beobachtet. Auf diese Weise wird jedes Subjekt in der Kohorte für einen Zeitraum beobachtet, bis das Ereignis eintritt. Zum Beispiel kann das Ereignis von Interesse Tod, Herzinfarkt oder Wiederauftreten von Krebs sein. Die Ziele der Studie können darin bestehen, die Wahrscheinlichkeit des Auftretens des Ereignisses oder seine Assoziation mit Kovariaten von Interesse wie Behandlung oder Subjektmerkmale. Die verwendete statistische Analyse wird als Time-to-Event-Analyse oder manchmal als Überlebensanalyse bezeichnet. Die gebräuchlichste Methode zur Schätzung der Wahrscheinlichkeit eines Ereignisses ist ein nichtparametrischer Ansatz, der üblicherweise als Kaplan-Meier7 (KM) – oder Produktlimitmethode bezeichnet wird. Die Hauptannahme der KM-Schätzung für das Überleben ist, dass die zensierten Beobachtungen das Ereignis erleben werden, wenn sie lange genug verfolgt werden.
Für den Rest dieses Artikels werden die Wahrscheinlichkeiten für das Ereignis und nicht die Wahrscheinlichkeit für ereignisfrei angegeben. Beispielsweise wird anstelle der Überlebenswahrscheinlichkeit die Todeswahrscheinlichkeit dargestellt, die mit dem Komplement des KM-Schätzers geschätzt werden kann: 1-KM.
EINFÜHRUNG IN KONKURRIERENDE RISIKEN
Es ist nicht ungewöhnlich, dass ein Studienteilnehmer mehr als eine Art von Ereignis erlebt. Eine ähnliche Situation tritt auf, wenn das Auftreten eines Ereignistyps die Fähigkeit ändert, das interessierende Ereignis zu beobachten. Miyasaka et al.8 führte eine Studie an einer gemeinschaftsbasierten Kohorte von Patienten durch, bei denen zwischen 1986 und 2000 in Olmsted County, Minnesota, USA, Vorhofflimmern diagnostiziert wurde. Das primäre Ergebnis war der Beginn der Demenz. Das mediane Follow-up betrug 4,6 Jahre. Andere Arten von Ereignissen waren Schlaganfall und Tod. Von den 2837 Personen mit Vorhofflimmern hatten 299 Demenz und 1638 starben zum Zeitpunkt der Analyse. Die Zahlen mit Schlaganfall werden nicht gemeldet und in der Analyse zensiert. Die Schlussfolgerung der Studie war, dass die Inzidenz von Demenz bei den Personen mit Vorhofflimmern häufig ist (10,5% nach 5 Jahren mit KM-Methode). Das Auftreten eines Schlaganfalls vor Demenz hat keinen Einfluss auf die Beobachtung von Demenz und ist daher kein seltenes Ereignis. Aus Gründen der Argumentation ignorieren wir die Tatsache, dass mehrere Schlaganfälle Demenz verursachen können. Andererseits macht ein Tod ohne vorherige Demenz die Beobachtung von Demenz unmöglich. Daher ist ein Tod ohne Demenz ein Schlüsselereignis für den Endpunkt der Demenz. Auch eine schwere Kopfverletzung kann als CR-Ereignis angesehen werden, da die Verhaltensänderungen des Patienten die Diagnose einer Demenz unmöglich machen können.
Eine subtilere CR-Situation tritt in der Studie von Whalley et al.9 der Bedeutung der Echokardiographie. Diese Kohorte von 228 älteren symptomatischen Patienten unterzog sich einer Echokardiographie und wurde entweder für einen kardiovaskulären Krankenhausaufenthalt oder für einen kardiovaskulären Tod beobachtet. Die Hypothese war, dass die Echokardiographie Merkmale für kardiovaskuläres Ereignis vorhersagen. Das Hauptergebnis war definiert als die zusammengesetzte Maßnahme einschließlich kardiovaskulärer Tod und / oder Krankenhausaufenthalt. Für diese Art von Ergebnis ist ein Tod aufgrund anderer Ursachen als Herz-Kreislauf-Erkrankungen ein CR-Ereignis, und als solches besteht für einen Patienten kein Risiko mehr, eines der Ereignisse von Interesse zu haben.
Eine 3-armige, doppelblinde, randomisierte Studie wurde in 931 Zentren und 24 Ländern durchgeführt, um die Wirkung von Valsartan vs. Valsartan + Captopril vs. Captopril allein (VALIANT)10 auf die Gesamtmortalität zu testen. Insgesamt traten 14 703 Patienten nach Myokardinfarkt mit linksventrikulärer Dysfunktion und / oder Herzinsuffizienz 1:1: 1 in den 3 Armen auf. Da jeder Tod als Ereignis angesehen wurde, hat diese Art von Ergebnis keine Konsequenzen. Die Studie stützte die Hypothese, dass das Überleben in den 3 Armen unterschiedlich war. Gastrointestinale (GI) Blutungen wurden jedoch in allen 3 Armen als schwerwiegende Nebenwirkung identifiziert. In: Moukarbel et al.11 untersuchten die möglichen Faktoren, die GI-Blutungen vorhersagen könnten. Für diesen Endpunkt ist der Tod ohne GI-Blutung ein klares Zeichen.
Immer mehr Forscher erkennen das Vorhandensein von CR und die Notwendigkeit, geeignete Techniken anzuwenden. Eine Kohorte von 972 Patienten mit akutem Koronarsyndrom ohne ST-Segment-Elevation zwischen 2001 und 2005 wurde von Núñez et al.12 Eines der Ziele der Studie war es, Faktoren zu finden, die mit einer Rehospitalisierung bei akuter Herzinsuffizienz zusammenhängen. Zu den untersuchten Faktoren gehörten Diabetes, Vorgeschichte einer ischämischen Herzerkrankung, chronisches Nierenversagen, Rauchgeschichte und Behandlungsgeschichte. Die Autoren erkannten die Möglichkeit von CR wie Tod vor der Rehospitalisierung und wendeten spezifische Techniken korrekt an, um die CR-Situation zu berücksichtigen.
Melberg et al.13 untersuchte eine Kohorte von 1234 Patienten mit symptomatischer koronarer Herzkrankheit, die 2 Arten von Behandlungen erhielten: koronararterien-Bypass-Transplantation (n = 594) oder perkutane Koronarintervention (n = 640). Von den 301 Todesfällen, die während der Nachuntersuchung beobachtet wurden, waren 42, 5% kardiale Todesfälle und der Rest nicht kardiale Todesfälle. Die Autoren präsentieren Ergebnisse für die Gesamtmortalität sowie für die kardiale Mortalität und die nicht-kardiale Mortalität. Sie weisen darauf hin, dass der Prozentsatz der Gesamtmortalität die Summe des Prozentsatzes der kardialen und nicht kardialen Mortalität ist, der unter Berücksichtigung der CR korrekt geschätzt wird. Die Autoren betonen, wie wichtig es ist, jedes der Ereignisse von Interesse zu analysieren, anstatt sie zu einem Gesamtbild zu kombinieren. Dieses Thema wird auch auf einer allgemeineren Ebene von Mell und Jeong erläutert.14
Wie aus den obigen Beispielen vermutet werden könnte, ist die Hauptfrage, wenn CR vorhanden sind, ob die CR ignoriert und die Beobachtungen mit CR zensiert oder CR berücksichtigt werden soll. Wenn die CR ignoriert und die CR-Beobachtungen zensiert werden, reduziert sich die Analyse auf ein „übliches“ Time-to-Event-Szenario. Aufgrund der Vertrautheit dieser Art von Analyse und der Verfügbarkeit von Software greifen viele Forscher auf diesen Ansatz zurück, wie in den früheren Beispielen gezeigt. Es ist jedoch nicht nur unter Statistikern einstimmig2, 15, 16, 17, 18 dass die Schätzung der Ereigniswahrscheinlichkeit in diesem Fall die wahre Wahrscheinlichkeit überschätzt. Die nächste natürliche Frage ist, ob die Modellierung innerhalb dieser Grenzen durchgeführt werden kann (Ignorieren / Zensieren von CR). Dies ist mehrdeutiger und schwieriger zu verstehen. Während eine solche Analyse nicht ohne Wert sein kann, ist ihre Interpretation fast immer mit Schwierigkeiten verbunden. Die Hauptanforderung ist, dass das CR-Ereignis (dessen Beobachtungen zensiert und mit den echten zensierten Beobachtungen gemischt wurden) unabhängig vom interessierenden Ereignis sein muss. Wenn dies der Fall ist, könnten die Ergebnisse als Effekt von Kovariaten interpretiert werden, wenn die CR-Ereignisse nicht existierten. Diese Annahme kann jedoch normalerweise nicht gemacht und nicht verifiziert oder getestet werden. Zusammenfassend lässt sich sagen, dass jedes Mal, wenn die CR-Beobachtungen zensiert werden, die Schätzung der Ereigniswahrscheinlichkeit falsch ist und die Interpretation der Wirkung von Kovariaten aufgrund der fehlenden Kenntnis der Unabhängigkeit zwischen dem interessierenden Ereignis und dem CR-Ereignis nicht klar ist.
Wenn die Analyse unter Berücksichtigung von CR durchgeführt wird (und sich deutlich vom interessierenden Ereignis oder der Zensur unterscheidet), wird die Wahrscheinlichkeit korrekt geschätzt und die Modellierung hat eine einfache Interpretation. Es gibt keine Annahme der Unabhängigkeit, um die Interpretation zu behindern. Der so geschätzte Koeffizient einer Kovariate repräsentiert den Effekt dieser Kovariate auf die beobachteten Wahrscheinlichkeiten.
Mehrere Autoren19, 20 versuchten, die beiden Ansätze in Bezug auf die Leistungsfähigkeit der Tests mithilfe von Simulationen zu vergleichen. Der Forscher muss sich jedoch bewusst sein, dass das Hauptproblem in der Interpretation der Ergebnisse liegt. Unabhängig davon, wie leistungsfähig die Tests sind, muss die Analyse die Frage der Studie beantworten.
SCHÄTZEN DER WAHRSCHEINLICHKEIT EINES EREIGNISSES
Es ist üblich, die KM-Methode anzuwenden, um die Wahrscheinlichkeit eines Ereignisses abzuschätzen. Die typische Formel für die KM-Schätzung lautet
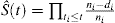
, wobei t1t2t3ni die Anzahl der Risikopatienten zum Zeitpunkt ti und di die Anzahl der Ereignisse zum Zeitpunkt ti darstellt.
Diese Formel kann durch algebraische Manipulation transformiert werden, um die Wahrscheinlichkeit eines Ereignisses als:
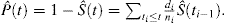
In Gegenwart von CR gibt es mindestens 2 Arten von Ereignissen: Ereignis von Interesse, identifiziert mit dem Index e, und das konkurrierende Risikoereignis, identifiziert mit dem Index c. Kalbfleisch und Prentice führten die Formel für die Wahrscheinlichkeit eines interessanten Ereignisses in Gegenwart von CR ein:
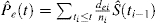
Es ist interessant, die Beziehung zwischen (1) und (2) zu beachten. Da di die Anzahl aller Ereignisse bei ti ist, kann es als die Summe der Anzahl der Ereignisse von Interesse dei und der Anzahl der CR-Ereignisse dci zum Zeitpunkt ti konzipiert werden. Als solches kann die Wahrscheinlichkeit jeder Art von Ereignis zerlegt werden als:
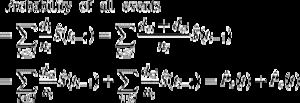
Somit kann die Wahrscheinlichkeit aller Ereignisse in die Wahrscheinlichkeiten für jede Art von Ereignis zerlegt werden.
Wenn 1-KM verwendet wird, um die Wahrscheinlichkeit eines Ereignisses von Interesse in Gegenwart von CR zu berechnen, wird das Überleben aller Ereignisse in Formel (2) durch die KM-Schätzung ersetzt, die nur auf den Ereignissen von Interesse basiert. Dies wird die Ergebnisse verzerren, wie später gezeigt wird. Die Hauptannahme für die Verwendung der KM-Methode ist, dass die zensierten Patienten, wenn sie lange genug verfolgt werden, das Ereignis schließlich erleben werden. Wenn jedoch die KM-Methode in Gegenwart von CR angewendet wird, werden die Patienten, bei denen andere Arten von Ereignissen als das interessierende Ereignis auftreten, normalerweise zensiert, obwohl sie für das interessierende Ereignis nicht mehr gefährdet sind. Darüber hinaus kann die Nice-Zerlegung in (3) nicht für die 1-KM-Formel durchgeführt werden.
In angewandten Situationen ist es möglich, dass es mehrere andere Arten von Ereignissen gibt, die nicht von Interesse sind. In diesem Fall können alle unter dem Dach von CR-Ereignissen zusammengefasst werden.
Anhand eines Beispiels wird gezeigt, dass die Verwendung der KM-Methode in Gegenwart von CR nicht geeignet ist.
Beschreibung des Beispiels
Zur Veranschaulichung wird ein Datensatz verwendet, der zur Untersuchung der Spätwirkungen der Behandlung des Hodgkin-Lymphoms gesammelt wurde. Das Hauptergebnis ist ein Krankenhausaufenthalt wegen Herzerkrankungen. Das Hodgkin-Lymphom ist eine Krebsart, die vor allem bei jungen Erwachsenen auftritt. In seinen frühen Stadien ist es fast heilbar, mit 10-Jahres-Gesamtüberleben von 70%. Daher ist eine Kohorte dieser Patienten ideal, um die langfristigen Nebenwirkungen der Behandlung zu untersuchen. Der hier verwendete Datensatz ist eine Teilmenge einer größeren Kohorte, die an anderer Stelle gemeldet wird. Die Daten werden auch geändert, um unseren Zwecken zu dienen. Der Einfachheit halber haben wir beispielsweise nur Patienten mit Chemotherapie oder Bestrahlung in den Daten gespeichert, ausgenommen Patienten mit kombinierter Behandlung. Um die CR-Rate (Tod ohne kardialen Krankenhausaufenthalt) zu erhöhen, schlossen wir Patienten aller Stadien ein. Einige Follow-up- und Todesdaten wurden unterstellt. Aufgrund der Änderungen, die an den Daten vorgenommen wurden, können aus dieser Analyse keine klinischen Schlussfolgerungen gezogen werden. Die hier vorgestellten Daten beziehen sich auf 689 Datensätze mit 93 kardialen Krankenhausaufenthalten und 467 Todesfällen.
Die Raten für kardiale Krankenhausaufenthalte und für Tod ohne kardiales Ereignis wird sowohl mit der KM-Methode (1) als auch mit der kumulativen Inzidenzfunktion (CIF) eingeführt von Kalbfleisch und Prentice21 für diesen Zweck (2).
Die Kaplan-Meier-Methode, die auf eine konkurrierende Risikosituation angewendet wurde, überschätzt die wahre Rate des Ereignisses
Abbildung 1 zeigt die CIF- und 1-KM-Schätzungen für die kardiale Hospitalisierung der Gruppe, die nur mit Chemotherapie behandelt wurde. Die gestrichelte Linie, die den 1-KM-Schätzungen entspricht, liegt über der durchgezogenen Linie, die die CIF-Schätzungen darstellt. Es kann mathematisch gezeigt werden, dass 1-KM die Wahrscheinlichkeit eines Ereignisses immer überschätzt. Ein häufiges Missverständnis ist, dass 1-KM-Schätzungen korrekt sind, wenn die beiden Ereignisse unabhängig voneinander sind. Die Unabhängigkeit zwischen Ereignissen ist bestenfalls immer fraglich, aber selbst wenn die Daten als unabhängige Ereignisse simuliert werden, besteht der Unterschied zwischen den CIF-Schätzungen und den 1 KM. Die Größe der Differenz hängt von der Anzahl der Ereignisse ab, sowohl für Ereignisse von Interesse als auch für die CR-Ereignisse. In Miyasaka et al.,8 die Inzidenz von Demenz nach 5 Jahren mit der KM-Methode betrug 10,5%. Die Anzahl der CR (Todesfälle) betrug etwa drei Viertel der Gesamtzahl der Ereignisse, was darauf hindeutet, dass ihre Schätzung viel größer sein könnte als das, was beobachtet wird.
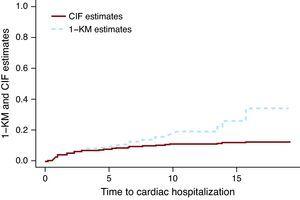
Abbildung 1. Kumulative Inzidenzfunktion vs 1- Kaplan-Meier-Schätzungen.. CIF, kumulative Inzidenzfunktion; KM, Kaplan-Meier.
Die kumulative Inzidenzfunktion partitioniert die Wahrscheinlichkeit eines Ereignisses (kardialer Krankenhausaufenthalt oder Tod) in die konstituierenden Wahrscheinlichkeiten
Algebraisch wird dies in (3) bewiesen. Für ein tieferes Verständnis der Funktionsweise wird jedoch grafisch gezeigt, dass von der Wahrscheinlichkeit aller Ereignisse ein Teil an der CIF für ein Ereignis und der andere an der CIF für das andere Ereignis teilnimmt. Abbildung 2A zeigt die Wahrscheinlichkeit eines Ereignisses: Herz-Krankenhausaufenthalt oder Tod ohne Herz-Krankenhausaufenthalt. Abbildung 2B enthält nur die Kurve zwischen 10.7 und 10.85 Jahre, so dass die Schritte sichtbar sind. Auf jedem Schritt befindet sich ein Kreis. Die offenen Kreise erscheinen auf den Stufen, in denen ein Tod beobachtet wurde, während die durchgezogenen Kreise auf den Stufen sind, in denen ein Herzkrankenaufenthalt stattgefunden hat. Die Schritte mit durchgezogenen Kreisen nehmen an der CIF für den Herz-Krankenhausaufenthalt in Panel C teil und diejenigen mit offenen Kreisen nehmen an der Kurve für den Tod in teil Abbildung 2D. Somit trägt jeder Schritt zur Wahrscheinlichkeit des Ereignisses bei, das ihn verursacht. Auf diese Weise ist die Wahrscheinlichkeit aller Ereignisse zu jedem Zeitpunkt die Summe der Wahrscheinlichkeit des interessierenden Ereignisses und der Wahrscheinlichkeit von CR. Beachten Sie, dass die letzten 3 Felder (Abbildung 2B-D) das gleiche Zeitfenster zeigen und die gleiche Länge für die y-Achse haben, sodass die Größe der Schritte zwischen ihnen verglichen werden kann. Tabelle 1 zeigt diese Wahrscheinlichkeiten nach 1, 2, 3, 4 und 5 Jahren.
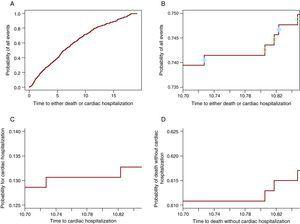
Abbildung 2. Die Aufteilung der Wahrscheinlichkeit aller Ereignisse in die konstituierenden Wahrscheinlichkeiten. A. Die Wahrscheinlichkeit eines Herzkrankenhauses oder Todes. B. Die Wahrscheinlichkeit eines kardialen Krankenhausaufenthaltes oder Todes nur für das Zeitfenster 10,70 – 10,85 Jahre. Die durchgezogenen Kreise zeigen den Herzstillstand an und die offenen Kreise stellen Todesfälle ohne Herzstillstand dar. C. Die Wahrscheinlichkeit einer kardialen Hospitalisierung im Zeitfenster 10,70 -10,85 Jahre. D. Die Wahrscheinlichkeit des Todes ohne Herz Hospitalisierung im Zeitfenster 10,70-10,85.
Tabelle 1. Die Wahrscheinlichkeit für jedes Ereignis ist die Summe der konstituierenden Wahrscheinlichkeiten.
| Berichtsjahr | Wahrscheinlichkeit eines Herzstillstands | Todeswahrscheinlichkeit | Wahrscheinlichkeit eines Herzstillstands oder Todes |
| 1 | 0.038 | 0.054 | 0.092 |
| 2 | 0.054 | 0.139 | 0.193 |
| 3 | 0.072 | 0.193 | 0.265 |
| 4 | 0.076 | 0.25 | 0.327 |
| 5 | 0.087 | 0.305 | 0.392 |
Da der 1-KM die Wahrscheinlichkeit für ein Ereignis überschätzt, würden wir, wenn wir versuchen würden, die 1-KM-Schätzungen für einen Herzstillstand zu den 1-KM für den Tod hinzuzufügen, eine viel höhere Rate erhalten als die Wahrscheinlichkeit eines Ereignisses. In einigen Fällen ist die erhaltene Zahl sogar größer als 1, was beweist, dass 1-KM-Schätzungen in Gegenwart von CR nicht einmal Wahrscheinlichkeiten sind.
Schätzt die kumulative Inzidenzfunktionsmethode tatsächlich die korrekte Ereigniswahrscheinlichkeit?
Zu diesem Zweck wurde ein Datensatz von 500 Datensätzen simuliert, so dass es vor 5 Jahren keine Zensur gibt und es 2 Arten von Ereignissen gibt: Typ 1und 2. Tabelle 2 zeigt für jede Art von Ereignis die bis zu diesem Zeitpunkt beobachtete Anzahl, die Rohrate und die CIF-Schätzung, die genau gleich sind. Dies geschieht nur, wenn bis zu diesem Zeitpunkt keine zensierten Beobachtungen vorliegen. Bei zensierten Beobachtungen innerhalb der gemeldeten Jahre gilt die Gleichheit nicht, und der richtige Weg zur Schätzung der Wahrscheinlichkeit ist der CIF und nicht der Rohkurs.
Tabelle 2. Die Wahrscheinlichkeit der beiden Arten von Ereignissen, wenn keine zensierten Beobachtungen vorliegen, beträgt bis zu 5 Jahre.
CIF, kumulative Inzidenzfunktion.
Um die Wahrscheinlichkeit eines Ereignisses in Gegenwart von CR zu berechnen, muss abschließend die von Kalbfleisch und Prentice eingeführte Methode verwendet werden, die üblicherweise als kumulative Inzidenzkurve bezeichnet wird.
MODELLIERUNG
Ein wichtiger Aspekt in einer Analyse ist es, die Assoziation zwischen einer Kovariate und dem interessierenden Ereignis zu testen, entweder allein oder unter Berücksichtigung anderer Faktoren. In Abwesenheit von CR wird dies routinemäßig unter Verwendung des Cox Proportional Hazards (Cox PH) -Modells erreicht.22
In Gegenwart von CR hat das Cox-PH-Modell keine einfache Interpretation. Wenn die Zeit bis zu den 2 Ereignistypen als unabhängig betrachtet werden kann, können die Ergebnisse so interpretiert werden, dass sie den Effekt in der Situation zeigen, in der sie nicht existieren. Die Annahme der Unabhängigkeit kann jedoch selten getroffen oder getestet werden, und daher sind die Ergebnisse des Cox-PH-Modells in der Regel nicht interpretierbar.
Feines und graues Modell
Feines und graues Modell (F & G) modifizierte das Cox-PH-Modell, um das Vorhandensein von CR zu ermöglichen. Die technische Modifikation besteht darin, die CR-Beobachtungen mit abnehmendem Gewicht im Risikoset zu halten. Auf diese Weise modelliert die F& G-Methode die Subdistributionsgefahren. Der mit dem F & G-Modell geschätzte Effekt zeigt die aktuellen und realen Unterschiede zwischen den Behandlungsgruppen in Bezug auf die Unterverteilungsrisikoverhältnisse. Die Annahme der Proportionalität der Gefahren ist immer noch eine Anforderung, bezieht sich aber natürlich auf die Unterverteilungsgefahren. Das F & G-Modell kann zeitabhängige Koeffizienten aufnehmen, um die Nichtproportionalität von Gefahren zu modellieren. Dieses Modell kann sowohl auf das Ereignis von Interesse (kardialer Krankenhausaufenthalt) als auch auf das CR (Tod) angewendet werden.
Die Modelle Cox PH und F& G wurden auf den Hodgkin-Lymphom-Datensatz angewendet, um die Behandlungsoption Chemotherapie vs. Bestrahlung zu testen. Für dieses Beispiel (Tabelle 3) unterscheiden sich die Ergebnisse der Modelle Cox PH und F&G erheblich (erste 2 Zeilen). Wie oben erwähnt, sind die Cox-PH-Ergebnisse nicht interpretierbar und können nicht verwendet werden. Die zweite Reihe zeigt, dass es in der Strahlengruppe mehr Herzkrankenhäuser gibt, und die dritte Reihe zeigt mehr Todesfälle in der Chemotherapiegruppe. Abbildung 3 zeigt diese Ergebnisse grafisch. Es ist möglich, dass Patienten mit fortgeschrittener Erkrankung eine Chemotherapie allein erhielten, und diese Patienten starben auch häufiger an ihrem Krebs. Auf der anderen Seite wurde Strahlung allein wahrscheinlich Patienten in einem frühen Stadium gegeben, die länger nach der Hodgkin-Lymphom-Diagnose lebten. Diese Patienten hatten eher eine Chance, späte Nebenwirkungen wie Herzerkrankungen zu entwickeln.
Tabelle 3. Die Wirkung der Behandlung, wenn Cox Proportional Gefahren und Fein- und Grau-Modelle eingesetzt werden.
CI, Konfidenzintervall; Cox PH, Cox proportional Hazards Modell; F&G, Fein- und Graumodell; HR, Hazard Ratio.
Die Hazard Ratios zeigen die Zunahme der Gefahren für die Strahlengruppe im Vergleich zur Chemotherapiegruppe.
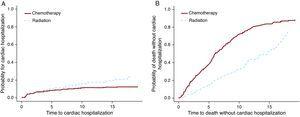
Abbildung 3. Die Wirkung der Behandlung für Herz-Krankenhausaufenthalt und für den Tod.
Wie aus diesem Beispiel hervorgeht, ist die Interpretation der Ergebnisse eine Zusammenarbeit zwischen dem Statistiker und dem Kliniker, der über gründliche Kenntnisse der Krankheit verfügt.
Das Vorhandensein von CR erschwert sowohl die Analyse als auch die Interpretation von Daten. Damit der Leser die Ergebnisse richtig interpretieren kann, müssen die Autoren Details zu den beobachteten Ereignissen angeben, auch wenn sie auf den ersten Blick nicht wichtig erscheinen. Wenn der Endpunkt im Laufe der Zeit beobachtet wird, müssen die Autoren daher das interessierende Ereignis einbeziehen, ob die Möglichkeit einer CR besteht, wie viele Patienten eine dieser Arten von Ereignissen erleben und die Dauer der Nachsorge. In Gegenwart von CR ist es informativ, die Analyse für das interessierende Ereignis sowie die Analyse für CR einzubeziehen, da sie sich ergänzen und zur Interpretation der Ergebnisse beitragen können.
Der logistische Ansatz
Nehmen wir zunächst an, dass wir uns im Rahmen von no CR befinden. Wenn das Ergebnis innerhalb eines kurzen Intervalls (z. B. 1 Jahr) erwartet wird, ist das Werkzeug der Wahl für viele Forscher die logistische Regression. Dies ist angemessen, wenn jede Person in der Kohorte die minimale Nachbeobachtungszeit hat, in diesem Fall 1 Jahr. Tatsächlich stimmt die Schätzung für die 1-Jahres-Mortalität mit der Schätzung von 1 KM überein. Der zeitliche Grenzwert muss für jedes Individuum in der Kohorte gleich sein. Wenn das interessierende Ergebnis die 1-Jahres-Mortalität ist und 1 Person in der Kohorte nach 1 Jahr und 2 Tagen stirbt, sollte diese Person daher als „kein Ereignis nach 1 Jahr“ betrachtet werden.“ Dies kann die Anzahl der Ereignisse reduzieren, was zu einer weniger als idealen Analyse führt, wenn viele beobachtete Ereignisse nach dem Grenzwert auftreten.
Die gleichen Grundregeln gelten, wenn CR vorhanden sind. Für alle Personen in der Kohorte muss der Mindestnachverfolgungspunkt als Zeitgrenzwert gewählt werden, und dieser Grenzwert muss für alle Personen in der Kohorte gelten. Die Koeffizienten und p-Werte geben im Allgemeinen die gleiche Nachricht, sind jedoch für die logistische Regression im Vergleich zum F & G-Modell nicht genau gleich. Zunächst stellt der Koeffizient in der logistischen Regression das Protokoll der Odds Ratio dar, während er im F& G-Modell das Protokoll des Verhältnisses der beiden Unterverteilungen ist. Darüber hinaus werden in der logistischen Analyse nicht alle Ereignisse verwendet und natürlich wird ein anderes Modell verwendet.
LEISTUNGSBERECHNUNG
Wenn das Maß Time-to-Event ist, hat die Leistungsberechnung zwei Stufen. Der erste Schritt besteht darin, die Anzahl der Ereignisse zu berechnen, die erforderlich sind, um eine bestimmte Effektgröße zu erkennen. Als nächstes wird die Anzahl der Patienten berechnet, die benötigt werden, um diese Anzahl von Ereignissen zu beobachten. In den vorherigen Abschnitten wurde betont, dass es bei Vorhandensein von CR nicht möglich ist, alle interessanten Ereignisse aufgrund des Auftretens von CR zu beobachten. Da die Anzahl der Ereignisse bei der Berechnung der Leistung von zentraler Bedeutung ist, muss besonders darauf geachtet werden, dass sie berücksichtigt werden. Wenn die Ergebnisse nicht berücksichtigt werden, ist die Studie zu schwach und daher wahrscheinlich erfolglos (und möglicherweise unethisch).
SOFTWARE
Die Open Source R Software auf CRAN (the Comprehensive R Archive Network) Seite (http://cran.r-project.org/) bietet ein Paket (cmprsk) implementiert von Dr. Robert Gray enthält die notwendigen Werkzeuge für eine vollständige Analyse Buchhaltung für CR. Somit könnte man beobachtete Wahrscheinlichkeitsdiagramme für das interessierende Ereignis und einen p-Wert basierend auf dem Gray-Test erhalten, der ein modifizierter Logrank-Test für die CR-Situation ist. Innerhalb des Pakets gibt es auch eine Funktion zur Modellierung mit dem F& G-Ansatz. Luca Scruca verbesserte die Ausgabe der Modellierungsfunktion für ein einfacheres Lesen, indem er eine zusammenfassende Funktion in das Paket integrierte. Das Modell hat die Möglichkeit, die Proportionalität von Gefahren zu überprüfen, und Terme für zeitabhängige Koeffizienten können einbezogen werden. Der Code kann keine linken Trunkierungs- oder Clusterdaten aufnehmen. Die linke Kürzung wäre nützlich für die Analyse mehrerer / wiederkehrender Ereignisse pro Patient oder für die Analyse der Fallkohorte. Ein Code für Fallkohortenstudien wurde entwickelt (Pintilie et al.23) und kann von den Autoren bezogen werden. Zhou et al.24 erweiterte das F & G-Modell um geschichtete Daten und wird auch eine Version für Clusterdaten haben. Zu diesem Zeitpunkt kann der Code für beide Fälle von den Autoren bezogen werden, es ist jedoch wahrscheinlich, dass er an CRAN gesendet wird.
STATA 11 hat kürzlich das F&G-Modell implementiert. Man muss sich bewusst sein, dass die mit STATA erhaltenen Graphen eher prädiktive als beobachtete Wahrscheinlichkeitsgraphen sind. Es gibt zwei Einschränkungen, wenn vorhergesagte Kurven verwendet werden: a) Die Linien erscheinen immer so, als ob die Proportionalität der Gefahren erfüllt wäre, und b) Die Anzahl der Schritte in jeder Kurve ist größer als die Anzahl der Ereignisse in jeder Untergruppe, was den Eindruck erweckt, dass es mehr Ereignisse gibt, als es wirklich gibt.
SCHLUSSFOLGERUNGEN
Die Verfügbarkeit großer Datensätze mit vollständigem Follow-up für mehrere Endpunkte nimmt kontinuierlich zu. Es besteht auch ein zunehmender Bedarf an Analysen, die sich mit einem genauen Endpunkt wie dem Tod durch Herzinsuffizienz oder der Krankheitskontrolle oder der Kontrolle lokaler Krankheiten befassen. Alle diese Endpunkte könnten möglicherweise CR haben. Daher ist es wichtig, dass die CR von der Entwurfsphase bis zur Interpretation der Ergebnisse berücksichtigt wird. Während das Cox-PH-Modell einen begrenzten Wert haben kann, wenn die Unabhängigkeit berücksichtigt wird, sind die KM-Schätzungen nicht korrekt und können nicht interpretiert werden. Daher müssen spezifische Techniken wie CIF- und F & G-Modelle, die in R und teilweise in STATA verfügbar sind, angewendet werden.
INTERESSENKONFLIKTE
Keine deklariert.