Das elektrische Feld E kann immer als Gradient einer skalaren Potentialfunktion ausgedrückt werden
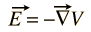
Es gibt kein allgemeines skalares Potential für das Magnetfeld B, aber es kann als Ergebnis einer Vektorfunktion ausgedrückt werden
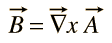
Diese Funktion A erhält den Namen „Vektorpotential“, ist aber nicht direkt mit der Arbeit verbunden, wie es das skalare Potential ist.
Das Vektorpotential ist definiert als konsistent mit dem Ampere-Gesetz und kann entweder als Strom i oder als Stromdichte j (die Quellen des Magnetfelds) ausgedrückt werden. In verschiedenen Texten nimmt diese Definition die Formen an
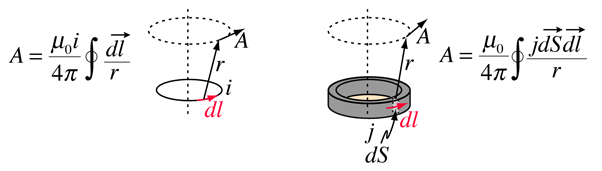
Eine Begründung für das Vektorpotential ist, dass es einfacher sein kann, das Vektorpotential zu berechnen, als das Magnetfeld direkt aus einer gegebenen Quellstromgeometrie zu berechnen. Seine häufigste Anwendung ist die Antennentheorie und die Beschreibung elektromagnetischer Wellen.
Da das Magnetfeld B als Wellung von A definiert ist und der durch den Vektor der Wellung eines Gradienten identische Null ist, kann jede beliebige Funktion, die als Gradient einer Skalarfunktion ausgedrückt werden kann, zu A addiert werden, ohne den daraus erhaltenen Wert von B zu ändern. Das heißt, A‘ kann frei durch A ersetzt werden, wobei
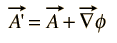
Solche Transformationen werden als Eichtransformationen bezeichnet, und es gab eine Reihe von „Messgeräten“, die für bestimmte Arten von Berechnungen in der elektromagnetischen Theorie vorteilhaft verwendet wurden.