Greedy algoritmus példákkal: Greedy Method & Approach

a kapzsi megközelítés megértéséhez a rekurzió és a kontextusváltás ismeretére van szükség. Ez segít megérteni, hogyan kell nyomon követni a kódot. A mohó paradigmát a saját szükséges és elégséges kijelentéseiddel határozhatod meg.

két feltétel határozza meg a kapzsi paradigmát.

• minden lépésenkénti megoldásnak a legjobban elfogadott megoldás felé kell strukturálnia a problémát.
• elegendő, ha a probléma strukturálása véges számú kapzsi lépésben megáll.

a teoretizálás folytatásával írjuk le a mohó Keresési megközelítéshez kapcsolódó történelmet.

ebben a kapzsi algoritmus bemutatóban megtudhatja:

• a kapzsi algoritmusok története
• kapzsi stratégiák és döntések
• a kapzsi megközelítés jellemzői
• miért használja a kapzsi megközelítést?
• hogyan lehet megoldani a tevékenység kiválasztási problémát
• a kapzsi megközelítés architektúrája
• a kapzsi algoritmusok hátrányai

a kapzsi algoritmusok története

itt található a kapzsi algoritmusok fontos mérföldköve:

• a mohó algoritmusokat az 1950-es években számos gráfjárási algoritmusra fogalmazták meg.
• Esdger Djikstra úgy fogalmazta meg az algoritmust, hogy minimális átívelő fákat generáljon. Célja az volt, hogy lerövidítse az útvonalak hosszát a holland fővárosban, Amszterdamban.
• ugyanebben az évtizedben Prim és Kruskal olyan optimalizálási stratégiákat ért el, amelyek a mérlegelt útvonalak útvonalköltségeinek minimalizálásán alapultak.
• a ‘ 70-es években amerikai kutatók, Cormen, Rivest és Stein a greedy megoldások rekurzív alszerkezetét javasolták Klasszikus Bevezetés Az algoritmusokba című könyvükben.
• a kapzsi Keresési paradigmát 2005-ben más típusú optimalizálási stratégiaként regisztrálták a NIST nyilvántartásaiban.
• a webet futtató protokollok, mint például az open-shortest-path-first (OSPF) és sok más hálózati csomagkapcsolási protokoll a greedy stratégiát használja a hálózaton töltött idő minimalizálására.

kapzsi stratégiák és döntések

a logika legegyszerűbb formájában “kapzsi” vagy “nem kapzsi”lett. Ezeket az állításokat az egyes algoritmus-szakaszok előrehaladásának megközelítése határozta meg.

például Djikstra algoritmusa egy lépésenkénti kapzsi stratégiát használt az interneten lévő gazdagépek azonosítására egy költségfüggvény kiszámításával. A költségfüggvény által visszaadott érték meghatározta, hogy a következő út “kapzsi” vagy “nem kapzsi”.

röviden: egy algoritmus megszűnik mohónak lenni, ha bármely szakaszban olyan lépést tesz, amely nem lokálisan mohó. A kapzsi problémák megállnak a kapzsiság további hatóköre nélkül.

a kapzsi megközelítés jellemzői

a kapzsi módszer algoritmusának fontos jellemzői:

• van egy rendezett lista az erőforrásokról, költségekkel vagy érték-hozzárendelésekkel. Ezek számszerűsítik a rendszer korlátait.
• az erőforrások maximális mennyiségét a korlátozás érvényességi ideje alatt veszi igénybe.
• például egy tevékenységütemezési probléma esetén az erőforrás-költségek órákban vannak megadva, és a tevékenységeket soros sorrendben kell végrehajtani.

miért használja a kapzsi megközelítést?

itt vannak a mohó megközelítés használatának okai:

• a kapzsi megközelítésnek van néhány kompromisszuma, amelyek alkalmassá tehetik az optimalizálásra.
• az egyik kiemelkedő ok az, hogy azonnal elérjük a leginkább megvalósítható megoldást. A tevékenységválasztási problémában (az alábbiakban ismertetjük), ha több tevékenységet lehet elvégezni az aktuális tevékenység befejezése előtt, akkor ezek a tevékenységek ugyanabban az időben elvégezhetők.
• egy másik ok a probléma rekurzív felosztása egy feltétel alapján, anélkül, hogy az összes megoldást össze kellene kapcsolni.
• a tevékenységválasztási problémában a “rekurzív felosztás” lépés úgy érhető el, hogy csak egyszer vizsgálja meg az elemek listáját, és figyelembe vesz bizonyos tevékenységeket.

hogyan lehet megoldani a tevékenységkiválasztási problémát

a tevékenységütemezési példában minden tevékenységhez “start” és “finish” idő tartozik. Minden tevékenységet referenciaként egy szám indexel. Két tevékenységi kategória létezik.

1. figyelembe vett tevékenység: az a tevékenység, amely az a referencia, amelyből egynél több fennmaradó tevékenység elvégzésének képességét elemzik.
2. fennmaradó tevékenységek: a vizsgált tevékenységet megelőző egy vagy több Indexen végzett tevékenységek.

a teljes időtartam megadja a tevékenység elvégzésének költségeit. Vagyis (Befejezés-indítás) megadja nekünk az időtartamot, mint egy tevékenység költségét.

meg fogja tanulni, hogy a mohó mértéke a fennmaradó tevékenységek száma, amelyeket a megfontolt tevékenység idején végezhet.

a kapzsi megközelítés architektúrája

1.lépés)

vizsgálja meg a tevékenységi költségek listáját, kezdve a 0. indexgel, mint a figyelembe vett Index.

2. lépés)

ha több tevékenység befejezhető az idő, a figyelembe vett tevékenység befejeződik, kezdje el keresni egy vagy több fennmaradó tevékenységet.

3. lépés)

ha nincs több hátralévő tevékenység, akkor az aktuális hátralévő tevékenység lesz a következő figyelembe vett tevékenység. Ismételje meg az 1.és a 2. lépést az új megfontolt tevékenységgel. Ha nem maradt más tevékenység, folytassa a 4. lépéssel.

4.lépés )

adja vissza a figyelembe vett indexek unióját. Ezek azok a tevékenységi indexek, amelyeket az áteresztőképesség maximalizálására használnak.

Kód magyarázat

#include<iostream>#include<stdio.h>#include<stdlib.h>#define MAX_ACTIVITIES 12

a kód magyarázata:

1. tartalmazza header fájlok / osztályok
2. a Max tevékenységek száma a felhasználó által biztosított.

using namespace std;class TIME{ public: int hours; public: TIME() { hours = 0; }};

a kód magyarázata:

1. a streaming műveletek névtere.
2. az idő osztálydefiníciója
3. egy órás időbélyeg.
4. a TIME default konstruktor
5. a hours változó.

class Activity{ public: int index; TIME start; TIME finish; public: Activity() { start = finish = TIME(); }};

a kód magyarázata:

1. osztálydefiníció activity
2. Timestamps időtartam meghatározása
3. minden időbélyeg 0-ra inicializálódik az alapértelmezett konstruktorban

class Scheduler{ public: int considered_index,init_index; Activity *current_activities = new Activity; Activity *scheduled;

a kód magyarázata:

1. az ütemező osztály definíciójának 1. része.
2. a vizsgált Index a tömb beolvasásának kiindulópontja.
3. az inicializálási index véletlenszerű időbélyegek hozzárendelésére szolgál.
4. tevékenységobjektumok tömbje dinamikusan kerül kiosztásra az új operátor segítségével.
5. az ütemezett mutató meghatározza a kapzsiság aktuális alaphelyét.

Scheduler(){ considered_index = 0; scheduled = NULL;......

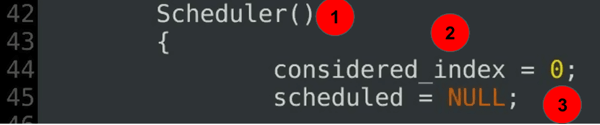
a kód magyarázata:

1. az ütemező konstruktor-az ütemező osztály definíciójának 2. része.
2. a vizsgált index határozza meg az aktuális vizsgálat aktuális kezdetét.
3. a jelenlegi mohó mérték az elején nincs meghatározva.

for(init_index = 0; init_index < MAX_ACTIVITIES; init_index++) { current_activities.start.hours = rand() % 12; current_activities.finish.hours = current_activities.start.hours + (rand() % 2); printf("\nSTART:%d END %d\n", current_activities.start.hours ,current_activities.finish.hours); }……

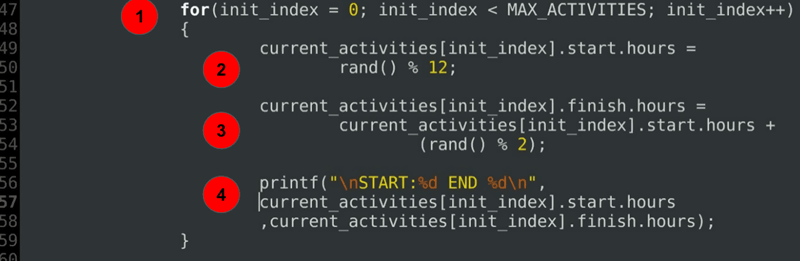
a kód magyarázata:

1. a ciklus az egyes ütemezett tevékenységek kezdő és záró óráinak inicializálására.
2. kezdési idő inicializálása.
3. befejezési idő inicializálás mindig a kezdési óra után vagy pontosan.
4. hibakeresési utasítás A kiosztott időtartamok kinyomtatásához.

public: Activity * activity_select(int);};

a kód magyarázata:

1. 4. rész – az ütemező osztály definíciójának utolsó része.
2. az Activity select függvény egy kiindulási pont indexet vesz alapul, és a greedy küldetést kapzsi részproblémákra osztja.

Activity * Scheduler :: activity_select(int considered_index){ this->considered_index = considered_index; int greedy_extent = this->considered_index + 1;…… 

1. a scope resolution operátor (::) használatával a függvény meghatározása biztosított.
2. a figyelembe vett Index az érték által hívott Index. A greedy_extent az inicializált csak egy index a figyelembe vett Index után.

Activity * Scheduler :: activity_select(int considered_index){ while( (greedy_extent < MAX_ACTIVITIES ) && ((this->current_activities).start.hours < (this->current_activities).finish.hours )) { printf("\nSchedule start:%d \nfinish%d\n activity:%d\n", (this->current_activities).start.hours, (this->current_activities).finish.hours, greedy_extent + 1); greedy_extent++; }…...

a kód magyarázata:

1. az alapvető logika – a kapzsi mértékben korlátozódik a tevékenységek száma.
2. az aktuális tevékenység kezdő óráit ütemezhetőként ellenőrzik, mielőtt a figyelembe vett tevékenység (a figyelembe vett index által megadva) befejeződne.
3. amíg ez lehetséges, egy opcionális hibakeresési utasítás nyomtatásra kerül.
4. előre a következő index a tevékenység tömb

...if ( greedy_extent <= MAX_ACTIVITIES ) { return activity_select(greedy_extent); } else { return NULL; }}

a kód magyarázata:

1. a feltételes ellenőrzések, ha az összes tevékenységet lefedték.
2. ha nem, akkor újraindíthatja a greedy – t, ha a figyelembe vett Index az aktuális pont. Ez egy rekurzív lépés, amely mohón osztja a problémamegállapítást.
3. ha igen, visszatér a hívóhoz, anélkül, hogy kiterjesztené a kapzsiságot.

int main(){ Scheduler *activity_sched = new Scheduler(); activity_sched->scheduled = activity_sched->activity_select( activity_sched->considered_index); return 0;}

a kód magyarázata:

1. az ütemező meghívására használt fő funkció.
2. egy új ütemező példányosul.
3. az activity select függvény, amely egy activity típusú mutatót ad vissza, visszatér a hívóhoz, miután a kapzsi küldetés véget ért.

kimenet:

START:7 END 7START:9 END 10START:5 END 6START:10 END 10START:9 END 10Schedule start:5 finish6 activity:3Schedule start:9 finish10 activity:5

a mohó algoritmusok hátrányai

nem alkalmas olyan mohó problémákra, ahol minden alproblémához, például a rendezéshez, megoldásra van szükség.

ilyen mohó algoritmus gyakorlati problémákban a mohó módszer hibás lehet; a legrosszabb esetben még nem optimális megoldáshoz is vezethet.

ezért a kapzsi algoritmusok hátránya, hogy nem tudják, mi áll a jelenlegi kapzsi állapot előtt.

az alábbiakban bemutatjuk a kapzsi módszer hátrányát:

az itt faként (magasabb érték magasabb kapzsiság) bemutatott kapzsi letapogatásban egy algoritmus állapot értéke: 40, valószínűleg 29 lesz a következő érték. Továbbá a küldetés 12-kor ér véget. Ez az érték 41.

Ha azonban az algoritmus nem optimális utat választott, vagy hódító stratégiát fogadott el. ezután 25-öt követ 40, az Általános költségjavulás pedig 65 lenne, amelyet 24 ponttal magasabbra értékelnek, mint nem optimális döntést.

példák a kapzsi algoritmusokra

a legtöbb hálózati algoritmus a kapzsi megközelítést használja. Itt található néhány kapzsi algoritmus példa:

• Prim minimális átívelő fa algoritmus
• utazó eladó probléma
• Graph – Térkép színezés
• Kruskal minimális átívelő fa algoritmus
• Dijkstra minimális átívelő fa algoritmus
• Graph – csúcs borító
• hátizsák probléma
• feladatütemezési probléma

Összegzés:

összefoglalva, A cikk meghatározta a kapzsi paradigmát, megmutatta, hogy a kapzsi optimalizálás és rekurzió hogyan segíthet a legjobb megoldás elérésében egy pontig. A kapzsi algoritmus széles körben alkalmazzák a problémamegoldás számos nyelven kapzsi algoritmus Python, C, C#, PHP, Java, stb. A mohó algoritmus példájának tevékenységválasztását stratégiai problémaként írták le, amely a mohó megközelítéssel maximális teljesítményt érhet el. Végül elmagyarázták a kapzsi megközelítés használatának hátrányait.