CONDUCIBILITÀ TERMICA

La conduttività termica dei solidi è di natura diversa a seconda che siano o meno conduttori. Nei dielettrici senza cariche elettriche libere, l’energia termica viene trasferita dai fononi. Le vibrazioni collettive degli atomi nel reticolo cristallino assumono la forma di onde di spostamento, la cui interferenza genera pacchetti d’onda, cioè fononi. Le onde di spostamento provocano fluttuazioni di densità che possono manifestarsi come variazione dell’indice di rifrazione. Se le onde passano attraverso una regione in cui l’indice di rifrazione differisce dal valore volumetrico medio, le successive onde di spostamento che trasportano l’energia del moto termico saranno disperse.

La dispersione è più forte, più la deviazione massima degli atomi dalle loro posizioni medie nel reticolo, cioè più alta è la T. Ciò spiega il fatto accertato sperimentalmente che la conduttività termica dei dielettrici cristallini diminuisce a temperature abbastanza elevate: λ 1/T (Figura 1).

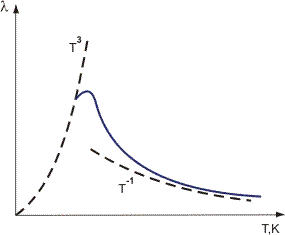
Figura 1. Variazione della conducibilità termica dei dielettrici cristallini con la temperatura.

Debye ha dato una panoramica di un carattere peaklike di λ(T) variazione a bassa T nel quadro dei concetti di meccanica quantistica. Ha elaborato una teoria dei dipoli dei dielettrici basata sul concetto di una molecola come dipolo rigido. In questo modello Debye introdusse il concetto della cosiddetta temperatura di Debye θD proporzionale alla frequenza massima delle vibrazioni atomiche in un solido. Per la maggior parte delle sostanze θD è inferiore o vicino alla temperatura ambiente (un’eccezione è diamante per cui θD = 1850 K e berrylium per cui θD = 1160K).

In teoria quantistica dei solidi, il reticolo cristallino è considerato come un volume riempito con phonon di gas per cui la detrazione del più semplice la teoria cinetica viene applicato

dove c è la capacità termica di un materiale dielettrico che coincide con quella di phonon gas, v la velocità media di fononi circa uguale alla velocità del suono,il libero cammino medio dei fononi. L’esistenza di un certo valore finito di è il risultato dello scattering dei fononi sui fononi, sui difetti del reticolo cristallino e, in particolare, sui confini del grano sull’intero campione. La dipendenza della temperatura λ (T) è determinata da quella die c sulla temperatura.

Ad alte temperature che superano sostanzialmente la temperatura di Debye θD, il meccanismo di base che limita è uno scattering fonone-fonone dovuto all’anarmonicità delle vibrazioni atomiche in un cristallo. Il meccanismo fonone-fonone di resistenza termica ((1/λ) è noto come coefficiente di resistenza termica) è fattibile solo a causa di una transizione con conseguente ritardo del flusso fononico e modifica apprezzabile del quasi-momento. Maggiore è la T, maggiore è la probabilità della transizione condecrescente:(1/T). Poiché a T > θD la capacità termica c aumenta solo leggermente con la temperatura, quindi λ 1/T.

A temperature inferiori alla temperatura di Debye, T<<θD, la lunghezza del cammino libero mediodeterminato dal fonone-fonone dispersione aumenta drasticamente,expθD/T e, come regola, è confinato in una dimensione di cristallo R. Secondo la legge di Debye capacità termica c in questo range di temperatura varia come c(T/θD)3. Di conseguenza, a T → 0 il coefficiente di conducibilità termica λ deve diminuire in proporzione a T3. La temperatura per la quale la conducibilità termica ha un picco è determinata da≈ R, che corrisponde comunemente a T ≤ 0,05 θD.

Questa teoria spiega anche il comportamento del coefficiente di conduttività termica per sostanze amorfe che non hanno un ordine a lungo raggio, cioè la dimensione dei loro “cristalli” è dell’ordine delle dimensioni atomiche. In virtù di ciò, la dispersione ai “confini” di queste sostanze deve prevalere in tutti i T e≈ const. Il coefficiente di conducibilità termica delle sostanze amorfe λ T3 a basse temperature e deve crescere leggermente, in proporzione alla capacità termica, a temperature moderate e alte, T > θD.

Tutto ciò fornisce una spiegazione qualitativa della dipendenza λ(T) nei dielettrici cristallini reali, ma non tiene conto delle deviazioni dal reticolo costante dovute alle impurità atomiche di altri elementi e dei loro isotopi. Ad una temperatura elevata la resistenza che è offerta dalle impurità al trasporto di calore è indipendente dalla temperatura. Ciò consente di stimare il grado di purezza del cristallo dalla variazione della sua conduttività termica con la temperatura. Lo stesso fatto ci consente di determinare la distribuzione tra sostanza vetrosa e cristallina nel minerale naturale se il vetro è considerato come un’impurità in un cristallo.

La conduttività termica nei metalli dipende dal movimento e dall’interazione dei portatori di corrente, cioè gli elettroni di conduzione. Generalmente, il coefficiente di conducibilità termica λ di un metallo è uguale alla somma del reticolo (fonone) λph e dei componenti λe dell’elettrone, λ = λe + λph; a temperature ordinarie, di regola, λe >>λph.

Se applichiamo una semplice teoria cinetica dei gas al flusso di elettroni liberi e supponiamo che la lunghezza del loro percorso libero non dipenda dalla velocità, allora la teoria implica che

dove e è la carica dell’elettrone, la costante di K Boltzrnann e σ la conduttività elettrica. Una stretta di meccanica quantistica, la teoria offre una simile relazione,

In entrambe le formule, il rapporto dell’elettrone parte del coefficiente di conducibilità termica λ per la conducibilità elettrica σ, in un ampio intervallo di temperatura, sembra essere in proporzione alla temperatura secondo la Wiedemann-Franz legge, λ/σ = L, dove L è il numero di Lorentz. Questa legge viene utilizzata per calcolare λe dalla conduttività elettrica misurata. Tuttavia, viene violato a temperature inferiori a θD quando prevale un’interazione elettrone-fonone (σ cresce con la diminuzione di T come T−5 mentre le varia più leggermente come T−2).

I risultati sperimentali dimostrano che, di norma, la conduttività termica dei metalli ad alte temperature è una funzione leggermente decrescente della temperatura. Ma ci sono molte eccezioni. Pertanto, la conduttività termica del ferro diminuisce fortemente con la temperatura mentre il tantalio e il niobio mostrano un coefficiente di temperatura positivo.

Di interesse sono i tentativi di confrontare i coefficienti di conducibilità termica per diverse sostanze per una singola temperatura caratteristica, ad esempio per il punto di fusione Tm dei solidi. Pertanto, il trattamento statistico dei dati sperimentali svolte da Missenard ha dimostrato che la conducibilità termica dei metalli al punto di fusione λ(T = Tm) = λm è in proporzione λe conducibilità termica del dielettrico cristalli a T = Tm è in proporzione, dove m è la massa molecolare, N il numero di atomi nella formula chimica, ρ la densità e il punto di fusione Tm è in gradi Kelvin.

Il trasporto di calore nei semiconduttori è più complesso che nei dielettrici e nei metalli perché il fonone e i componenti elettronici sono ugualmente essenziali per loro. Un altro motivo della complessità è il notevole effetto delle impurità, della diffusione bipolare e di altri fattori poco studiati sul trasferimento di calore.

L’effetto della pressione sulla conduttività termica dei solidi può essere assunto, con una buona precisione, come lineare, λ per molti metalli che crescono con p.

Per l’effetto della porosità sulla conduttività termica dei solidi vedi Mezzo poroso.