
In questo post, impareremo i dettagli dell’istogramma del descrittore di gradienti orientati (HOG). Impareremo cosa c’è sotto il cofano e come questo descrittore è calcolato internamente da OpenCV, MATLAB e altri pacchetti.
Questo post fa parte di una serie che sto scrivendo sul riconoscimento delle immagini e sul rilevamento degli oggetti.
L’elenco completo dei tutorial di questa serie è riportato di seguito:
- Riconoscimento delle immagini con tecniche tradizionali di visione artificiale : Parte 1
- Istogramma dei Orientato Gradienti : Parte 2
- codice di Esempio per il riconoscimento di immagini : Parte 3
- la Formazione di un occhio migliore del rivelatore: Parte 4a
- rilevamento di Oggetti utilizzando le tradizionali tecniche di Computer Vision : Parte 4b
- Come allenarsi e testare le tue OpenCV oggetto rivelatore : Parte 5
- riconoscimento dell’Immagine, l’utilizzo di Deep Learning : Parte 6
- Introduzione alle reti neurali
- Comprensione delle reti neurali feedforward
- Riconoscimento delle immagini mediante reti neurali convoluzionali
- Rilevamento di oggetti con apprendimento profondo: Parte 7
Molte cose sembrano difficili e misteriose. Ma una volta che si prende il tempo per decostruirli, il mistero è sostituito dalla maestria e questo è ciò che stiamo cercando. Se sei un principiante e stai trovando la visione artificiale difficile e misteriosa, ricorda quanto segue
D: Come mangi un elefante ?
A : Un morso alla volta!
- Che cos’è un descrittore di funzionalità?
- Come calcolare l’istogramma dei gradienti orientati ?
- Fase 1 : Pre-elaborazione
- Passo 2: Calcolare le immagini del gradiente
- Passo 3: Calcola Istogramma di gradienti in 8×8 celle
- Fase 4 : 16×16 Blocco Normalizzazione
- Passo 5 : Calcola il vettore di funzionalità HOG
- Visualizzazione istogramma di gradienti orientati
- Iscriviti & Scarica il codice
Che cos’è un descrittore di funzionalità?
Un descrittore di funzionalità è una rappresentazione di un’immagine o di una patch di immagine che semplifica l’immagine estraendo informazioni utili e gettando via informazioni estranee.
In genere, un descrittore di funzionalità converte un’immagine di dimensioni larghezza x altezza x 3 (canali ) in un vettore di funzionalità / array di lunghezza n. Nel caso del descrittore di funzionalità HOG, l’immagine di input è di dimensioni 64 x 128 x 3 e il vettore di funzionalità di output è di lunghezza 3780.
Tieni presente che il descrittore di HOG può essere calcolato per altre dimensioni, ma in questo post mi attengo ai numeri presentati nel documento originale in modo da poter comprendere facilmente il concetto con un esempio concreto.
Tutto questo suona bene, ma cosa è “utile” e cosa è “estraneo”? Per definire “utile”, dobbiamo sapere a cosa serve” utile”? Chiaramente, il vettore di funzionalità non è utile allo scopo di visualizzare l’immagine. Ma è molto utile per compiti come il riconoscimento delle immagini e il rilevamento degli oggetti. Il vettore di funzionalità prodotto da questi algoritmi quando inserito in un algoritmo di classificazione delle immagini come Support Vector Machine (SVM) produce buoni risultati.
Ma quali tipi di” caratteristiche ” sono utili per le attività di classificazione ? Discutiamo questo punto usando un esempio. Supponiamo di voler costruire un rilevatore di oggetti che rilevi bottoni di camicie e cappotti.
Un pulsante è circolare (può sembrare ellittico in un’immagine) e di solito ha alcuni fori per cucire. È possibile eseguire un rivelatore bordo sull’immagine di un pulsante, e facilmente dire se si tratta di un pulsante semplicemente guardando l’immagine bordo da solo. In questo caso, le informazioni sul bordo sono “utili” e le informazioni sul colore no. Inoltre, le caratteristiche devono anche avere potere discriminatorio. Ad esempio, le buone caratteristiche estratte da un’immagine dovrebbero essere in grado di distinguere tra pulsanti e altri oggetti circolari come monete e pneumatici per auto.
Nel descrittore di funzionalità HOG, la distribuzione ( istogrammi ) delle direzioni dei gradienti ( gradienti orientati ) viene utilizzata come funzionalità. I gradienti (derivati x e y ) di un’immagine sono utili perché la grandezza dei gradienti è grande intorno ai bordi e agli angoli ( regioni di bruschi cambiamenti di intensità) e sappiamo che i bordi e gli angoli contengono molte più informazioni sulla forma dell’oggetto rispetto alle regioni piatte.
Come calcolare l’istogramma dei gradienti orientati ?
In questa sezione, andremo nei dettagli del calcolo del descrittore di funzionalità HOG. Per illustrare ogni passaggio, useremo una patch di un’immagine.
Fase 1 : Pre-elaborazione
Come accennato in precedenza HOG caratteristica descrittore utilizzato per il rilevamento pedonale è calcolato su un 64×128 patch di un’immagine. Naturalmente, un’immagine può essere di qualsiasi dimensione. In genere le patch su più scale vengono analizzate in molte posizioni dell’immagine. L’unico vincolo è che le patch analizzate hanno un rapporto di aspetto fisso. Nel nostro caso, le patch devono avere un rapporto di aspetto di 1: 2. Ad esempio, possono essere 100×200, 128×256 o 1000×2000 ma non 101×205.
Per illustrare questo punto ho mostrato una grande immagine di dimensioni 720×475. Abbiamo selezionato una patch di dimensioni 100×200 per calcolare il nostro descrittore di funzionalità HOG. Questa patch viene ritagliata da un’immagine e ridimensionata a 64×128. Ora siamo pronti a calcolare il descrittore di HOG per questa patch di immagine.

Il documento di Dalal e Triggs menziona anche la correzione gamma come fase di pre-elaborazione, ma i guadagni in termini di prestazioni sono minori e quindi stiamo saltando il passaggio.
Passo 2: Calcolare le immagini del gradiente
Per calcolare un descrittore di MAIALE, dobbiamo prima calcolare i gradienti orizzontali e verticali; dopo tutto, vogliamo calcolare l’istogramma dei gradienti. Questo si ottiene facilmente filtrando l’immagine con i seguenti kernel.
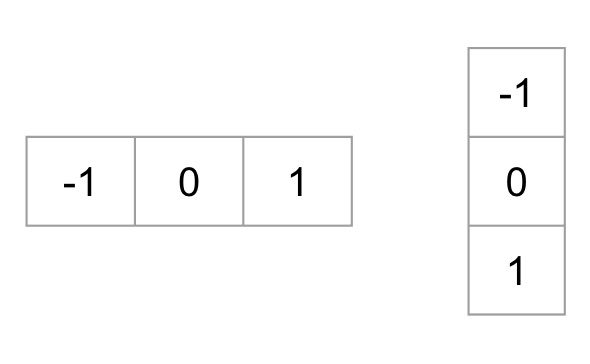
Possiamo anche ottenere gli stessi risultati, usando l’operatore Sobel in OpenCV con la dimensione del kernel 1.
// C++ gradient calculation.// Read imageMat img = imread("bolt.png");img.convertTo(img, CV_32F, 1/255.0);// Calculate gradients gx, gyMat gx, gy;Sobel(img, gx, CV_32F, 1, 0, 1);Sobel(img, gy, CV_32F, 0, 1, 1);
# Python gradient calculation # Read imageim = cv2.imread('bolt.png')im = np.float32(im) / 255.0# Calculate gradientgx = cv2.Sobel(img, cv2.CV_32F, 1, 0, ksize=1)gy = cv2.Sobel(img, cv2.CV_32F, 0, 1, ksize=1)
a quel punto, siamo in grado di trovare la grandezza e la direzione del gradiente utilizzando la seguente formula

Se si utilizza la libreria OpenCV, il calcolo può essere fatto utilizzando la funzione cartToPolar come mostrato di seguito.
// C++ Calculate gradient magnitude and direction (in degrees)Mat mag, angle;cartToPolar(gx, gy, mag, angle, 1);
Lo stesso codice in python è simile a questo.
# Python Calculate gradient magnitude and direction ( in degrees )mag, angle = cv2.cartToPolar(gx, gy, angleInDegrees=True)
La figura seguente mostra i gradienti.
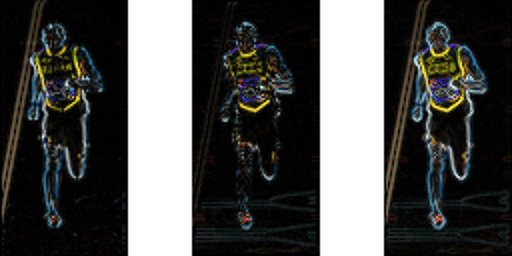
Si noti che il gradiente x si attiva su linee verticali e il gradiente y su linee orizzontali. La grandezza degli incendi gradiente dove mai c’è un brusco cambiamento di intensità. Nessuno di loro spara quando la regione è liscia. Ho deliberatamente lasciato fuori l’immagine che mostra la direzione del gradiente perché la direzione mostrata come immagine non trasmette molto.
L’immagine del gradiente ha rimosso molte informazioni non essenziali ( ad esempio sfondo colorato costante ), ma ha evidenziato i contorni. In altre parole, puoi guardare l’immagine del gradiente e dire facilmente che c’è una persona nell’immagine.
Ad ogni pixel, il gradiente ha una magnitudine e una direzione. Per le immagini a colori, vengono valutati i gradienti dei tre canali (come mostrato nella figura sopra ). La grandezza del gradiente in un pixel è il massimo della grandezza dei gradienti dei tre canali e l’angolo è l’angolo corrispondente al gradiente massimo.
Passo 3: Calcola Istogramma di gradienti in 8×8 celle

In questo passaggio, l’immagine viene divisa in 8×8 celle e viene calcolato un istogramma di gradienti per ogni 8×8 celle.
Impareremo a conoscere gli istogrammi in un momento, ma prima di andare lì capiamo prima perché abbiamo diviso l’immagine in 8×8 celle. Uno dei motivi importanti per utilizzare un descrittore di funzionalità per descrivere una patch di un’immagine è che fornisce una rappresentazione compatta. Una patch immagine 8×8 contiene 8x8x3 = 192 valori di pixel. Il gradiente di questa patch contiene 2 valori (magnitudine e direzione) per pixel che aggiunge fino a 8x8x2 = 128 numeri.
Alla fine di questa sezione vedremo come questi 128 numeri sono rappresentati utilizzando un istogramma 9-bin che può essere memorizzato come una matrice di 9 numeri. Non solo la rappresentazione è più compatta, il calcolo di un istogramma su una patch rende questa rappresentazione più robusta al rumore. I singoli graidents possono avere rumore, ma un istogramma su 8×8 patch rende la rappresentazione molto meno sensibile al rumore.
Ma perché 8×8 patch ? Perché non 32×32 ? Si tratta di una scelta di design informata dalla scala di caratteristiche che stiamo cercando. HOG è stato utilizzato inizialmente per il rilevamento dei pedoni. Le celle 8×8 in una foto di un pedone ridimensionate a 64×128 sono abbastanza grandi da catturare caratteristiche interessanti (ad esempio il viso, la parte superiore della testa ecc. ).
L’istogramma è essenzialmente un vettore (o una matrice) di 9 bin (numeri ) corrispondenti agli angoli 0, 20, 40, 60 … 160.
Diamo un’occhiata a una patch 8×8 nell’immagine e vediamo come appaiono i gradienti.
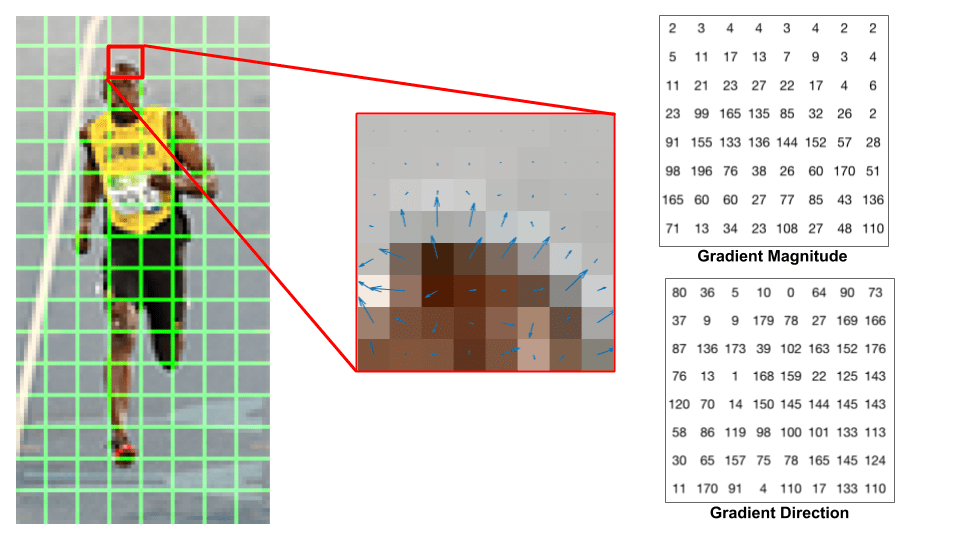
Se sei un principiante in computer vision, l’immagine al centro è molto istruttiva. Mostra la patch dell’immagine sovrapposta con le frecce che mostrano il gradiente – la freccia mostra la direzione del gradiente e la sua lunghezza mostra la grandezza. Si noti come la direzione delle frecce indica la direzione del cambiamento di intensità e la grandezza mostra quanto è grande la differenza.
A destra, vediamo i numeri grezzi che rappresentano i gradienti nelle celle 8×8 con una differenza minore: gli angoli sono compresi tra 0 e 180 gradi anziché tra 0 e 360 gradi. Questi sono chiamati gradienti “senza segno” perché un gradiente ed è negativo sono rappresentati dagli stessi numeri. In altre parole, una freccia sfumata e quella opposta di 180 gradi sono considerate uguali. Ma, perché non usare i gradi 0 – 360 ?
Empiricamente è stato dimostrato che i gradienti non firmati funzionano meglio dei gradienti firmati per il rilevamento dei pedoni. Alcune implementazioni di HOG ti permetteranno di specificare se vuoi usare i gradienti firmati.
Il passo successivo è creare un istogramma di gradienti in queste celle 8×8. L’istogramma contiene 9 bidoni corrispondenti agli angoli 0, 20, 40 … 160. La figura seguente illustra il processo. Stiamo guardando la grandezza e la direzione del gradiente della stessa patch 8×8 come nella figura precedente.
Un bin viene selezionato in base alla direzione e il voto ( il valore che va nel bin ) viene selezionato in base alla grandezza. Concentriamoci prima sul pixel circondato in blu. Ha un angolo (direzione ) di 80 gradi e magnitudine di 2. Quindi aggiunge 2 al 5 ° cestino. Il gradiente al pixel circondato usando il rosso ha un angolo di 10 gradi e una magnitudine di 4. Poiché 10 gradi è a metà strada tra 0 e 20, il voto del pixel si divide uniformemente nei due bidoni.
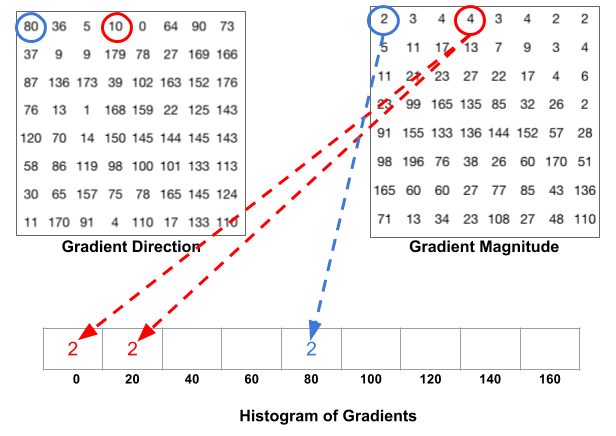
C’è un altro dettaglio di cui essere a conoscenza. Se l’angolo è maggiore di 160 gradi, è compreso tra 160 e 180, e sappiamo che l’angolo si avvolge facendo 0 e 180 equivalenti. Quindi, nell’esempio seguente, il pixel con angolo di 165 gradi contribuisce proporzionalmente al contenitore di 0 gradi e al contenitore di 160 gradi.
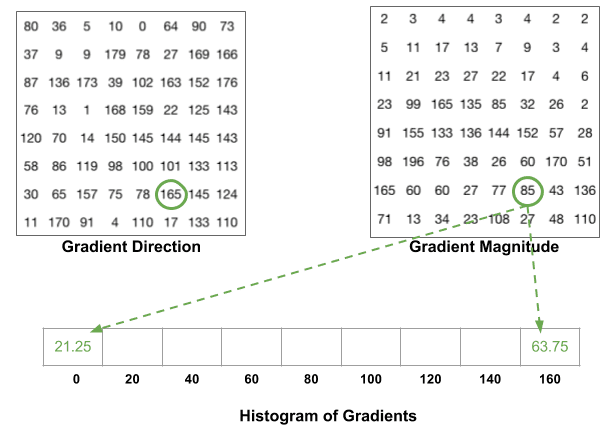
I contributi di tutti i pixel nelle celle 8×8 vengono sommati per creare l’istogramma 9-bin. Per la patch di cui sopra, sembra che questo
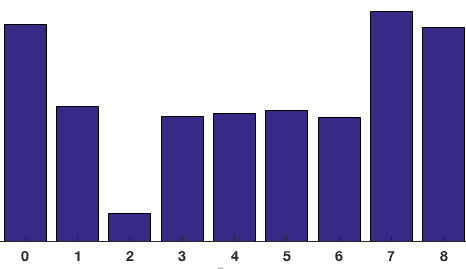
Nella nostra rappresentazione, l’asse y è 0 gradi. Puoi vedere che l’istogramma ha un sacco di peso vicino a 0 e 180 gradi, che è solo un altro modo per dire che nella patch i gradienti puntano verso l’alto o verso il basso.
Fase 4 : 16×16 Blocco Normalizzazione
Nel passaggio precedente, abbiamo creato un istogramma basato sul gradiente dell’immagine. I gradienti di un’immagine sono sensibili all’illuminazione generale. Se si rende l’immagine più scura dividendo tutti i valori dei pixel per 2, la grandezza del gradiente cambierà della metà e quindi i valori dell’istogramma cambieranno della metà.
Idealmente, vogliamo che il nostro descrittore sia indipendente dalle variazioni di illuminazione. In altre parole, vorremmo “normalizzare” l’istogramma in modo che non siano influenzati dalle variazioni di illuminazione.
Prima di spiegare come viene normalizzato l’istogramma, vediamo come viene normalizzato un vettore di lunghezza 3.
Diciamo che abbiamo un vettore di colore RGB . La lunghezza di questo vettore è $\sqrt{128^2 + 64^2 + 32^2} = 146.64$. Questa è anche chiamata la norma L2 del vettore. Dividendo ogni elemento di questo vettore per 146.64 ci dà un vettore normalizzato .
Consideriamo ora un altro vettore in cui gli elementi sono il doppio del valore del primo vettore 2 x = . Puoi risolverlo da solo per vedere che la normalizzazione si tradurrà in , che è la stessa della versione normalizzata del vettore RGB originale. Puoi vedere che la normalizzazione di un vettore rimuove la scala.
Ora che sappiamo come normalizzare un vettore, potresti essere tentato di pensare che mentre calcoli HOG puoi semplicemente normalizzare l’istogramma 9×1 allo stesso modo in cui abbiamo normalizzato il vettore 3×1 sopra. Non è una cattiva idea, ma un’idea migliore è quella di normalizzare su un blocco di dimensioni maggiori di 16×16.
Un blocco 16×16 ha 4 istogrammi che possono essere concatenati per formare un vettore di elementi 36 x 1 e possono essere normalizzati proprio come un vettore 3×1 viene normalizzato. La finestra viene quindi spostata di 8 pixel (vedi animazione) e un vettore normalizzato 36×1 viene calcolato su questa finestra e il processo viene ripetuto.
Passo 5 : Calcola il vettore di funzionalità HOG
Per calcolare il vettore di funzionalità finale per l’intera patch dell’immagine, i vettori 36×1 sono concatenati in un vettore gigante. Qual è la dimensione di questo vettore ? Calcoliamo
- Quante posizioni dei blocchi 16×16 abbiamo ? Ci sono 7 posizioni orizzontali e 15 verticali per un totale di 7 x 15 = 105 posizioni.
- Ogni blocco 16×16 è rappresentato da un vettore 36×1. Quindi quando li concateniamo tutti in un unico vettore gaint otteniamo un vettore dimensionale 36×105 = 3780.
Visualizzazione istogramma di gradienti orientati

Il descrittore HOG di una patch di immagine viene solitamente visualizzato tracciando gli istogrammi normalizzati 9×1 nelle celle 8×8. Vedi immagine a lato. Noterai che la direzione dominante dell’istogramma cattura la forma della persona, specialmente intorno al busto e alle gambe.
Sfortunatamente, non esiste un modo semplice per visualizzare il descrittore di HOG in OpenCV.