編集者注:Tony Abbeyは、米国、ヨーロッパ、アジアでライブNAFEMS FEAクラスを教えています。 また、NAFEMS e-learningクラスを世界的に教えています。 連絡先詳細については。
以前のデスクトップエンジニアリングの記事(“平面対称性を使用したFEAシミュレーションモデルの単純化”)では、強力な現代のコンピュータであっても、構造有限要素解析(FEA)で単純化技術を使用する動機があることが多いと説明しています。 このフォローアップでは、2つの密接に関連する方法を使用して、関心領域で複雑な構造を介して2Dスライスを取得する方法について説明します。 結果として得られるFEAモデルは、完全な3Dモデルよりも迅速かつ効率的に局所応力に関する貴重な洞察を与えることができます。 彼らは全体の話をすることはありませんが、CAEエンジニアのための貴重なツールです。
二つのFEA法は、平面応力と平面ひずみと呼ばれています。 どちらも、薄いシェル要素のように見える2D平面要素を使用し、平面サーフェスジオメトリを使用してメッシュされます。
平面応力解析
図。 図1に、平面応力解析に関する重要な事実を示します。 構造領域は、第三の構造寸法が比較的小さい、2D xy平面内にあると仮定される。 図では、これはz方向の厚さです。 応力は、σ x、σ y（直接応力）およびσ xy（平面内せん断応力）として2D平面に存在します。 これらの圧力のそれぞれは差込みに示されているように厚さによって一定している。 さらに、z方向に応力が発生することはありません。 この応力-ひずみ材料の関係は、このタイプの解析で使用される2次元平面応力要素で定義されます。
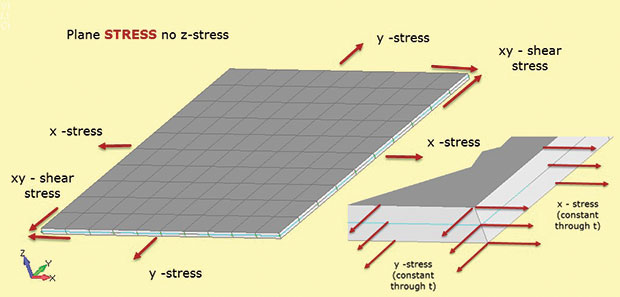1:平面の圧力;圧力の状態の仮定。z応力の欠如は、要素タイプの指定平面応力（すなわち、平面内応力のみが許容される）を覚えておく方法です。 厚さのせん断応力を介してもありません。 平面応力モデルを図1にロードできます。 また、対応する面内ひずみe-xおよびe-yを計算することもできます。 興味深いことに、貫通厚さひずみe-zを計算することもできます。xとyで伸びるにつれて、モデルはzで自由に薄くなるため、これはゼロではありません。 いくつかのソルバーでは、貫通厚さひずみe-zを回復し、それを使用して厚さの変化を計算することができます。 （モデルが二軸圧縮にあればzセクションはより厚くなります）。 これは通常、二次ひずみとみなされ、出力には使用できない場合がありますが、そこにあり、必要に応じて手動で計算することができます。
図2は、アルミニウムラグ成分を示す。 ラグナットはタング（か足）および下半身セクションに置かれ、結ばれる層がある合成シートのレイアップから突出する。 唐は合成の構造にラグナットに加えられる負荷を移す。 実際には、プライは、結合を通って複合体への滑らかなせん断移動を可能にするように階段状にされるであろう。 複合材料へのせん断移動は，タンに”引っ張る”拡散表面牽引力によってシミュレートされる。 これらは応用ラグナットの負荷のバランスをとる。
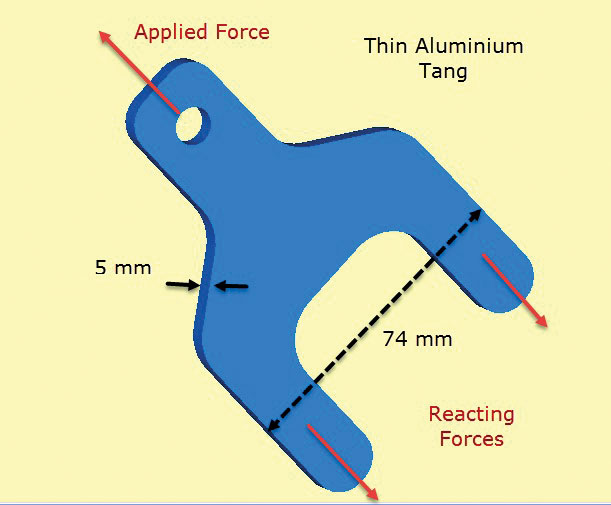2: 合成の構造への薄囲まれたアルミニウム唐の移動の負荷。ここで重要な仮定は、貫通厚さ応力がゼロであり、面内応力がコンポーネント内の貫通厚さが一定であるということです。 これは、複合材から唐材へのせん断荷重伝達の局所的な詳細がモデル化されていないことを意味します。 しかし，この解析の焦点は，面内応力を用いて，複合材の明確なラグとタング断面のサイジングをチェックすることである。
部品の厚さは他の寸法に比べて小さい。 この値は、平面応力要素定義の実際の厚さとして入力されます。
図3は、FEAモデルと計算された最大主応力を示しています。 関心のある領域は、ラグと肩の半径の周りにあります。 現実の世界では、応力集中における応力状態は3Dであり、厚さシグマz応力とせん断応力は局所的にバランスをとるでしょう。 しかし、ここでは、面内応力が支配的であると仮定することは非常に合理的です。 これは、ハンドブックに見られるほとんどの伝統的な応力集中（Kt）計算で暗黙の同じ仮定です。
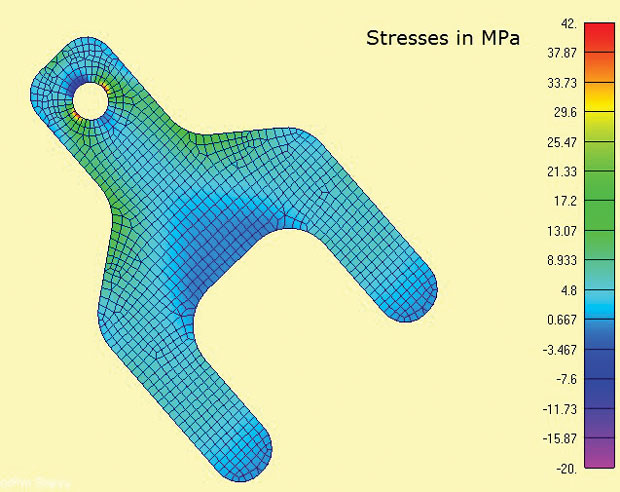図3:最大主応力を示す2D平面応力要素平面応力解析の便利な特徴の一つは、厳密に2D解析であるため、DOF(DOF)を制約する必要があることである(面内平行移動x、y、z軸周りの回転)。 これは、バランスのとれた負荷を持つ3-2-1最小制約法に適しています。 2次元の場合、これは2-1の方法に縮退する。 1つのノードはDOF xとyが制約され、2つ目の適切な直交ノードはDOF xが制約されています。 これにより、タング内の反応負荷を拡散分散負荷として直接適用することができます。 この境界条件を地面への制約を介してシミュレートすることは困難です。
貫通厚さe-zひずみ、したがってtangの薄肉化は、二次効果として計算することができます。
平面ひずみ解析
図。 図4は、平面ひずみ法の本質を示しています。 ここでも、2D平面要素が使用されますが、微妙に異なる仮定があります。 面内応力ｘ，ｙおよびｘｙは以前と同様に発達した。 しかし、今回はゼロに設定されている面外、またはthrough thickness z strainです。 したがって、平面ひずみ解析では、平面内のひずみのみが許可されます。 これは、示されているような厚い構造を表現するのに適しています。 この多くの材料の存在は部品を安定させ、zで緊張することを防ぎがちである。 この応力-ひずみ材料の関係は、このタイプの解析で使用される2次元平面ひずみ要素で定義されます。
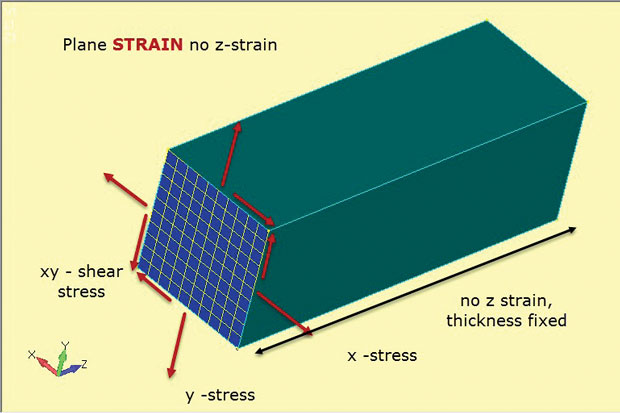図4:平面ひずみ解析;応力およびひずみ状態の仮定。図は、典型的な深い成分を介した切断部としての2D平面ひずみ要素の向きを示しています。 この切断部での応力状態は、成分を通る任意のxy平面切断（zステーション）で複製されるという仮定がある。 コンポーネントは、その長さの下に角柱（一定の断面を有する）であると仮定される。
実際には、深い成分の応力状態が平面から平面にゆっくりと変化するこの方法を使用します。 貫通厚さの歪みを安定させて除去するのに十分な材料が深さにあるはずです。 これは、図1に示す破壊靭性試験片で使用された原理と同じです。 5. 厚い試験片の中心部について，平面strain条件下での破壊を示した。 自由端と薄い断面での破壊は、より多くの平面応力状態のような、異なるモードです。 平面ひずみFEAモデルは、定義上、中心線の厚い試験片の挙動を良好に表現しますが、自由端または薄い試験片の挙動を表現するものではありません。
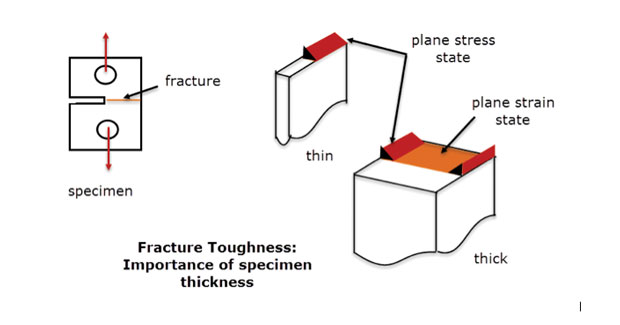5:ひびの靭性の標本;薄く、厚いセクション。図6は、接合継手を形成する複合構造に使用される他の成分を示す。 ここでは、断面は一定であり、十分に深いので、応力も深さとともに一定であると仮定することができます。 自由端面（at+z、-z）は、異なる局所応力状態（実際には平面応力）を有するが、この分析の目的は、中心線（z=0）上の正味断面応力をチェックすることである。
2D平面ひずみ解析メッシュは、図中の3D成分に分割されて示されています。 7. 区間カットは、駅z=0で定義されます。
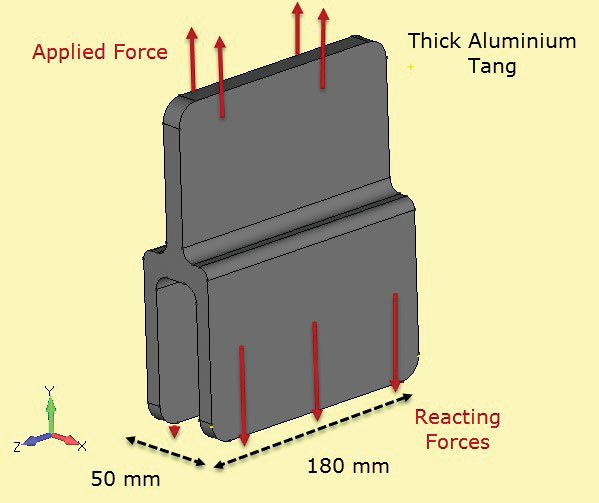図6：深断面アルミニウム唐。
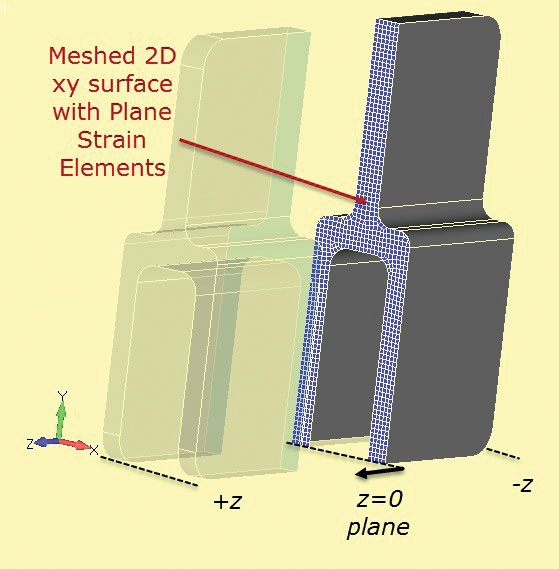7: 断面は、2D平面ひずみセクションを開発するために固体セクションを切断します。非常に微細な2D平面ひずみメッシュを使用することができ、完全な3Dモデルと比較して非常に迅速に実行されます。 2-1制約法は、以前と同様に使用されます。 負荷は慎重に考慮する必要があります。 平面ひずみセクションの”厚さ”は非常に任意であり、通常はデフォルトで1.0に設定されています。 部品の負荷が深さ（N/m、Lbf/inch等）による連続した負荷として計算されれば。）この値は、平面ひずみメッシュ上で直接使用することができます。 単一のタングなどのセクションを選択し、このセクションの公称応力または平均応力を完全なコンポーネントについて推定すると便利です。 これは、平面ひずみ解析における正気チェックとして使用することができます。 誤った読み込みは、おそらくこのメソッドのエラーの主な原因です。
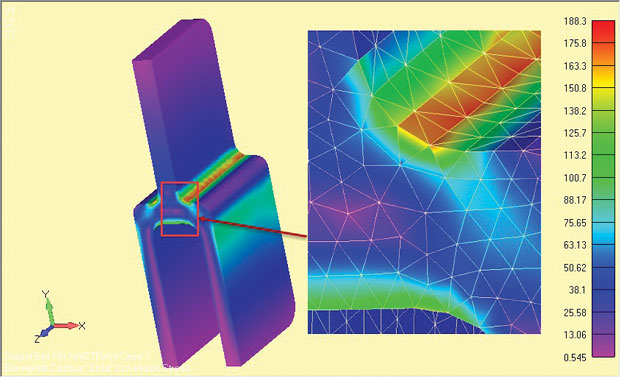
解析の結果を図に示す。 8および肩の肉付けのまわりで高い圧力の地域をはっきり示して下さい。 応力は、成分の中央の深さ領域(z=0)に対して有効です。
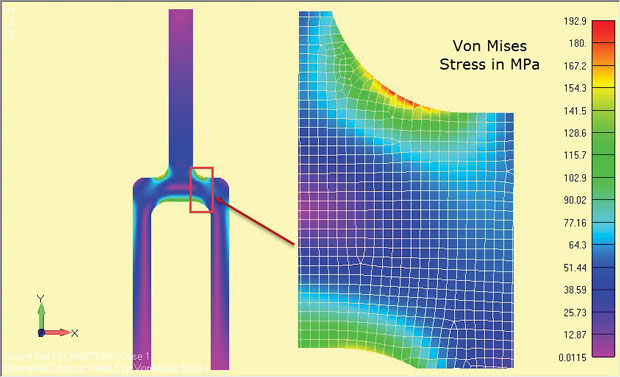8: 深唐成分の平面strain解析結果。使用される応力量は、使用されるソルバーによって異なります。 一部のソルバーは、z方向の応力を二次的なものとして無視し、平面内の応力を回復します。 主応力とvon Mises応力は、2次元の面内応力状態に関連します。 Ｚ方向応力が回復されるならば、ｘ−ｙ平面内の２Ｄ面内応力状態を識別することができるように、それは明確に識別されるべきである。
z方向の応力は正確には何を表していますか？ これは、ゼロz方向ひずみの強制のために発生する応力です。 応力はプリズム断面の自由端面が固定されているかのように作用する。 深い断面成分の中心平面では、これらはゼロz方向のひずみ状態を保持するために必要な相補的な応力になります。 実際には、自由表面面に向かって移動すると、z応力はゼロに低下し、平面応力分布になります（厚い破壊力学試験片に見られるように）。
加圧シリンダーのような多くの場合、端面はキャップされており、実際には軸力による軸方向の応力が発生します。 これは、平面strain解析における誘起軸応力とは異なる応力になります。 手の計算は軸圧力、または可能圧力容器のための補足のaxisymmetricモデルを計算するために必要である。
幾何学とメッシュ構造の容易さは、”what-if”研究やより正式な形状最適化研究に適しています。
比較のために、深い唐成分の半対称フル3D解析を行い、その結果を図に示す。 9. 上部の単一の唐の足を渡るわずかな圧力は両方の場合で同一である—これがあらゆる正気の点検の基礎であることを覚えなさい。
9:圧力の結果を示す深い唐の完全な3Dモデル。フルモデルでは、局所的な肩のストレスはわずかな割合で低くなっています。 これには3つの理由があります。 まず、比較的粗い3D tetメッシュは、非常に細かい2D平面ひずみローカルメッシュよりも劣っています。 3Dモデルの収束チェックは行われていません。
第二に、エンドフィレットによるz=0セクションと比較して、自由曲面（+z、-z）のジオメトリの小さな変化があります。 この場合、フィレットが肩の領域から離れているので、その効果は無視できる。 しかし、多くのコンポーネントでは、ローカルフィレットがあり、詳細が不足します。 これは、単純なxy平面からジオメトリを変化させます。 自由端面における局所応力変動は、完全な3Dモデルで推定またはチェックする必要がある場合があります。
最後に、+z、-zセクションでの固定z制約の平面ひずみの仮定は、有限の深さ成分については当てはまりません。 Z応力は、「実際の」自由面でゼロに拡散します。 この効果を図１ ０に示す。 図10に示すように、3Dモデルをそのまま使用し、また平面ひずみz応力のシミュレーションとしても使用する。
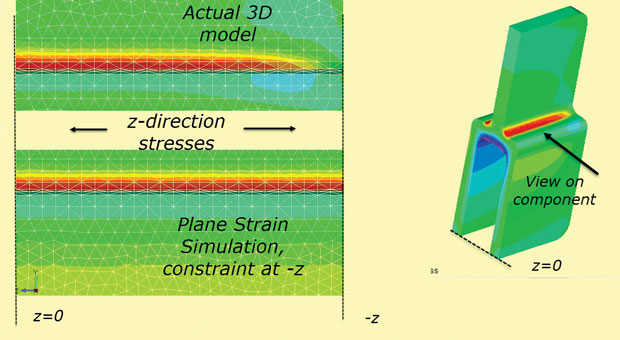図10:自由表面へのz応力の拡散。高速かつ効率的な
平面応力および平面ひずみ解析は、多くの場合、フルスケールの3Dモデルを補完することができる有用な2D方法です。 すべての特徴を表現できるわけではありませんが、いくつかの工夫をすれば、少なくとも重要な分野のストレスを推定することができます。 この方法を使用する動機は、簡単な2Dジオメトリとメッシュ構造で高速で効率的な解析を可能にすることです。