Sannsynligvis den mest brukte verdien i en jord rapport er jord bæreevne. Den åpenbare grunnen er at grunnleggende eksempler gitt i de fleste lærebøker nesten alltid bruker bæreevne til å beregne plandimensjonen til et fotfeste. På grunn av enkelhet og brukervennlighet er denne metoden fortsatt den grunnleggende jordparameteren for grunndesign. Men den enkelheten antar at fotfestet vil oppføre seg som en stiv kropp. Den spesielle antakelsen fungerer godt i praksis for små og enkle kolonne footings. Men for store og flere kolonnefundamenter, foretrekker de fleste ingeniører fleksibel analyse. Manuell beregning av fleksibel analyse kan være utfordrende, og i nesten alle tilfeller, programmer som STAAD, SAFE, GT STRUDL etc. brukes. Imidlertid ber disse dataprogrammene ofte om en inngang kalt «modulus of subgrade reaction». Mange ingeniører er ikke kjent med dette begrepet og prøver ofte å sammenligne det med bæreevne. Etter hvert som flere og flere ingeniører vil bruke programvare til å designe grunnlag, er det viktig for ingeniører å ha en grunnleggende forståelse av denne jordparameteren. Er det noen sammenheng mellom bæreevne og modul av undergradsreaksjon?
Modulus Av Subgrade Reaksjon (Ks)
denne termen måles og uttrykkes som lastintensitet per forskyvningsenhet. For det engelske enhetssystemet uttrykkes det ofte i kip / in2 / in; I SI-systemet uttrykkes det som kN / m2 / m. Noen uttrykker dette begrepet i kip / in3 (eller kN/m3) som kan være misvisende. Numerisk er kip / in3 riktig, men representerer ikke riktig den fysiske betydningen av den målte verdien og kan forveksles som en tetthetsenhet eller en volumetrisk måling.
matematisk uttrykkes undergradens reaksjonskoeffisient som:
Ks = p / s (Eqn 1)
hvor p = kontakttrykkintensitet og s = jordoppgjør
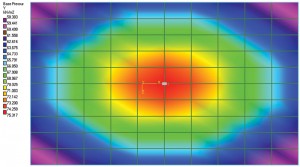
Figur 1a: Avbøyningsdiagram og jordtrykkkontur.
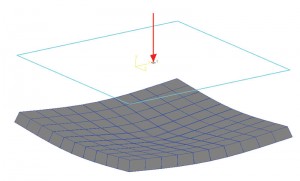
Figur 1b: jordtrykkkontur.
som Terzaghi nevnte, kan riktig estimering av kontakttrykk for et fleksibelt fundament være svært tungvint, så det antas At Ks forblir konstant for hele foten. Med andre ord vil forholdet mellom trykk og oppgjør på alle steder av fotfeste forbli konstant. Så forskyvningsdiagrammet til en fot med en last i midten vil ha en dishing effekt. Et punkt i midten av foten vil oppleve den høyeste forskyvningen. Forskyvning reduseres når den beveger seg bort fra sentrum. Figur 1a viser en enkel skive-på-klasse fundament. DET ble modellert OG analysert I STAAD Foundation som «Mat», som er et fleksibelt fundament; jorda ble definert ved hjelp av subgrade reaksjonskoeffisient. For denne øvelsen ble programvarens standardverdi for modulus av subgrade reaksjon brukt. Forskyvningsdiagrammet viser en dishing effekt som diskutert tidligere. Figur 1b viser jordtrykkkonturen. Det er også åpenbart at trykkintensiteten i midten er maksimal og reduseres når elementene (eller knutekoordinatene) beveger seg bort fra sentrum. Så det kan antas at forholdet mellom trykkintensitet og oppgjør er konstant.
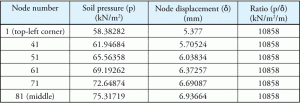
Tabell 1: Jordtrykk, knuteforskyvning og deres forhold.
Vurder noen av tallene fra samme eksempel. Jordtrykk, tilsvarende forskyvning og forholdet er oppført I Tabell 1. Punktene er representert på en diagonal for å illustrere variasjonen av trykk og forskyvning når punktene beveger seg bort fra midten til det fjerneste punktet i hjørnet av den rektangulære foten. Figur 2 viser punktene på matteplaten.
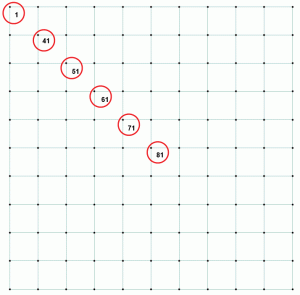
Figur 2: Utvalgte punkter for å sammenligne basetrykk, avbøyning og forhold.
dette er neppe en overraskelse som, per definisjon, modulus av subgrade reaksjon (Ks) er en konstant for hele foten og programmet brukt Ks som sin jord eiendom. Det er også viktig å merke seg at programvarens standard ks-verdi (10858 kN / m2/ m) var nøyaktig det samme som konstantforholdet beregnet i Tabell 1.
Basetrykket ble beregnet ut fra støttereaksjonen. Man kan tro at forholdet mellom støttereaksjon og tilsvarende forskyvning også vil være en konstant. Som vist i Tabell 2 er forholdene ikke konstante for alle verdier. Hvordan brukes ks-verdien inne i programmet og hvordan beregnes basetrykket?
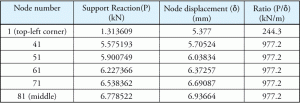
Tabell 2: støttereaksjon og forskyvning.
Sideelver
ofte blir det antatt å beregne hvor mye område av en plate som kan tilskrives en node eller med andre ord påvirkning av hver node på overflaten av en plate. Det avhenger av formen på platen. For en perfekt kvadratisk eller rektangulær plate vil hver node påvirke nøyaktig ¼ av platens overflateareal (Figur 3a). Men for en generalisert firkant vil den beste praksis være å beregne midten av platenes masse og deretter tegne linjer fra det midtpunktet til midtpunktene på hver side. I Figur 3b representerer det skyggelagte området påvirkningsflaten til den tilsvarende noden.
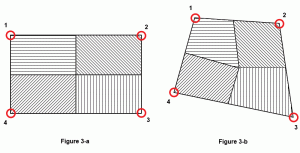
Figur 3: Node sideelvområde.
Fjærstøttekonstanten
beregningen av sideelver er nøkkelprosedyren som brukes internt av den kommersielle programvaren for å beregne den lineære fjærkonstanten. Programmet beregner først sideelven området for hver node av fotfeste og multipliserer deretter modulus av subgrade reaksjon ved den tilsvarende sideelven området for hver node for å få den lineære fjærkonstanten på hver node.
Kyi = Ks x Tai (Eqn 2)
hvor
Kyi er fjærkonstanten ved ith-noden
Tai er påvirkningsområdet til ith-noden
Ks er modulen for undergradsreaksjon
for en konkret fundamentanalyse må disse fjærene være definert som kompresjon-bare, som betong antas ikke Å Bære Noen Strekkraft. Basetrykket beregnes ved hver støtteknute ved å dele støttereaksjonen med det tilsvarende knuteområdet. Hvis Vi ser på eksemplet ovenfor, Har Node 1 et mye mindre biflodområde enn resten av noderne. Det kan også bemerkes at alle andre noder har samme bifloder. Dette forklarer Tabell 2, da det viser forholdet For Node 1 er forskjellig fra andre noder. Figur 4 viser sideflodområdet for forskjellige noder. Node 1 har et sideelvområde som er 25% Av Node 81. Tabell 3 er en utvidelse Av Tabell 1 og 2 og viser hvordan konstant forhold oppnås for alle noder.
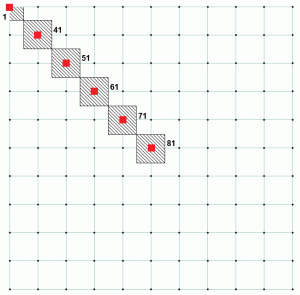
Figur 4: Sideelvområde for utvalgte noder.
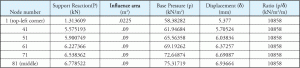
Tabell 3: Reaksjon, basetrykk, forskyvning, ks konstant.
Tillatte Oppgjør
Bæreevne er måling av jordtrykket en jord kan trygt bære. Med andre ord, bæreevne er trykket som jord kan tåle før det svikter. De to viktigste jordfeilkriteriene er:
- Skjærfeil
- maksimalt tillatt oppgjør
blant mange faktorer kan fundamentbredde (B) påvirke feilkriterier. Normalt, skjær svikt styrer for mindre stiftelser og oppgjør svikt styrer større stiftelser. Tabell 4 er et typisk eksempel som viser forholdet mellom ulike grunnstørrelser og feilkriterier.
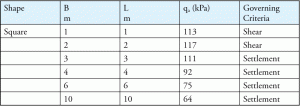
Tabell 4: Endelig tillatt bæreevne for tillatt oppgjør = 25 mm og en gitt innbyggingsdybde.
for å estimere utligningsfeil, antas en tillatt utligningsverdi (normalt 25 mm eller 1 tomme). Når jord legger seg mer enn den tillatte verdien, svikter jorda. Så, selv for en lagerkapasitetsberegning, brukes en tillatt jordoppgjør, og bygningsingeniører bør være oppmerksomme på den verdien mens de utformer en fot. Den tillatte jordoppgjørsverdien er vanligvis en integrert del av en jordrapport.
Hvorfor Bruke Modulus Av Subgrade Reaksjon
det ble tidligere uttalt at for å designe en fleksibel matte fundament, modulus av subgrade reaksjon brukes i stedet for bæreevne av jord. Men hvorfor? Svaret ligger i de underliggende forutsetningene for hvordan et fundament kan oppføre seg.
Stiftelser kan være stive eller fleksible. Bæreevne brukes til å designe stive fundamenter, men undergradereaksjon brukes til fleksible fundamenter. Selve antagelsen om et stivt fundament er at » fordelingen av undergradereaksjonen p over fundamentet av fundamentet må være plan, fordi et stivt fundament forblir plan når det legger seg.»Tenk på en enkelt støttet stråle lastet i midten, som vist i Figur 5a. ved statikk kan Vi få R1 = P / 2 Og R2 = P / 2. Hvis den samme strålen lastes eksentrisk, kan reaksjonen beregnes som vist i Figur 5b.
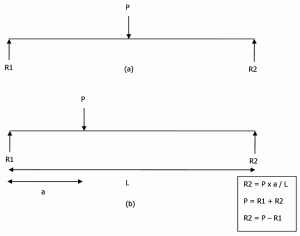
Figur 5: Reaksjoner for en enkelt støttet stråle.
det samme konseptet er utvidet for stiv fundamentdesign. Men i stedet for sluttstøttene støttes hele fundamentet. Det antas også at den relative stivheten til betongplaten er mye høyere enn jordens stivhet. Så antas platen å forbli plan selv etter påføring av belastning.
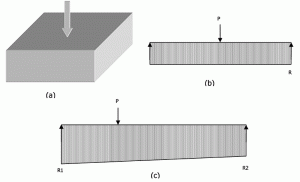
Figur 6: reaksjoner Undergradering for isolert fotfeste.
Figur 6a viser et fotfeste lastet i midten. Fra en stiv bredstråle analogi, P = r x L. På samme måte, for en eksentrisk lastet fot, vil reaksjonen variere lineært fra den ene enden til Den andre som vist i Figur 6c. Ligninger 3 og 4 kan løses for å finne endereaksjoner. Men ingen av ligningene inneholder modulus av subgrade reaksjon (Ks). Så, «fordelingen av undergradereaksjonen på bunnen av en stiv fot er uavhengig av graden av komprimerbarhet av undergraden» den hviler på. Som mange forfattere har konkludert, kan et stivt fundament sikkert utformes ved hjelp av bæreevne, da denne metoden i de fleste tilfeller gir mer konservative resultater.
P = 1/2l(R1 + R2) (Eqn 3)
P x a = 1/6B2R1 + 1/3b2r2 (Eqn 4)
men en mattefundament er ofte utformet som et fleksibelt fundament, da det kan være stort i størrelse og det kan være mange belastningspunkter og andre kompleksiteter, inkludert hull og bjelker. Utbredt tilgjengelighet AV FEA programvare bidrar til denne trenden. Men, i motsetning til stive fundament, kan et fleksibelt fundament ikke ha lineær undergradereaksjon. Snarere avhenger det av komprimerbarheten av fundamentet, så vel som strukturell stivhet. Et fleksibelt fundament blir utsatt for intern bøyning og relative forskyvninger mellom to platepunkter. Jo større strukturell stivhet, desto mindre er den relative forskyvningen. Forfatteren testet saken med svært høy stivhet av plateelementene, noe som resulterte i en nesten plan overflate etter påføring av lasten. Tilsvarende, jo større modulus av subgrade reaksjon, jo mindre trykkfordelingen. Med andre ord vil en høyere ks-verdi absorbere mer trykk ved belastningspunktet. Derfor brukes modulen av undergradereaksjon,som er funksjonen av jordoppgjør og det ytre trykket, for fleksibel grunndesign.
Korrelasjoner
det vanligste – og sannsynligvis det sikreste – svaret på spørsmålet om korrelasjon mellom bæreevne og modulus av subgrade reaksjon er at det ikke er noen korrelasjon. Men det skal være en, da begge er målinger av jordkapasitet, og noen av disse to parametrene kan brukes til å designe et vanlig fundament.
igjen er definisjonen Av Ks trykket per enhet oppgjør. Med andre ord, jordkapasitet til å motstå trykk for en gitt forskyvning. Fra tidligere diskusjoner er det også klart at selv lagerkapasitet har et tillatt oppgjør. Det er derfor fristende å konkludere med at modulus av subgrade reaksjon er bæreevne per enhet oppgjør.
denne konklusjonen er veldig lik ligningen presentert Av Bowles.
SI: Ks = 40 (SF)qa kN/m3 (Eqn 5)
FPS: Ks = 12 (SF)qa k / ft3 (Eqn 6)
HVOR SF = sikkerhetsfaktor og qa er tillatt bæreevne.
i Ligningene 5 og 6 blir den tillatte bæreevnen først konvertert til den ultimate bæreevnen ved å multiplisere med en sikkerhetsfaktor. Forfatteren antok en tomme eller 25 mm oppgjør. Den endelige ligningen blir deretter formulert dividere den endelige bæreevne ved antatt oppgjør.
den mer generiske formen av ligningen kan skrives som:
Ks = 
stress/forskyvning (Eqn 7)
hvor
I = sikkerhetsfaktor
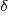er den tillatte jordoppgjøret
disse ligningene tyder tydelig på At Riktig Sikkerhetsfaktor Må Brukes, Og Ks-Verdien kan bedre sammenlignes med ultimate bæreevne i stedet for den tillatte Bæreevne. Sikkerhetsfaktoren kan variere avhengig av prosjekter og geotekniske ingeniører. Den andre viktige faktoren er den antatte tillatte oppgjøret for den beregnede lagerkapasiteten.
på Samme måte skal det bemerkes at basetrykkverdiene rapportert VED FEA-analyse ikke kan sammenlignes direkte med lagerkapasiteten. Maksimalt basetrykk skal multipliseres med sikkerhetsfaktoren og deretter sammenlignes med jordens tillatte bæreevne.
men de ovennevnte ligningene har begrensninger. De kan brukes på footings der utligningsfeil styrer, men kan ikke være relatert til footings der skjærfeil oppstår før den tillatte oppgjørsgrensen nås. Så, ingeniører må utvise forsiktighet før du bruker disse ligningene.
Konklusjon
korrelasjonen mellom bæreevne og modul av undergradsreaksjon er i beste fall et estimat. Den kan brukes til estimering, men En ks-verdi bestemt av en platebelastningstest bør alltid brukes hvis tilgjengelig eller bør bli forespurt når det er mulig. Den ovennevnte diskusjonen gir imidlertid innsikt i disse verdiene og hjelper ingeniører til å forstå den fysiske betydningen av modulus av subgrade reaksjon. Og, som alltid, bygningsingeniører bør konsultere en geoteknisk ingeniør profesjonell før sluttføre jord stivhet og bærende verdier.▪