Greedy algoritme met voorbeelden: Greedy Method & Approach

om de hebzuchtige benadering te begrijpen, moet u een praktische kennis hebben van recursie en context switching. Dit helpt u om te begrijpen hoe u de code te traceren. Je kunt het hebzuchtige paradigma definiëren in termen van je eigen noodzakelijke en voldoende uitspraken.

twee voorwaarden definiëren het hebzuchtige paradigma.

• elke stapsgewijze oplossing moet een probleem structureren in de richting van de best geaccepteerde oplossing.
• het is voldoende als de structurering van het probleem kan stoppen in een eindig aantal hebzuchtige stappen.

met de theorie voortgezet, laten we beschrijven de geschiedenis geassocieerd met de Greedy search benadering.

In deze hebzuchtige algoritme tutorial, zul je leren:

• geschiedenis van hebzuchtige algoritmen
• hebzuchtige strategieën en beslissingen
• kenmerken van de hebzuchtige benadering
• waarom de hebzuchtige benadering gebruiken?
• Hoe op te Lossen van de activiteit selectie probleem
• de Architectuur van de Hebzuchtige aanpak
• Nadelen van Greedy Algoritmen

Geschiedenis van Greedy Algoritmen

Hier is een belangrijke mijlpaal van greedy algoritmen:

• Greedy algoritmen werden ontworpen voor vele grafiek lopen algoritmen in de jaren 1950.
• Esdger Djikstra geconceptualiseerd het algoritme voor het genereren van een minimale spanning bomen. Hij wilde de trajecten binnen de Nederlandse hoofdstad Amsterdam inkorten.
• in hetzelfde decennium bereikten Prim en Kruskal optimalisatiestrategieën die waren gebaseerd op het minimaliseren van de kosten van wegen langs gewogen routes. In de jaren ‘ 70 stelden Amerikaanse onderzoekers, Cormen, Rivest en Stein een recursieve substructuur van hebzuchtige oplossingen voor in hun boek classical introduction to algorithms.
• het hebzuchtige zoekparadigma werd in 2005 geregistreerd als een ander type optimalisatiestrategie in de NIST-records.
• tot op heden gebruiken protocollen die het web draaien, zoals de open-shortest-path-first (OSPF) en vele andere netwerkpakketschakelprotocollen de hebzuchtige strategie om de tijd die op een netwerk wordt doorgebracht te minimaliseren.

hebzuchtige strategieën en beslissingen

de logica in zijn eenvoudigste vorm werd teruggebracht tot “hebzuchtig” of “niet hebzuchtig”. Deze verklaringen werden bepaald door de aanpak die werd genomen om vooruit te gaan in elke algoritme fase.

het algoritme van Djikstra gebruikte bijvoorbeeld een stapsgewijze hebzuchtige strategie om hosts op het Internet te identificeren door een kostenfunctie te berekenen. De waarde die door de kostenfunctie wordt geretourneerd, bepaalt of het volgende pad “hebzuchtig” of “niet-hebzuchtig”is.

kortom, een algoritme houdt op hebzuchtig te zijn als het op enig moment een stap zet die niet lokaal hebzuchtig is. De hebzuchtige problemen stoppen zonder verdere reikwijdte van hebzucht.

kenmerken van de hebzuchtige benadering

de belangrijkste kenmerken van een algoritme van de hebzuchtige methode zijn::

• er is een geordende lijst van middelen, met kosten of waarde toeschrijvingen. Deze kwantificeren beperkingen op een systeem.
• u neemt de maximale hoeveelheid hulpbronnen in de tijd dat een beperking van toepassing is.
• bij een probleem met de planning van activiteiten zijn de kosten van middelen uitgedrukt in uren en moeten de activiteiten in volgorde van volgorde worden uitgevoerd.

Waarom gebruik maken van de hebzuchtige aanpak?

hier zijn de redenen voor het gebruik van de hebzuchtige benadering:

• de hebzuchtige aanpak heeft een paar afwegingen, die het geschikt kunnen maken voor optimalisatie.
• een belangrijke reden is om onmiddellijk tot de meest haalbare oplossing te komen. In het activiteitenselectieprobleem (hieronder uitgelegd), als er meer activiteiten kunnen worden gedaan voordat de huidige activiteit wordt beëindigd, kunnen deze activiteiten binnen dezelfde tijd worden uitgevoerd.
• een andere reden is om een probleem recursief te verdelen op basis van een voorwaarde, zonder dat alle oplossingen moeten worden gecombineerd.
• bij het probleem van de activiteitsselectie wordt de stap” recursieve deling ” bereikt door een lijst van items slechts één keer te scannen en bepaalde activiteiten te overwegen.

het probleem van de selectie van activiteiten oplossen

in het voorbeeld van de planning van activiteiten is er een” start “- en” finish ” – tijd voor elke activiteit. Elke activiteit wordt geïndexeerd met een nummer ter referentie. Er zijn twee categorieën activiteiten.

1. beschouwde activiteit :is de activiteit, die de referentie is van waaruit het vermogen om meer dan één resterende activiteit uit te voeren wordt geanalyseerd.
2. overige activiteiten: activiteiten op een of meer indexen voorafgaand aan de betrokken activiteit.

de totale duur geeft de kosten van de uitvoering van de activiteit weer. Dat wil zeggen (finish – start) geeft ons de duur als de kosten van een activiteit.

u leert dat de hebzuchtige omvang is het aantal resterende activiteiten die u kunt uitvoeren in de tijd van een overwogen activiteit.

architectuur van de hebzuchtige benadering

stap 1)

Scan de lijst van activiteitskosten, te beginnen met index 0 als de beschouwde Index.

stap 2)

wanneer meer activiteiten kunnen worden voltooid tegen de tijd dat de overwogen activiteit is voltooid, start u met zoeken naar een of meer resterende activiteiten.

stap 3)

als er geen resterende activiteiten meer zijn, wordt de huidige resterende activiteit de volgende beschouwde activiteit. Herhaal stap 1 en stap 2, met de nieuwe overwogen activiteit. Als er geen activiteiten meer over zijn, ga dan naar stap 4.

stap 4)

Geef de Unie van onderzochte indices weer. Dit zijn de activiteitsindices die zullen worden gebruikt om de doorvoer te maximaliseren.

Code-uitleg

#include<iostream>#include<stdio.h>#include<stdlib.h>#define MAX_ACTIVITIES 12

verklaring van de code:

1. opgenomen headerbestanden / klassen
2. een max. aantal door de gebruiker verstrekte activiteiten.

using namespace std;class TIME{ public: int hours; public: TIME() { hours = 0; }};

verklaring van de code:

1. de naamruimte voor streamingbewerkingen.
2. een klasse-definitie voor tijd
3. een uurstempel.
4. a TIME default constructor
5. de urenvariabele.

class Activity{ public: int index; TIME start; TIME finish; public: Activity() { start = finish = TIME(); }};

Uitleg van de code:

1. Een klasse definitie van activiteit
2. Tijdstempels het definiëren van een duur
3. Alle timestamps worden geïnitialiseerd op 0 in de default constructor

class Scheduler{ public: int considered_index,init_index; Activity *current_activities = new Activity; Activity *scheduled;

Uitleg van de code:

1. Deel 1 van de planner class-definitie.
2. beschouwde Index is het startpunt voor het scannen van de array.
3. de initialisatie-index wordt gebruikt om willekeurige tijdstempels toe te wijzen.
4. een reeks activiteitenobjecten wordt dynamisch toegewezen met behulp van de nieuwe operator.
5. de geplande aanwijzer definieert de huidige basislocatie voor hebzucht.

Scheduler(){ considered_index = 0; scheduled = NULL;......

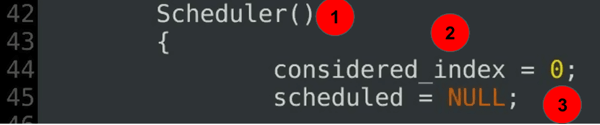
verklaring van de code:

1. de scheduler constructor-deel 2 van de scheduler klasse definitie.
2. de beschouwde index bepaalt de huidige start van de huidige scan.
3. de huidige gulzige omvang is in het begin niet gedefinieerd.

for(init_index = 0; init_index < MAX_ACTIVITIES; init_index++) { current_activities.start.hours = rand() % 12; current_activities.finish.hours = current_activities.start.hours + (rand() % 2); printf("\nSTART:%d END %d\n", current_activities.start.hours ,current_activities.finish.hours); }……

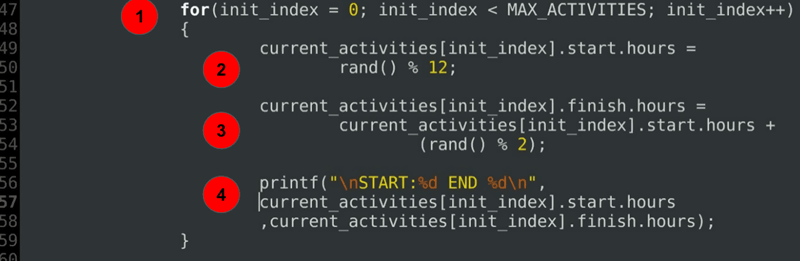
verklaring van de code:

1. A Voor loop om begin-en einduren van elk van de momenteel geplande activiteiten te initialiseren.
2. starttijd initialisatie.
3. initialisatie van de eindtijd altijd na of precies op het beginuur.
4. een debug-instructie om de toegewezen duur af te drukken.

public: Activity * activity_select(int);};

verklaring van de code:

1. Deel 4 – Het Laatste deel van de scheduler klasse definitie.
2. Activity select functie neemt een startpunt-index als basis en verdeelt de hebzuchtige quest in hebzuchtige subproblemen.

Activity * Scheduler :: activity_select(int considered_index){ this->considered_index = considered_index; int greedy_extent = this->considered_index + 1;…… 

1. met behulp van de scope resolution operator (::) wordt de functiedefinitie gegeven.
2. de beschouwde Index is de index genoemd naar waarde. De greedy_extent is de geïnitialiseerde slechts een index na de beschouwde Index.

Activity * Scheduler :: activity_select(int considered_index){ while( (greedy_extent < MAX_ACTIVITIES ) && ((this->current_activities).start.hours < (this->current_activities).finish.hours )) { printf("\nSchedule start:%d \nfinish%d\n activity:%d\n", (this->current_activities).start.hours, (this->current_activities).finish.hours, greedy_extent + 1); greedy_extent++; }…...

verklaring van de code:

1. de kernlogica – de hebzuchtige omvang is beperkt tot het aantal activiteiten.
2. de beginuren van de huidige activiteit worden als planningsbaar gecontroleerd voordat de beschouwde activiteit (gegeven door beschouwde index) zou eindigen.
3. zolang dit mogelijk is, wordt een optionele debug-instructie afgedrukt.
4. doorgaan naar de volgende index op de activiteitenserie

...if ( greedy_extent <= MAX_ACTIVITIES ) { return activity_select(greedy_extent); } else { return NULL; }}

verklaring van de code:

1. de voorwaardelijke controles indien alle activiteiten in aanmerking zijn genomen.
2. indien niet, kunt u uw greedy opnieuw opstarten met de beschouwde Index als het huidige punt. Dit is een recursieve stap die gretig verdeelt de probleemstelling.
3. zo ja, keert het terug naar de beller zonder ruimte voor het uitbreiden van hebzucht.

int main(){ Scheduler *activity_sched = new Scheduler(); activity_sched->scheduled = activity_sched->activity_select( activity_sched->considered_index); return 0;}

verklaring van de code:

1. de belangrijkste functie die wordt gebruikt om de scheduler aan te roepen.
2. er wordt een nieuwe planner geïnstalleerd.
3. de activity select functie, die een pointer van type activiteit geeft, komt terug naar de beller nadat de hebzuchtige zoektocht voorbij is.

Output:

START:7 END 7START:9 END 10START:5 END 6START:10 END 10START:9 END 10Schedule start:5 finish6 activity:3Schedule start:9 finish10 activity:5

nadelen van hebzuchtige algoritmen

het is niet geschikt voor hebzuchtige problemen waar een oplossing nodig is voor elk subprobleem zoals sorteren.

in dergelijke hebzuchtige algoritmepraktijkproblemen kan de hebzuchtige methode verkeerd zijn; in het ergste geval zelfs leiden tot een niet-optimale oplossing.

het nadeel van hebzuchtige algoritmen is het niet weten wat er voor de huidige hebzuchtige staat ligt.

Hieronder is een afbeelding van het nadeel van de hebzuchtige methode:

in de greedy scan hier weergegeven als een boom (hogere waarde hogere hebzucht), een algoritme staat op waarde: 40, is waarschijnlijk 29 nemen als de volgende waarde. Verder eindigt zijn zoektocht om 12 uur. Dit komt neer op een waarde van 41.

echter, als het algoritme een suboptimaal pad heeft gekozen of een veroveringsstrategie heeft aangenomen. dan 25 zou worden gevolgd door 40, en de totale kosten verbetering zou 65, die wordt gewaardeerd 24 punten hoger als een suboptimale beslissing.

voorbeelden van hebzuchtige algoritmen

de meeste netwerkalgoritmen gebruiken de hebzuchtige benadering. Hier is een lijst van enkele hebzuchtige algoritme voorbeelden:

• Prim ‘ s Minimal Spanning Tree Algoritme
• Travelling Salesman Problem
• Grafiek – Kaart Kleuren
• Kruskal de Minimal Spanning Tree Algoritme
• Dijkstra de Minimal Spanning Tree Algoritme
• Grafiek – Vertex Cover
• Knapzak Probleem
• Job Scheduling Probleem

Samenvatting:

samen Te vatten, het artikel gedefinieerd de hebzuchtige paradigma, liet zien hoe gulzige optimalisatie en recursie, kan u helpen het verkrijgen van de beste oplossing tot een punt. Het hebzuchtige algoritme wordt op grote schaal gebruikt voor het oplossen van problemen in vele talen als hebzuchtige algoritme Python, C, C#, PHP, Java, enz. De activiteit selectie van hebzuchtige algoritme voorbeeld werd beschreven als een strategisch probleem dat maximale doorvoer met behulp van de hebzuchtige aanpak kon bereiken. Uiteindelijk werden de nadelen van het gebruik van de hebzuchtige aanpak uitgelegd.