El campo eléctrico E siempre se puede expresar como el gradiente de una función de potencial escalar
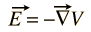
No existe un potencial escalar general para el campo magnético B, pero puede expresarse como el rizo de una función vectorial
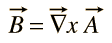
A esta función A se le da el nombre de «potencial vectorial», pero no está directamente asociada con el trabajo de la forma en que lo está el potencial escalar.
El potencial vectorial se define como consistente con la Ley de Amperios y puede expresarse en términos de corriente i o densidad de corriente j (las fuentes de campo magnético). En varios textos esta definición toma las formas
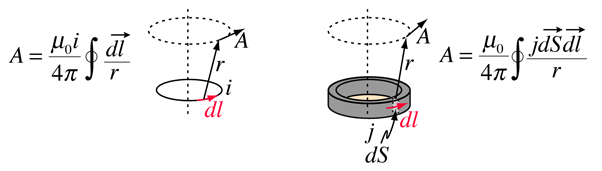
Una de las razones del potencial vectorial es que puede ser más fácil calcular el potencial vectorial que calcular el campo magnético directamente a partir de una geometría de corriente de origen dada. Su aplicación más común es la teoría de antenas y la descripción de ondas electromagnéticas.
Dado que el campo magnético B se define como el rizo de A, y la identidad por vector el rizo de un gradiente es idéntico a cero, entonces cualquier función arbitraria que pueda expresarse como el gradiente de una función escalar puede agregarse a A sin cambiar el valor de B obtenido de ella. Es decir, Un ‘puede sustituirse libremente por un donde
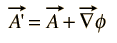
Tales transformaciones se llaman transformaciones de gauge, y ha habido una serie de» gauge » que se han utilizado para sacar ventaja de tipos específicos de cálculos en teoría electromagnética.