Algoritmo ganancioso com exemplos: abordagem & método ganancioso

para compreender a abordagem gananciosa, terá de ter um conhecimento funcional da recursão e mudança de contexto. Isso ajuda você a entender como rastrear o código. Você pode definir o paradigma ganancioso em termos de suas próprias declarações necessárias e suficientes.

duas Condições definem o paradigma ganancioso.

• cada solução gradual deve estruturar um problema para a sua solução mais bem aceite.
• é suficiente se a estruturação do problema pode parar em um número finito de passos gananciosos.

com a teorização continuou, vamos descrever a história associada com a busca gananciosa abordagem.

neste algoritmo Ganancioso tutorial, você vai aprender:

• História dos Gananciosos Algoritmos
• Gananciosos Estratégias e Decisões
• Características da Abordagem Gananciosa
• Por que usar a Abordagem Gananciosa?
• Como Resolver a atividade de seleção de problema
• Arquitetura da abordagem Gananciosa
• Desvantagens dos Algoritmos Greedy

Histórico dos Gananciosos Algoritmos

Aqui é um marco importante de algoritmos greedy:

• Ganancioso algoritmos foram conceituada por muitos gráfico pé algoritmos na década de 1950.
• Esdger Djikstra conceituou o algoritmo para gerar o mínimo de árvores de expansão. Ele pretendia encurtar a extensão das rotas dentro da capital holandesa, Amsterdã. Na mesma década, Prim e Kruskal alcançaram estratégias de otimização que foram baseadas na minimização dos custos do caminho ao longo de rotas pesadas.
• In the ’70s, American researchers, Cormen, Rivest, and Stein proposed a recursive substructuring of greedy solutions in their classical introduction to algorithms book.
• The Greedy search paradigm was registered as a different type of optimization strategy in the NIST records in 2005.
• Till date, protocolos que executam a web, como o Open-shortest-path-first (OSPF) e muitos outros protocolos de comutação de pacotes de rede usam a estratégia gananciosa para minimizar o tempo gasto em uma rede.

estratégias e decisões gananciosas

a lógica na sua forma mais fácil foi resumida em “ganancioso”ou” não ganancioso”. Estas afirmações foram definidas pela abordagem tomada para avançar em cada etapa do algoritmo.

por exemplo, o algoritmo de Djikstra utilizou uma estratégia ambiciosa identificando hosts na Internet calculando uma função de custo. O valor devolvido pela função de custo determinado se o próximo caminho é “ganancioso” ou “não-ganancioso”.

em resumo, um algoritmo deixa de ser ganancioso se, em qualquer fase, tomar um passo que não é localmente ganancioso. Os problemas gananciosos param sem mais ambição.

características da abordagem gananciosa

as características importantes de um algoritmo de método ganancioso são::

• há uma lista ordenada de recursos, com custos ou imputações de valor. Estes condicionalismos de quantificação de um sistema.
• você terá a quantidade máxima de recursos no tempo em que uma restrição se aplica.Por exemplo, em um problema de agendamento de atividade, os custos de recursos são em horas, e as atividades precisam ser realizadas em ordem série.

porquê usar a abordagem gananciosa?

Aqui estão as razões para usar a abordagem gananciosa:

• a abordagem gananciosa tem alguns tradeoffs, o que pode torná-lo adequado para otimização.
• uma razão proeminente é conseguir a solução mais viável imediatamente. No problema de seleção de atividades (explicado abaixo), se mais atividades podem ser realizadas antes de terminar a atividade atual, essas atividades podem ser realizadas ao mesmo tempo.
• outra razão é dividir um problema recursivamente baseado em uma condição, sem necessidade de combinar todas as soluções.
• no problema de seleção da atividade, o passo” divisão recursiva ” é alcançado digitalizando uma lista de itens apenas uma vez e considerando certas atividades.

como resolver o problema de seleção de atividade

no exemplo de agendamento de atividade, há um tempo de” início” e ” fim ” para cada atividade. Cada actividade é indexada por um número de referência. Existem duas categorias de atividades.

1. actividade considerada: é a actividade, que é a referência a partir da qual se analisa a capacidade de fazer mais do que uma actividade restante.
2. actividades restantes: actividades com um ou mais índices à frente da actividade considerada.

a duração total indica o custo da realização da actividade. Isto é (fim – início) nos dá a duração como o custo de uma atividade.

irá aprender que a extensão gananciosa é o número de actividades restantes que pode realizar no momento de uma actividade considerada.

Architecture of the Greedy approach

STEP 1)

Scan the list of activity costs, starting with index 0 as the considered Index.

Passo 2)

Quando Mais atividades podem ser concluídas até o momento, a atividade considerada termina, começar a procurar por uma ou mais atividades restantes.

Passo 3)

se não houver mais actividades remanescentes, a actividade remanescente actual torna-se a actividade seguinte considerada. Repetir o Passo 1 e o PASSO 2, com a nova actividade considerada. Se não restarem actividades, passar ao passo 4.

Passo 4)

devolver a união dos índices considerados. Estes são os índices de atividade que serão usados para maximizar o rendimento.

Explicação do Código

#include<iostream>#include<stdio.h>#include<stdlib.h>#define MAX_ACTIVITIES 12

Explicação do código:

1. arquivos de cabeçalho Incluído/classes
2. Um número máximo de atividades fornecidas pelo usuário.

using namespace std;class TIME{ public: int hours; public: TIME() { hours = 0; }};

explicação de código:

1. o espaço de nomes para as operações de streaming.
2. uma definição de classe para o tempo
3. uma hora de intervalo.
4. um construtor por defeito de tempo
5. a variável horas.

class Activity{ public: int index; TIME start; TIME finish; public: Activity() { start = finish = TIME(); }};

Explicação do código:

1. Uma definição de classe de atividade
2. Carimbos de data / hora de definir uma duração
3. Todos os carimbos de data / hora são inicializados a 0 no construtor padrão

class Scheduler{ public: int considered_index,init_index; Activity *current_activities = new Activity; Activity *scheduled;

Explicação do código:

1. Parte 1 do agendador de definição de classe.
2. o índice considerado é o ponto de partida para a digitalização da matriz.
3. o índice de inicialização é usado para atribuir datas aleatórias.
4. um conjunto de objetos de atividade é dinamicamente alocado usando o novo operador.
5. o ponteiro programado define a base atual para a ganância.

Scheduler(){ considered_index = 0; scheduled = NULL;......

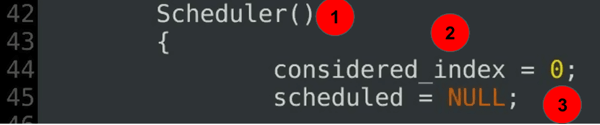
explicação de código:

1. o construtor do scheduler-parte 2 da definição da classe scheduler.
2. o índice considerado define o início actual da digitalização actual.
3. a extensão gananciosa actual não é definida no início.

for(init_index = 0; init_index < MAX_ACTIVITIES; init_index++) { current_activities.start.hours = rand() % 12; current_activities.finish.hours = current_activities.start.hours + (rand() % 2); printf("\nSTART:%d END %d\n", current_activities.start.hours ,current_activities.finish.hours); }……

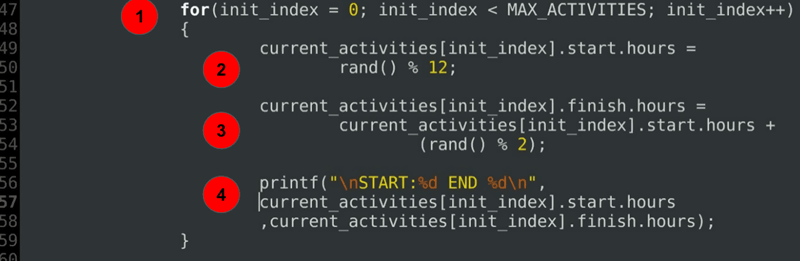
explicação de código:

1. a for loop to initialize start hours and end hours of each of the activities currently scheduled.
2. inicialização da hora de início.
3. inicialização da hora final sempre após ou exatamente na hora de início.
4. uma declaração de depuração para imprimir as Durações atribuídas.

public: Activity * activity_select(int);};

explicação de código:

1. Parte 4-a última parte da definição de classe scheduler.
2. a função de selecção da actividade toma um índice de ponto de partida como base e divide a busca gananciosa em subproblemas gananciosos.

Activity * Scheduler :: activity_select(int considered_index){ this->considered_index = considered_index; int greedy_extent = this->considered_index + 1;…… 

1. usando o operador de resolução de escopo (::), a definição da função é fornecida.
2. o índice considerado é o índice chamado por valor. O greedy_extent é o inicializado apenas um índice após o índice considerado.

Activity * Scheduler :: activity_select(int considered_index){ while( (greedy_extent < MAX_ACTIVITIES ) && ((this->current_activities).start.hours < (this->current_activities).finish.hours )) { printf("\nSchedule start:%d \nfinish%d\n activity:%d\n", (this->current_activities).start.hours, (this->current_activities).finish.hours, greedy_extent + 1); greedy_extent++; }…...

explicação de código:

1. a lógica central – a extensão gananciosa é limitada ao número de atividades.
2. as horas de início da actividade actual são verificadas como escalonáveis antes de a actividade considerada (dada pelo índice considerado) terminar.
3. enquanto isso for possível, uma declaração de depuração opcional é impressa.
4. avançar para o próximo índice sobre a atividade de matriz

...if ( greedy_extent <= MAX_ACTIVITIES ) { return activity_select(greedy_extent); } else { return NULL; }}

Explicação do código:

1. O condicional verifica se todas as atividades que foram cobertas. Se não, pode reiniciar o seu ganancioso com o índice considerado como o ponto actual. Este é um passo recursivo que avidamente divide a afirmação do problema.
2. se sim, retorna para o ouvinte sem margem para aumentar a ganância.

int main(){ Scheduler *activity_sched = new Scheduler(); activity_sched->scheduled = activity_sched->activity_select( activity_sched->considered_index); return 0;}

explicação de código:

1. a função principal usada para invocar o scheduler.
2. um novo Scheduler está instanciado.
3. a função de selecção da actividade, que devolve um indicador de actividade do tipo, volta para a pessoa que ligou depois de a busca gananciosa ter terminado.

saída:

START:7 END 7START:9 END 10START:5 END 6START:10 END 10START:9 END 10Schedule start:5 finish6 activity:3Schedule start:9 finish10 activity:5

desvantagens de algoritmos gananciosos

não é adequado para problemas gananciosos onde uma solução é necessária para cada subproblema como a ordenação.

in such Greedy algorithm practice problems, the Greedy method can be wrong; in the worst case even lead to a non-optimal solution.

portanto, a desvantagem dos algoritmos gananciosos é não saber o que está à frente do estado ganancioso atual.

abaixo está uma representação da desvantagem do método ganancioso:

no scan ganancioso mostrado aqui como uma árvore (maior valor ganância), um estado algoritmo no valor: 40, é provável que tome 29 como o próximo valor. Além disso, a sua busca termina aos 12 anos. Isto equivale a um valor de 41.

no entanto, se o algoritmo tomou um caminho sub-ideal ou adotou uma estratégia de conquista. em seguida, 25 seriam seguidos de 40, e a melhoria global dos custos seria de 65, que é avaliada 24 pontos mais alta como uma decisão suboptima.

Examples of Greedy Algorithms

Most networking algorithms use the greedy approach. Aqui está uma lista de alguns exemplos gananciosos de algoritmo:

• Prim Mínimos para o Algoritmo de Árvore abrangente
• Problema do Caixeiro viajante
• Gráfico de Mapa de Colorir
• Kruskal Mínimos para o Algoritmo de Árvore abrangente
• Dijkstra Mínimo Algoritmo de Árvore abrangente
• Gráfico – Cobertura de Vértices
• Mochila Problema
• Problema de Agendamento de Trabalho

Resumo:

Para resumir, o artigo definido o ganancioso paradigma, mostrou quão ganancioso otimização e a recursividade, pode ajudá-lo a obter a melhor solução, até um certo ponto. O algoritmo Greedy é amplamente levado em aplicação para a resolução de problemas em muitas linguagens como algoritmo Greedy Python, C, C#, PHP, Java, etc. A seleção de atividade do algoritmo ganancioso exemplo foi descrito como um problema estratégico que poderia alcançar o máximo de rendimento usando a abordagem gananciosa. No final, os deméritos do uso da abordagem gananciosa foram explicados.