CONDUTIVIDADE TÉRMICA

condutividade Térmica dos sólidos é de uma natureza diferente, dependendo se ou não eles são condutores. Em dielétricos sem cargas elétricas gratuitas, a energia térmica é transferida por fonons. As vibrações coletivas dos átomos na rede de cristais tomam a forma de ondas de deslocamento, cuja interferência gera pacotes de ondas, ou seja, fonões. As ondas de deslocamento trazem flutuações de densidade que podem ser manifestadas como uma variação do índice refrativo. Se as ondas passam por uma região na qual o índice de refração difere do valor volumétrico médio, as ondas de deslocamento subsequentes que transportam a energia do movimento térmico serão dispersas.A dispersão é a mais forte, quanto mais o desvio máximo dos átomos em relação às suas posições médias na estrutura, ou seja, quanto maior for o desvio máximo dos átomos em relação às suas posições médias na estrutura. Isto explica o fato experimentalmente estabelecido de que a condutividade térmica de dielétricos cristalinos diminui a temperaturas bastante altas: λ1/T (Figura 1).

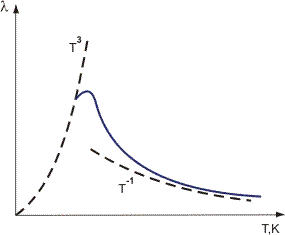
Figura 1. Variation of thermal conductivity of crystal dielectrics with temperature.

Debye deu uma visão sobre um caráter de variação λ (T) em baixo T dentro do quadro de conceitos de mecânica quântica. He elabored a dipole theory of dielectrics based on the concept of a molecule as a rigid dipole. Neste modelo Debye introduziu o conceito da chamada temperatura de Debye θD proporcional à frequência máxima das vibrações atômicas em um sólido. Para a maioria das substâncias, θD é inferior ou próximo da temperatura ambiente (uma excepção é o diamante para o qual θD = 1850 K e berrylium para o qual θD = 1160K).

Em teoria quântica de sólidos, a cristalina, é considerada como um volume preenchido com o phonon do gás, para que a dedução da mais simples a teoria cinética é aplicada

onde c é a capacidade térmica de um dielétrico que coincide com a de phonon do gás, v a velocidade média de phonons aproximadamente igual à velocidade do som,o caminho livre médio de phonons. A existência de um certo valor finito de é o resultado da dispersão de fonons em fonons, em defeitos da rede de cristal e, em particular, em limites de grãos sobre toda a amostra. A dependência da temperatura λ(T) é determinada pela dee c em relação à temperatura.

a altas temperaturas substancialmente excedendo a temperatura de Debye θD, o mecanismo básico que limita é uma dispersão fonon-fononante devido a uma harmonicidade de vibrações atômicas em um cristal. O phonon-phonon mecanismo de resistência térmica ((1/λ) é conhecido como o coeficiente de resistência térmica) só é viável devido a uma transição, resultando em retardo do phonon fluxo e apreciável mudança de quase-dinâmica. Quanto maior o T, maior a probabilidade da transição com diminuindo:(1/T). Uma vez que a T > θD a capacidade térmica c apenas aumenta ligeiramente com a temperatura, portanto, λ 1 / T.

A temperaturas inferiores a temperatura de Debye, T<<θD, o comprimento do caminho livre médiodeterminado pelo phonon-phonon dispersão aumenta drasticamente,expθD/T e, como regra, é limitado ao tamanho de um cristal R. de Acordo com a lei de Debye capacidade térmica c nesta faixa de temperatura varia como c(T/θD)3. Consequentemente, em t → 0 o coeficiente de condutividade térmica λ deve diminuir em proporção a T3. A temperatura para a qual a condutividade térmica tem um pico é determinada a partir de≈ R, que normalmente corresponde a t ≤ 0,05 θD.

this theory also accounts for the behavior of the coefficient of thermal conductivity for amorphous substances having no long-range order, i.e., the size of their “crystals” is of the order of atomic sizes. Em virtude disso, a dispersão nos “limites” destas substâncias deve prevalecer EM T e≈ const. O coeficiente de condutividade térmica das substâncias amorficas λ T3 a baixas temperaturas e deve crescer ligeiramente, em proporção à capacidade térmica, a temperaturas moderadas e elevadas, T > θD.

tudo isso fornece uma explicação qualitativa da dependência λ(T) em dielétricos cristalinos reais, mas não leva em conta desvios da estrutura constante devido a impurezas atômicas de outros elementos e seus próprios isótopos. A uma temperatura elevada, a resistência oferecida pelas impurezas ao transporte de calor é independente da temperatura. Isto torna possível estimar o grau de pureza cristalina a partir da variação de sua condutividade térmica com a temperatura. O mesmo fato nos permite determinar a distribuição entre a substância vítrea e cristalina no mineral natural se o vidro é considerado como uma impureza em um cristal.

a condutividade térmica nos metais depende do movimento e interação dos portadores da corrente, isto é, elétrons de condução. Geralmente, o coeficiente de condutividade térmica λ de um metal é igual à soma de malha (phonon) λph, e elétron λe componentes, λ = λe + λph; em temperaturas normais, como uma regra, λe >>λph.

Se aplicarmos uma simples teoria cinética dos gases para o fluxo de elétrons livres, e suponha que o comprimento de seu caminho livre não depende da velocidade e, em seguida, a teoria implica que

onde e é o elétron de carga, K Boltzrnann constante, e σ a condutividade elétrica. Um rigoroso da mecânica quântica teoria oferece uma relação semelhante,

Em ambas as fórmulas a relação entre o elétron parte do coeficiente de condutividade térmica λ a condutividade elétrica σ, em uma ampla faixa de temperatura, parece estar em proporção com a temperatura de acordo com o Wiedemann-Franz lei, λ/σ = L, onde L é o número de Lorentz. Esta lei é usada para calcular λe a partir da condutividade elétrica medida. No entanto, ele é violado a temperaturas abaixo de θD quando uma interação elétron-fonão prevalece (σ cresce com T decrescente como T−5 enquanto le varia mais ligeiramente como T−2).

os resultados experimentais evidenciam que, como regra, a condutividade térmica dos metais a altas temperaturas é uma função ligeiramente decrescente da temperatura. Mas há muitas excepções. Assim, a condutividade térmica do ferro diminui fortemente com a temperatura, enquanto o tântalo e nióbio apresentam um coeficiente de temperatura positivo.

De interesse são as tentativas para comparar os coeficientes de condutividade térmica para diferentes substâncias para uma única temperatura característica, por exemplo, para o ponto de fusão Tm de sólidos. Assim, o processamento estatístico de dados experimentais realizadas por Missenard tem mostrado que a condutividade térmica de metais em fusão ponto de λ(T = Tm) = λm é proporcional a λe condutividade térmica de dielectrical cristais em T = Tm está em proporção, onde m é a massa molecular, N o número de átomos na fórmula química, ρ a densidade e o ponto de fusão Tm é em Kelvins.

o transporte de calor em semicondutores é mais complexo do que em dielétricos e metais, porque os componentes fonon e elétrons são igualmente essenciais para eles. Outra razão para a complexidade é o efeito considerável das impurezas, difusão bipolar, e outros poucos fatores estudados na transferência de calor.

O efeito da pressão sobre a condutividade térmica de sólidos pode ser assumida, com uma boa precisão, para ser linear, λ para muitos metais, crescendo com p.

Para o efeito da porosidade na condutividade térmica de sólidos consulte Meio Poroso.