I have started do Andrew Ng’s popular machine learning Coursera. A primeira semana cobre muito, pelo menos para alguém que ainda não tocou muito cálculo para alguns anos
- Funções de Custo (diferença média ao quadrado)
- Gradiente descendente
- Regressão Linear
Estes três temas foram uma responsabilidade muito grande. Vou falar sobre cada um em detalhes, e como todos eles se encaixam, com algum código python para demonstrar.
editar 4 de Maio: Eu publiquei uma continuação focando em como a função de custo funciona aqui, incluindo uma intuição, como calculá-la manualmente e duas implementações Python diferentes. Posso fazer descida de gradiente e depois juntá-los para uma regressão linear em breve.
Modelo de Representação
Primeiro, o objetivo da maioria dos algoritmos de aprendizado é para a construção de um modelo: uma hipótese que pode ser usado para estimar Y baseado em X. A hipótese ou modelo, mapas de entradas para saídas. Então, por exemplo, digamos que eu formo um modelo baseado em um monte de dados de habitação que inclui o tamanho da casa e o preço de venda. Treinando um modelo, posso dar-lhe uma estimativa de quanto pode vender a sua casa com base no seu tamanho. Este é um exemplo de um problema de regressão — dada alguma entrada, queremos prever uma saída contínua.
A hipótese é geralmente apresentado como

theta valores são os parâmetros.
Alguns exemplos rápidos de como visualizamos a hipótese de:
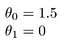
Isso produz h(x) = 1.5 + 0x. 0x significa sem declive, e y será sempre a constante 1.5. Isso parece:

Como sobre
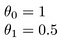

O objetivo da criação de um modelo é a escolha de parâmetros, ou theta valores, de modo que h(x) é próximo ao de y para os dados de treinamento, x e y. Portanto, para esta data
x =
y =

vou tentar e encontrar uma linha de melhor ajuste através de regressão linear. Vamos começar.
função de custo
precisamos de uma função que irá minimizar os parâmetros sobre o nosso conjunto de dados. Uma função comum que é frequentemente utilizada é o erro quadrático médio, que mede a diferença entre o estimador (o conjunto de dados) e o valor estimado (a previsão). Parece-se com isto.:

acontece Que, nós podemos ajustar a equação um pouco para fazer o cálculo, a pista um pouco mais simples. Vamos acabar com:
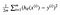
Vamos aplicar esta const função para o acompanhamento de dados:

Por agora, vamos calcular alguns valores de theta, e plotar a função de custo com a mão. Uma vez que esta função passa por (0, 0), estamos apenas olhando para um único valor da theta. A partir de Agora, vou me referir à função de custo como J (Θ).
para J (1), nós obtemos 0. Nenhuma surpresa — um valor de J (1) produz uma linha reta que se encaixa perfeitamente nos dados. Que tal J (0.5)?

O MSE função nos dá um valor de 0,58. Vamos traçar os nossos valores até agora:
J(1) = 0
J ( 0, 5) = 0.58

eu vou em frente e calcular alguns valores de J(Θ).

E se podemos juntar os pontos muito bem juntos…

podemos ver que a função de custo é, no mínimo, quando theta = 1. Isto faz sentido-os nossos dados iniciais são uma linha recta com um declive de 1 (a linha laranja na figura acima).
Gradient Descent
we minimized J (Θ) by trial and error above — just trying lots of values and visualmente inspecting the resulting graph. Deve haver uma maneira melhor? Inclinação do gradiente da fila. Descida de gradiente é uma função geral para minimizar uma função, neste caso a função de custo de erro médio ao quadrado.
descida gradiente basicamente faz apenas o que estávamos fazendo à mão — alterar os valores teta, ou parâmetros, pouco a pouco, até que esperamos chegar ao mínimo.
começamos por inicializar theta0 e theta1 a quaisquer dois valores, digamos 0 para ambos, e vamos a partir daí. Formalmente, o algoritmo é o seguinte:

onde α, alpha, é a taxa de aprendizagem, ou quão rapidamente nós deseja mover para o mínimo. Se α é muito grande, no entanto, podemos ultrapassar.

juntando tudo isso — Regressão Linear
Rapidamente resumindo:
temos uma hipótese:

o que precisamos ajustar nossos dados de treinamento. Podemos usar uma função de custo tal erro médio ao quadrado:

o que podemos minimizar o uso de gradiente descendente:

o Que leva-nos para a nossa primeira máquina de algoritmo de aprendizagem, a regressão linear. A última peça do quebra-cabeça que precisamos resolver para ter um modelo de regressão linear de trabalho é a derivação parcial da função de custo:
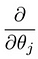
o Que acaba por ser:
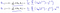
o Que nos dá regressão linear!
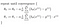
Com a teoria do caminho, eu vou ir para implementar essa lógica em python no próximo post.
Edit May 4th: I published a follow up focusing on how the Cost Function works here, including an intuition, how to calculate it by hand and two different Python implementations. Posso fazer descida de gradiente e depois juntá-los para uma regressão linear em breve.