Editor Note: Tony Abbey teach live NAFEMS FEA classes in the U. S., Europe and Asia. Ele também ensina aulas de E-learning NAFEMS globalmente. Contacto .para mais detalhes.
Um ambiente de Trabalho anterior de Engenharia de artigo (“Simplificar FEA Modelos de Simulação Usando Simetria Planar”), explicou que, mesmo com poderosos computadores modernos, muitas vezes há uma motivação para o uso de técnicas de simplificação estrutural a análise de elementos finitos (FEA). Este acompanhamento descreve como dois métodos intimamente relacionados podem ser usados para tomar 2 fatias de 2D através de uma estrutura complexa em regiões de interesse. Os modelos da FEA resultantes podem dar uma visão valiosa sobre as tensões locais mais rápida e eficientemente do que um modelo 3D completo. Eles não vão contar a história toda, mas são ferramentas valiosas para o engenheiro CAE.
os dois métodos da FEA são chamados de tensão plana e tensão plana. Ambos usam elementos planos 2D que se parecem com elementos de concha fina e são misturados usando geometria de superfície planar.
Análise De Esforço Plano
Fig. 1 mostra os fatos importantes sobre a análise de stress plano. Assume-se que a região estrutural se situa no plano 2D xy, com a terceira dimensão estrutural relativamente pequena. Na figura, esta é a espessura na direção z. Tensões existem no plano 2D como sigma x, sigma y (tensões diretas) e sigma xy (tensão de cisalhamento em plano). Cada uma destas tensões é constante através da espessura como mostrado no inset. Além disso, não pode haver estresse na direção z. Esta relação material tensão-tensão é definida em elementos de tensão plano 2D utilizados neste tipo de análise.
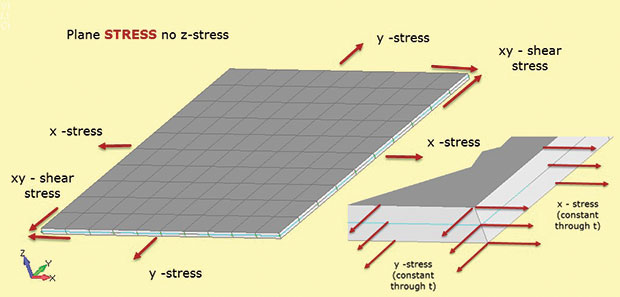Fig. 1: Tensão do Plano; pressupostos do Estado de tensão.the lack of z stress is the way to remember the element type designation plane stress (i.e. only in-plane stresses allowed). Também não há através da espessura do esforço transverso. Podíamos carregar o modelo de stress aéreo na Fig. 1 com um bi-axial de carga e calcular sigma x e sigma y. Não há sigma z. Nós também podemos calcular a correspondente no plano de cepas e-x e-y. Se aplicarmos uma carga de cisalhamento, podemos encontrar a força de cisalhamento sigma xy e tensão de cisalhamento e-xy. Curiosamente, também podemos calcular a estirpe de espessura através de e-Z. Isto não é zero, uma vez que o modelo é livre de diluir em z à medida que se estende em x e Y. não há nenhuma restrição fora de plano para evitar isso. Em alguns solvers nós podemos recuperar a estirpe através da espessura e-z e usá-la para calcular a mudança na espessura. (Se o modelo estiver em compressão Bi-axial, então a seção z ficará mais espessa). Esta é geralmente considerada uma estirpe secundária e pode não estar disponível para saída—mas está lá e pode ser calculada manualmente, se necessário.
Fig. 2 mostra um componente de alumínio. O lug protura a partir de uma chapa composta que tem planas posicionadas e ligadas sobre o tangs (ou pernas) e a secção inferior da carroçaria. A tangs transfere a carga aplicada à lug para a estrutura composta. Na prática, os plies seriam pisados para permitir uma transferência suave de cisalhamento através da ligação para o composto. A transferência de cisalhamento para o composto é simulada aqui por forças de tração de superfície difusa “puxando” no tangs. Estes balanceiam a carga de lug aplicada.
a principal suposição aqui é que através de tensões de espessura são zero e as tensões no plano são constantes através de espessura no componente. Isto significa que o detalhe local da transferência de carga de cisalhamento de compósito para tang é mal modelado. No entanto, o foco desta análise é verificar o dimensionamento da seção transversal de lug e tang longe do composto, usando tensões no plano.
a espessura do componente é pequena em comparação com outras dimensões. Este valor é dado como a espessura real na definição do elemento de tensão do plano.
Fig. 3 mostra o modelo FEA e as tensões máximas calculadas. As áreas de interesse são em torno do lug e os raios do ombro. No mundo real, o estado de estresse nas concentrações de estresse seria 3D e através da espessura sigma z estresse e tensão de cisalhamento equilibraria localmente. No entanto, é muito razoável assumir aqui que as tensões internas dominam. Esta é a mesma suposição implícita nos cálculos mais tradicionais de concentração de esforço (Kt) encontrados em manuais.
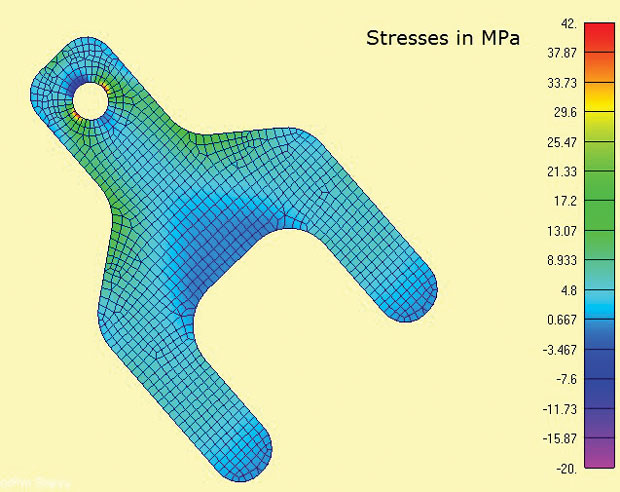Fig 3: Plano 2D estresse elementos mostrando máximo principais salientaUma das características convenientes de avião análise de tensões é que é estritamente 2D análise, portanto, apenas três graus de liberdade (DOF) tem que ser restrita (in-plane traduções x, y e rotação em torno do eixo z). Isto presta-se ao método de restrição mínima 3-2-1 com carga equilibrada. Em um caso 2D isso degenera para um método 2-1. Um nó tem DOF x e y limitados, um segundo nó ortogonal apropriado tem DOF x Restrito. Isto permite que a carga de reação no tangs seja aplicada diretamente como cargas de equilíbrio difusas. Seria difícil simular esta condição de fronteira através de restrições ao solo.
a estirpe e-z através da espessura e-z e, portanto, o desbaste da tangs podem ser calculados como um efeito secundário.
Análise De Estirpes Planas
Fig. 4 mostra a essência do método de deformação plano. Mais uma vez, elementos planos 2D são usados, mas com subtilmente diferentes pressupostos. O In-plane stresses x, y E xy são desenvolvidos como antes. No entanto, desta vez é a estirpe fora-de-plano ou através da espessura z que é definida como zero. Então, a análise da estirpe de avião só permite estirpes no plano. Isto funciona bem para representar estruturas espessas como mostrado. A presença desta quantidade de material tende a estabilizar o componente e evitar que ele se esgote em Z. Isto também significa que constante através de tensões de espessura z são desenvolvidos na estrutura. Esta relação material de tensão de tensão é definida em elementos de tensão de plano 2D utilizados neste tipo de análise.
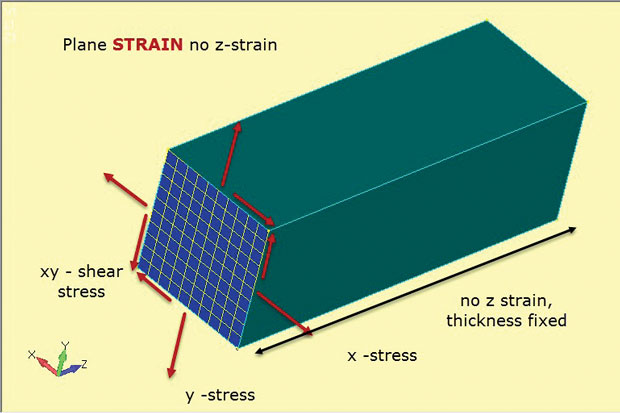Fig. 4: Análise da estirpe plana; hipóteses de stress e de estado da estirpe.a figura mostra a orientação dos elementos de deformação do plano 2D como uma secção de corte através de um componente profundo típico. A suposição é que o estado de estresse nesta seção de corte será duplicado em qualquer corte plano xy (estação z) através do componente. Assume-se que o componente é prismático (com uma secção transversal constante) até ao seu comprimento.
na prática, usamos este método onde o estado de stress varia lentamente de plano a plano num componente profundo. Deve haver material suficiente através da profundidade para estabilizar e eliminar a tensão através da espessura. Este é o mesmo princípio usado em amostras de resistência à fratura mostradas na figura. 5. Uma falha em condições de tensão plana é mostrada para a seção central da amostra espessa. A falha nas bordas livres e na seção fina é um modo diferente, mais como um estado de tensão plano. Um modelo plano de estirpe FEA seria, por definição, uma boa representação do comportamento do espécime espesso da linha central, mas não das bordas livres ou do espécime fino.
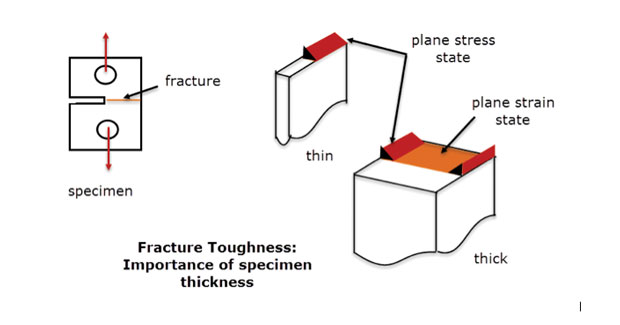Fig. 5: amostras de resistência à fractura; secções finas e grossas.Fig. 6 mostra outro componente usado em uma estrutura composta, formando uma junta aderente. Aqui a seção é constante e profunda o suficiente para que possamos assumir que as tensões também são constantes com a profundidade. A superfície da extremidade livre (at + z, – z) terá um estado de estresse local diferente (really plane stress, as noted), entretanto o objetivo desta análise é verificar a seção líquida stresses na linha central (z = 0).
a malha de análise de estirpes de plano 2D é mostrada no componente 3D da Fig. 7. O corte da secção é definido na estação z = 0.
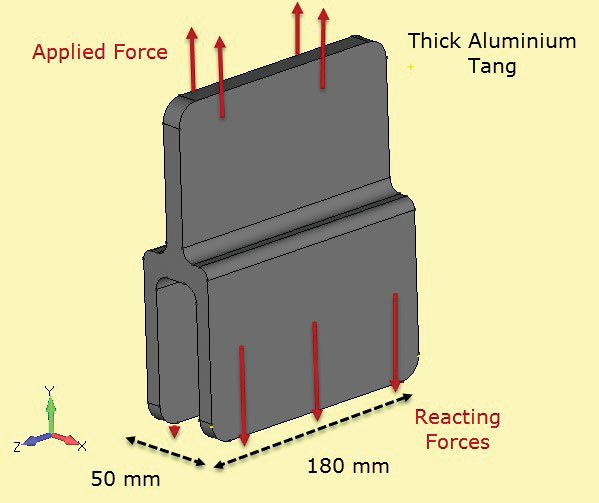Fig. 6: tangente de alumínio de secção profunda.
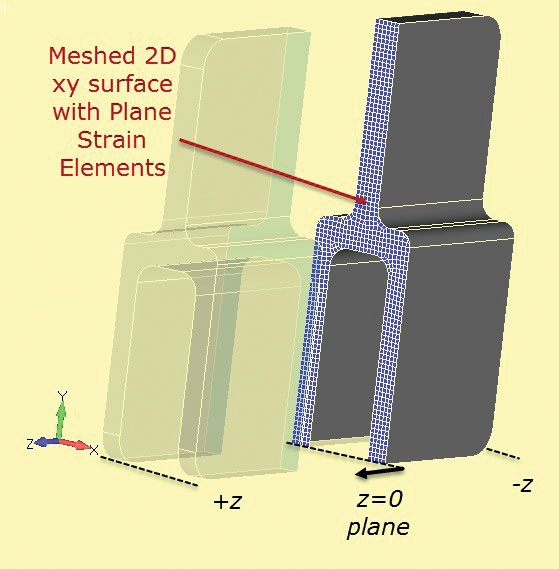Fig. 7: Secção cortada através da secção sólida para desenvolver a secção de deformação do plano 2D.pode ser utilizada uma malha de deformação de plano 2D muito fina, que funcionará muito rapidamente em comparação com um modelo 3D completo. O método de restrição 2-1 é usado como antes. O carregamento deve ser considerado cuidadosamente. A “espessura” da seção de tensão do plano é bastante arbitrária, e é geralmente definido em 1,0 por padrão. Se a carga no componente for calculada como uma carga de execução através da profundidade (N/m, Lbf/polegada, etc.) então este valor pode ser usado diretamente na malha de deformação plano. É útil escolher uma secção, como a tang única e estimar a tensão nominal ou média nesta secção para o componente completo. Isto pode ser usado como um teste de sanidade na análise de estirpes de plano. O carregamento incorrecto é provavelmente a principal causa de erro neste método.
os resultados da análise são apresentados na Fig. 8 e mostrar claramente as regiões de alta tensão em torno do filete do ombro. As tensões são válidas para a região de profundidade central do componente (z = 0).
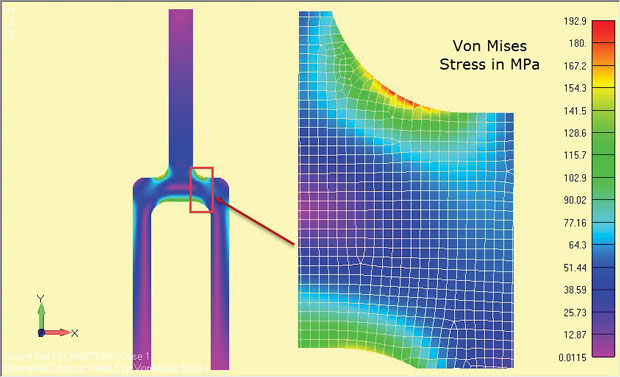Fig. 8: Análise de esforço plano resultados de um componente de Tang profundo.as quantidades de stress utilizadas dependerão da solução utilizada. Alguns solucionadores ignoram as tensões de direção z como secundário e recuperam as tensões no plano. The principal stresses and von Mises stresses then relate to a 2D in-plane stress state. Se a tensão da direção z for recuperada, então ela deve ser claramente identificada, de modo que o estado de tensão 2D no plano X-y possa ser identificado.
o que exatamente o estresse de direção z representa? É o estresse desenvolvido devido à aplicação da tensão de direção z zero. O estresse age como se as faces livres da seção prismática fossem fixas. No plano central de um componente de secção profunda, estas serão as tensões complementares necessárias para manter o estado de tensão Da Direcção zero Z. Na realidade, à medida que nos movemos em direção às faces livres da superfície, o estresse z cai para zero e torna-se uma distribuição de estresse plano (como visto na espessa amostra mecânica de fraturas).
em muitos casos, tais como um cilindro pressurizado, as faces finais são cobertas e irão de fato desenvolver uma tensão axial devido a forças axiais. Este será um estresse diferente do estresse axial induzido na análise de deformação plano. Será necessário um cálculo manual para calcular as tensões axiais, ou possível um modelo axisimétrico suplementar para recipientes sob pressão.
a facilidade de geometria e construção da malha se presta bem a estudos “o que-se” ou mais estudos formais de otimização da forma.
para comparação, uma análise 3D completa de meia simetria do componente de Tang profundo foi feita e os resultados são mostrados na Fig. 9. A tensão nominal através da perna Tang única superior é idêntica em ambos os casos—lembre-se que esta é a base de qualquer verificação de sanidade.
as tensões locais no ombro são menores em uma pequena porcentagem no modelo completo. Isto é por três razões. Em primeiro lugar, a malha tet 3D relativamente grosseira é inferior à malha local muito fina de deformação plana 2D. Não foi realizada uma verificação de convergência do modelo 3D.
em segundo lugar, há uma pequena alteração na geometria nas superfícies livres (+z,- z) em comparação com a secção z = 0 devido aos filetes finais. Neste caso, o efeito é negligenciável, uma vez que os filetes estão longe das regiões do ombro. Em muitos componentes, no entanto, haverá filetes locais, e ficar sem detalhes. que irá variar a geometria de uma simples face XY planar. Variações locais de estresse nas faces de extremidade livre podem ter que ser estimadas ou verificadas com um modelo 3D completo.
finalmente, a assunção da tensão plana de uma restrição z fixa a +z,-Z seções não é verdadeira para um componente de profundidade finita. A tensão z se difunde para zero nas faces livres “reais”. Este efeito é mostrado na Fig. 10, que usa o modelo 3D como é e também como uma simulação da tensão da estirpe de plano z.
Fast and Efficient
Plane stress and plane strain analyses are useful 2D methods that can often supplement full-scale 3D models. Nem todos os recursos podem ser representados, mas com alguma ingenuidade, tensões em áreas-chave podem pelo menos ser estimados. A motivação para usar os métodos é permitir uma análise rápida e eficiente com fácil geometria 2D e construção de malha.