O campo elétrico E pode sempre ser expresso como o gradiente de uma função potencial escalar
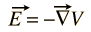
não Há gerais escalar potencial para o campo magnético B, mas pode ser expressa como a curvatura de uma função de vetor
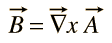
Esta função é dado o nome de “potencial vetor” mas ele não está diretamente associada com o trabalho o caminho que escalar potencial.
o potencial vetorial é definido como sendo consistente com a Lei de Ampere e pode ser expresso em termos de corrente I ou densidade de corrente j (as fontes do campo magnético). Em vários textos, esta definição assume as formas
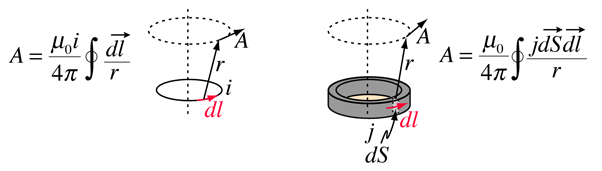
uma razão para o potencial vetorial é que pode ser mais fácil calcular o potencial vetorial do que calcular o campo magnético diretamente a partir de uma dada geometria de corrente de fonte. Sua aplicação mais comum é a teoria da antena e a descrição das ondas eletromagnéticas.
Desde que o campo magnético B é definido como a onda de Um, e o vetor de identidade a curvatura de um gradiente é identicamente igual a zero, então qualquer função arbitrária que pode ser expresso como o gradiente de uma função escalar pode ser adicionado a Um sem alterar o valor de B obtido a partir dele. Isto é, Um’ pode ser livremente substituído por Uma onde
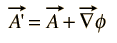
Tais transformações são chamadas de transformações de calibre, e tem havido um número de “medidores”, que têm sido utilizados para vantagem é a tipos específicos de cálculos na teoria eletromagnética.