Encontrar una solución óptima para ciertos problemas de optimización puede ser una tarea increíblemente difícil, a menudo prácticamente imposible. Esto se debe a que cuando un problema es lo suficientemente grande, necesitamos buscar una enorme cantidad de soluciones posibles para encontrar la óptima. Incluso con la potencia informática moderna, a menudo hay demasiadas soluciones posibles que considerar. En este caso, debido a que no podemos esperar de manera realista encontrar el óptimo dentro de un período de tiempo razonable, tenemos que conformarnos con algo que esté lo suficientemente cerca.
Un problema de optimización de ejemplo que generalmente tiene un gran número de soluciones posibles sería el problema del vendedor ambulante. Para encontrar una solución a un problema como el de un vendedor ambulante, necesitamos usar un algoritmo que sea capaz de encontrar una solución lo suficientemente buena en un tiempo razonable. En un tutorial anterior vimos cómo podríamos hacer esto con algoritmos genéticos, y aunque los algoritmos genéticos son una forma de encontrar una solución «lo suficientemente buena» para el problema de los vendedores ambulantes, hay otros algoritmos más simples que podemos implementar que también nos encontrarán una solución cercana a la óptima. En este tutorial, el algoritmo que usaremos es ‘recocido simulado’.
Si no está familiarizado con el problema del vendedor ambulante, puede que valga la pena echar un vistazo a mi tutorial anterior antes de continuar.
¿Qué es el recocido simulado?
En primer lugar, veamos cómo funciona el recocido simulado y por qué es bueno para encontrar soluciones al problema del vendedor ambulante en particular. El algoritmo de recocido simulado se inspiró originalmente en el proceso de recocido en trabajos de metal. El recocido consiste en calentar y enfriar un material para alterar sus propiedades físicas debido a los cambios en su estructura interna. A medida que el metal se enfría, su nueva estructura se fija, lo que hace que el metal retenga sus propiedades recién obtenidas. En el recocido simulado, mantenemos una variable de temperatura para simular este proceso de calentamiento. Inicialmente lo configuramos alto y luego permitimos que se «enfríe» lentamente a medida que se ejecuta el algoritmo. Si bien esta variable de temperatura es alta, se permitirá al algoritmo, con más frecuencia, aceptar soluciones que son peores que nuestra solución actual. Esto le da al algoritmo la capacidad de saltar de cualquier óptimo local en el que se encuentre al principio de la ejecución. A medida que se reduce la temperatura, también lo es la posibilidad de aceptar soluciones peores, lo que permite que el algoritmo se enfoque gradualmente en un área del espacio de búsqueda en la que, con suerte, se pueda encontrar una solución cercana a la óptima. Este proceso de «enfriamiento» gradual es lo que hace que el algoritmo de recocido simulado sea notablemente efectivo para encontrar una solución cercana a la óptima cuando se trata de grandes problemas que contienen numerosos óptimos locales. La naturaleza del problema del vendedor ambulante lo convierte en un ejemplo perfecto.
Ventajas del recocido simulado
Es posible que se pregunte si hay alguna ventaja real en la implementación del recocido simulado sobre algo como un simple escalador de colinas. Aunque los escaladores de colinas pueden ser sorprendentemente efectivos para encontrar una buena solución, también tienen una tendencia a quedarse atascados en los óptimos locales. Como determinamos anteriormente, el algoritmo de recocido simulado es excelente para evitar este problema y es mucho mejor en promedio para encontrar un óptimo global aproximado.
Para ayudar a comprender mejor, echemos un vistazo rápidamente a por qué un algoritmo básico de escalada en colinas es tan propenso a quedar atrapado en los óptimos locales.
Un algoritmo de escalador de colinas simplemente aceptará soluciones vecinas que son mejores que la solución actual. Cuando el escalador no puede encontrar mejores vecinos, se detiene.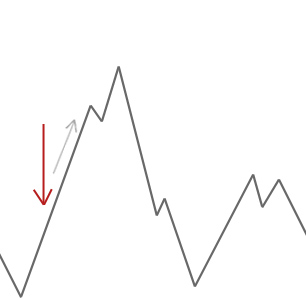
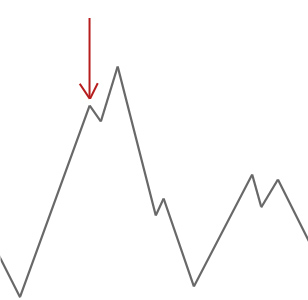
En el ejemplo anterior, comenzamos nuestro escalador de colinas en la flecha roja y se abre camino hasta la colina hasta que alcanza un punto en el que no puede subir más alto sin primero descender. En este ejemplo podemos ver claramente que está atascado en un óptimo local. Si esto fuera un problema del mundo real, no sabríamos cómo se ve el espacio de búsqueda, por lo que desafortunadamente no podríamos decir si esta solución está cerca de un óptimo global.
El recocido simulado funciona de manera ligeramente diferente a esto y ocasionalmente aceptará soluciones peores. Esta característica del recocido simulado lo ayuda a saltar de cualquier óptimo local en el que de otro modo podría haberse atascado.
Función de aceptación
Echemos un vistazo a cómo el algoritmo decide qué soluciones aceptar para que podamos comprender mejor cómo es capaz de evitar estos óptimos locales.
Primero comprobamos si la solución vecina es mejor que nuestra solución actual. Si lo es, lo aceptamos incondicionalmente. Sin embargo, si la solución vecina no es mejor, debemos considerar un par de factores. En primer lugar, cuánto peor es la solución vecina; y en segundo lugar, cuán alta es la «temperatura» actual de nuestro sistema. A altas temperaturas, es más probable que el sistema acepte soluciones que son peores.
La matemática para esto es bastante simple:
Básicamente, cuanto menor sea el cambio en la energía (la calidad de la solución), y cuanto mayor sea la temperatura, más probable será que el algoritmo acepte la solución.
Descripción general del algoritmo
¿Cómo se ve el algoritmo? Bueno, en su implementación más básica es bastante simple.
- Primero necesitamos establecer la temperatura inicial y crear una solución inicial aleatoria.
- Luego comenzamos a hacer un bucle hasta que se cumpla nuestra condición de parada. Por lo general, el sistema se ha enfriado lo suficiente o se ha encontrado una solución lo suficientemente buena.
- Desde aquí seleccionamos un vecino haciendo un pequeño cambio en nuestra solución actual.
- Luego decidimos si nos movemos a esa solución vecina.
- Finalmente, disminuimos la temperatura y seguimos en bucle
Inicialización de temperatura
Para una mejor optimización, al inicializar la variable de temperatura, debemos seleccionar una temperatura que inicialmente permita prácticamente cualquier movimiento contra la solución actual. Esto le da al algoritmo la capacidad de explorar mejor todo el espacio de búsqueda antes de enfriarse y establecerse en una región más enfocada.
Código de ejemplo
Ahora usemos lo que sabemos para crear un algoritmo de recocido simulado básico, y luego aplíquelo al problema del vendedor ambulante a continuación. Vamos a usar Java en este tutorial, pero esperamos que la lógica sea lo suficientemente simple como para copiarla en cualquier idioma de su elección.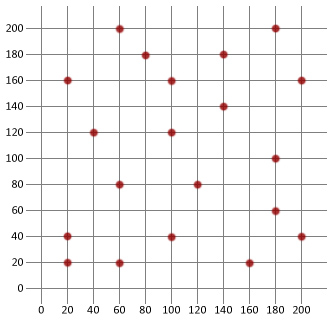
Primero necesitamos crear una clase de ciudad que se pueda usar para modelar los diferentes destinos de nuestro vendedor ambulante.
Ciudad.java
* Ciudad.java
* Modelos a ciudad
* /
paquete sa;
ciudad de clase pública {
int x;
int y;
/ / Construye una ciudad colocada aleatoriamente
ciudad pública () {
esto.x = (int) (Math.random () * 200);
esto.y = (int) (Math.aleatorio()*200);
}
// Construye una ciudad en la ubicación x, y elegida
ciudad pública (int x, int y){
esto.x = x;
esto.y = y;
}
// Obtiene la coordenada x de la ciudad
public int getX () {
devuelve esto.x;
}
// Obtiene la coordenada y de la ciudad
public int getY () {
devuelve esto.y;
}
// Obtiene la distancia a la ciudad dada
doble distancia pública a (Ciudad ciudad){
int xDistance = Math.abs (getX () – ciudad.getX());
int ydistancia = Matemáticas.abs (getY () – ciudad.getY ());
distancia doble = Matemáticas.sqrt ((xDistance * xDistance) + (yDistance*yDistance));
distancia de retorno;
}
@ Override
cadena pública toString () {
return getX ()+», «+getY();
}
}
A continuación, vamos a crear una clase que pueda hacer un seguimiento de las ciudades.
TourManager.java
* TourManager.java
* Contiene las ciudades de un tour
* /
paquete sa;
importar java.útil.ArrayList;
gestor turístico de clase pública {
/ / Mantiene nuestras ciudades
ArrayList estático privado destinationCities = nueva ArrayList< Ciudad>();
// Agrega una ciudad de destino
addCity de vacío estático público (City city) {
destinationCities.añadir (ciudad);
}
// Obtenga una ciudad
ciudad estática pública getCity (índice int){
destino de retorno (Ciudad).obtener (índice);
}
// Obtenga el número de ciudades de destino
número int estático público de ciudades () {
devolver ciudades de destino.tamaño();
}
}
Ahora para crear la clase que puede modelar un viaje de vendedor ambulante.
Tour.java
* Tour.java
* Almacena un recorrido candidato a través de todas las ciudades
* /
paquete sa;
importar java.útil.ArrayList;
importar java.útil.Colecciones;
tour de clase pública{
/ / Realiza nuestro tour de ciudades
tour privado de ArrayList = ArrayList nuevo< Ciudad>();
// Cache
private int distance = 0;
/ / Construye un tour en blanco
public Tour(){
for (int i = 0; i < TourManager.numberOfCities (); i++) {
tour.añadir (nulo);
}
}
// Construye un tour a partir de otro tour
tour público (ArrayList tour){
esto.tour = tour (ArrayList).clon();
}
// Información del recorrido de retorno
ArrayList público getTour () {
recorrido de retorno;
}
// Crea un bucle individual aleatorio
public void generateIndividual() {
// a través de todas nuestras ciudades de destino y añádelas a nuestro tour
for (int CityIndex = 0; CityIndex < TourManager.numberOfCities (); CityIndex++) {
setCity(CityIndex, TourManager.getCity (CityIndex));
}
// Reordenar aleatoriamente las Colecciones de tour
.barajar (tour);
}
/ / Obtiene una ciudad del tour
Ciudad pública getCity (int tourPosition) {
tour de regreso (Ciudad).get (tourPosition);
}
// Establece una ciudad en una posición determinada dentro de un recorrido
conjunto vacío público (int tourPosition, City city) {
recorrido.set (tourPosition, city);
/ / Si los tours han sido alterados, necesitamos restablecer el estado físico y la distancia
distancia = 0;
}
// Obtiene la distancia total del recorrido
int getDistance () {
if (distance = = 0) {
int tourDistance = 0;
/ / Recorre las ciudades de nuestro recorrido
for (int CityIndex = 0; CityIndex < tourSize(); CityIndex++) {
// Get city estamos viajando desde
City fromCity = getCity(CityIndex);
// Ciudad estamos viajando a
City destinationCity;
// Compruebe que no estamos en la última ciudad de nuestro recorrido, si configuramos nuestra
// la ciudad de destino final del recorrido a nuestra ciudad de inicio
if(CityIndex+1 <tourSize()){
destinationCity = getCity(CityIndex+1);
}
else{
destinationCity = getCity(0);
}
// Obtenga la distancia entre las dos ciudades
tourDistance + = fromCity.Distancia a (Ciudad de destino);
}
distancia = Distancia turística;
}
distancia de retorno;
}
// Obtenga el número de ciudades en nuestro tour
public int tourSize () {
tour de regreso.tamaño();
}
@Reemplazar
public String toString() {
String geneString = «|»;
for (int i = 0; i < tourSize(); i++) {
geneString += getCity(i)+»|»;
}
volver geneString;
}
}
Finalmente, vamos a crear nuestro algoritmo de recocido simulado.
Recuperación simulada.paquete java
SimulatedAnnealing de clase pública {
/ / Calcule la probabilidad de aceptación
aceptabilidad de doble aceptación estática pública (int energy, int NewEnergy, double temperature) {
/ / Si la nueva solución es mejor, acéptela
if (NewEnergy < energy) {
retorno 1.0;
}
// Si la nueva solución es peor, calcule una probabilidad de aceptación
devuelve matemáticas.exp ((energy-NewEnergy) / temperature);
}
public static void main(String args) {
// Crea y agrega nuestras ciudades
City city = new City(60, 200);
TourManager.addCity(ciudad);
City city2 = ciudad nueva (180, 200);
TourManager.addCity (city2);
City city3 = ciudad nueva(80, 180);
TourManager.addCity (city3);
City city4 = ciudad nueva(140, 180);
TourManager.addCity (city4);
City city5 = ciudad nueva(20, 160);
TourManager.addCity (city5);
City city6 = ciudad nueva(100, 160);
TourManager.addCity (city6);
City city7 = ciudad nueva(200, 160);
TourManager.addCity (city7);
City city8 = new City(140, 140);
TourManager.addCity (city8);
City city9 = ciudad nueva(40, 120);
TourManager.Ciudad adicional (ciudad 9);
City city10 = ciudad nueva (100, 120);
TourManager.addCity (city10);
City city11 = ciudad nueva(180, 100);
TourManager.addCity (city11);
City city12 = ciudad nueva(60, 80);
TourManager.addCity (city12);
City city13 = ciudad nueva(120, 80);
TourManager.addCity (city13);
City city14 = ciudad nueva(180, 60);
TourManager.addCity (city14);
City city15 = ciudad nueva(20, 40);
TourManager.addCity (city15);
City city16 = ciudad nueva(100, 40);
TourManager.addCity (city16);
City city17 = ciudad nueva(200, 40);
TourManager.Ciudad adicional (ciudad17);
City city18 = ciudad nueva (20, 20);
TourManager.addCity (city18);
City city19 = ciudad nueva(60, 20);
TourManager.addCity (city19);
City city20 = ciudad nueva(160, 20);
TourManager.addCity (city20);
// Establecer temperatura inicial
doble temperatura = 10000;
// Velocidad de enfriamiento
velocidad de enfriamiento doble = 0.003;
// Inicializar solución inicial
Tour currentSolution = new Tour ();
Solución actual.generateIndividual ();
System.fuera.println («Distancia inicial de la solución:» + Solución actual.getDistance ());
// Establecer como mejor actual
Tour best = nuevo Tour(Solución actual.getTour ());
// Bucle hasta que el sistema se haya enfriado
mientras (temp > 1) {
// Crear nuevo tour vecino
Tour newSolution = nuevo Tour (Solución actual.getTour ());
// Obtener posiciones aleatorias en el tour
int tourPos1 = (int) (Solución de noticias.tourSize () * Math.random ());
int tourPos2 = (int) (Solución de noticias.tourSize () * Math.random ());
/ / Obtener las ciudades en las posiciones seleccionadas en el tour
City citySwap1 = newSolution . getCity (tourPos1);
City citySwap2 = newSolution . getCity (tourPos2);
// Swap them
Solución de noticias.setCity (tourPos2, citySwap1);
Solución de noticias.setCity (tourPos1, citySwap2);
// Obtener energía de soluciones
int currentEnergy = currentSolution.getDistance ();
int neighbourEnergy = newSolution.getDistance ();
/ / Decide si debemos aceptar el vecino
if (Aceptaciónprobabilidad (energía actual, energía vecina, temp) > Matemáticas.random()) {
currentSolution = new Tour (Solución de noticias.getTour());
}
// Mantenga un registro de la mejor solución encontrada
if (Solución actual.getDistance () < mejor.getDistance ()) {
best = new Tour (Solución actual.getTour());
}
// Sistema de enfriamiento
temp * = 1-Tasa de enfriamiento;
}
Sistema.fuera.println(«Distancia de solución final:» + mejor.getDistance());
System.fuera.println («Tour:» + mejor);
}
}
Salida
Distancia de solución final: 911
Recorrido: |180, 200/200, 160/140, 140/180, 100/180, 60/200, 40/160, 20/120, 80/100, 40/60, 20/20, 20/20, 40/60, 80/100, 120/40, 120/20, 160/60, 200/80, 180/100, 160/140, 180|
Conclusión
En este ejemplo pudimos alcanzar más de la mitad de la distancia de nuestra ruta inicial generada aleatoriamente. Esperamos que esto muestre lo útil que es este algoritmo relativamente simple cuando se aplica a ciertos tipos de problemas de optimización.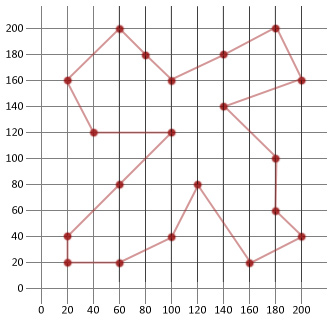
Autor
 Hola, soy Lee.
Hola, soy Lee.Soy un desarrollador del Reino Unido que ama la tecnología y los negocios. Aquí encontrarás artículos y tutoriales sobre cosas que me interesan. Si quieres contratarme o saber más sobre mí, dirígete a mi página acerca de mí