probabil cea mai utilizată valoare într-un raport de sol este capacitatea portantă a solului. Motivul evident este că exemplele de bază date în majoritatea cărților de text folosesc aproape întotdeauna capacitatea portantă pentru a calcula dimensiunea planului unei baze. Datorită simplității și ușurinței de utilizare, această metodă este în continuare parametrul fundamental al solului pentru proiectarea fundației. Cu toate acestea, această simplitate presupune că piciorul se va comporta ca un corp rigid. Această presupunere specială funcționează bine în practică pentru fundații mici și cu o singură coloană. Dar pentru fundațiile mari și cu mai multe coloane, majoritatea inginerilor preferă analiza flexibilă. Calculul Manual al analizei flexibile ar putea fi o provocare și, în aproape toate cazurile, programe software precum STAAD, SAFE, GT STRUDL etc. sunt folosite. Cu toate acestea, aceste programe de calculator solicită adesea o intrare numită „modul de reacție subgradă”. Mulți ingineri nu sunt familiarizați cu acest termen și încearcă adesea să-l compare cu capacitatea portantă. Deoarece tot mai mulți Ingineri vor folosi software pentru a proiecta fundații, este esențial ca inginerii să aibă o înțelegere fundamentală a acestui parametru al solului. Există vreo relație între capacitatea portantă și modulul reacției subgrade?
modulul reacției Subgrade (Ks)
acest termen este măsurat și exprimat ca intensitate a sarcinii pe unitatea de deplasare. Pentru sistemul de unități englez, acesta este adesea exprimat în kip/in2/in; în sistemul SI este exprimat ca kN/m2/m. unii exprimă acest termen în kip/in3 (sau kN/m3) care poate fi înșelător. Numeric, kip / in3 este corect, dar nu reprezintă în mod corespunzător semnificația fizică a valorii măsurate și ar putea fi confundat ca o unitate de densitate sau o măsurare volumetrică.
matematic, coeficientul de reacție subgradă este exprimat ca:
Ks = p/s (Eqn 1)
unde p = intensitatea presiunii de contact și s = așezarea solului
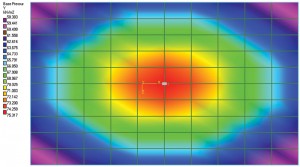
figura 1a: diagrama de deviere și conturul presiunii solului.
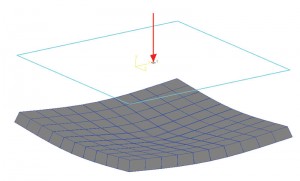
figura 1b: conturul presiunii solului.
după cum a menționat Terzaghi, estimarea corectă a presiunii de contact pentru o fundație flexibilă ar putea fi foarte greoaie, deci se presupune că Ks rămâne constantă pentru întreaga bază. Cu alte cuvinte, raportul dintre presiune și decontare în toate locațiile unui picior va rămâne constant. Deci, diagrama de deplasare a unui picior cu o sarcină în centru va avea un efect de dishing. Un punct din centrul piciorului va experimenta cea mai mare deplasare. Deplasarea se reduce pe măsură ce se îndepărtează de centru. Figura 1a prezintă o fundație simplă pe placă. A fost modelat și analizat în Fundația STAAD ca „Mat”, care este o fundație flexibilă; solul a fost definit folosind coeficientul de reacție subgradă. Pentru acest exercițiu, a fost utilizată valoarea implicită a software-ului pentru modulul de reacție subgradă. Diagrama de deplasare arată un efect de dishing așa cum sa discutat mai devreme. Figura 1b prezintă conturul presiunii solului. De asemenea, este evident că intensitatea presiunii în centru este maximă și se reduce pe măsură ce elementele (sau coordonatele nodului) se îndepărtează de centru. Deci, s-ar putea presupune că raportul dintre intensitatea presiunii și decontare este constant.
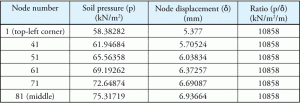
Tabelul 1: presiunea solului, deplasarea nodului și raportul acestora.
luați în considerare unele dintre numerele din același exemplu. Presiunea solului, deplasarea corespunzătoare și raportul sunt enumerate în tabelul 1. Punctele sunt reprezentate pe o diagonală pentru a ilustra variația presiunii și deplasării pe măsură ce punctele se îndepărtează de centru până la cel mai îndepărtat punct din colțul piciorului dreptunghiular. Figura 2 prezintă punctele de pe placa mat.
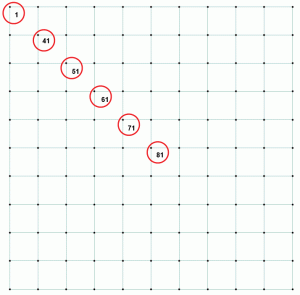
Figura 2: Puncte selectate pentru a compara presiunea de bază, deformarea și raportul.
aceasta nu este deloc o surpriză, deoarece, prin definiție, modulul reacției subgrade (Ks) este o constantă pentru întreaga bază și programul a folosit Ks ca proprietate a solului. De asemenea, este important să rețineți că valoarea KS implicită a software-ului (10858 kN/m2/m) a fost exact aceeași cu raportul constant calculat în tabelul 1.
presiunea de bază a fost calculată din reacția de susținere. S-ar putea crede că raportul dintre reacția de sprijin și deplasarea corespunzătoare va fi, de asemenea, o constantă. După cum se arată în tabelul 2, raporturile nu sunt constante pentru toate valorile. Cum se utilizează valoarea Ks în interiorul programului și cum se calculează presiunea de bază?
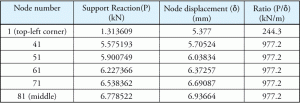
Tabelul 2: reacția de susținere și deplasarea.
zona afluentă
adesea se face o presupunere pentru a calcula câtă suprafață a unei plăci poate fi atribuită unui nod sau, cu alte cuvinte, influența fiecărui nod asupra suprafeței unei plăci. Depinde de forma plăcii. Pentru o placa patrata sau dreptunghiulara perfecta, fiecare nod va influenta cu exactitate aria suprafetei placii (figura 3a). Dar pentru un patrulater generalizat, cea mai bună practică ar fi calcularea Centrului masei plăcii și apoi trasarea liniilor de la acel punct central la punctele de mijloc ale fiecărei părți. În figura 3b, zona umbrită reprezintă suprafața de influență a nodului corespunzător.
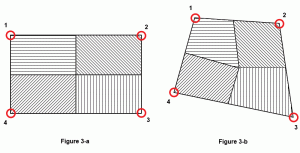
Figura 3: Zona afluentă a nodului.
Constanta suportului arcului
calculul suprafeței afluente descris mai sus este procedura cheie utilizată intern de software-ul comercial pentru a calcula constanta arcului liniar. Programul calculează mai întâi aria afluentă pentru fiecare nod al bazei și apoi înmulțește modulul reacției subgrade cu aria afluentă corespunzătoare pentru fiecare nod pentru a obține constanta arcului liniar la fiecare nod.
Kyi = Ks X Tai (Eqn 2)
unde
Kyi este constanta arcului la nodul ith
Tai este zona de influență a nodului ith
Ks este modulul reacției subgrade
pentru o analiză a fundației concrete, aceste arcuri trebuie să fie definit ca doar prin compresie, deoarece se presupune că betonul nu poartă nicio forță de tracțiune. Presiunea de bază este calculată la fiecare nod de sprijin prin împărțirea reacției de sprijin cu zona afluentă a nodului corespunzător. Dacă ne uităm la exemplul de mai sus, nodul 1 are o zonă afluentă mult mai mică decât restul nodurilor. De asemenea, se poate observa că toate celelalte noduri au aceeași zonă afluentă. Aceasta explică Tabelul 2, deoarece arată că raportul pentru nodul 1 este diferit de alte noduri. Figura 4 prezintă zona afluentă pentru diferite noduri. Nodul 1 are o suprafață afluentă care este de 25% din nodul 81. Tabelul 3 este o extensie a tabelelor 1 și 2 și arată modul în care raportul constant este atins pentru toate nodurile.
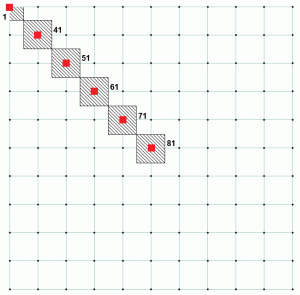
Figura 4: Zona afluentă a nodurilor selectate.
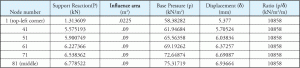
Tabelul 3: reacția, presiunea de bază, deplasarea, Constanta Ks.
decontare admisibilă
capacitatea portantă este măsurarea presiunii solului pe care un sol o poate suporta în siguranță. Cu alte cuvinte, capacitatea portantă este presiunea pe care solul o poate rezista înainte de a eșua. Cele mai importante două criterii de eșec al solului sunt:
- eșec forfecare
- decontare maximă admisibilă
printre mulți factori, lățime fundație (B) poate influența criteriile de eșec. În mod normal, eșecul de forfecare guvernează fundațiile mai mici, iar eșecul de decontare guvernează fundațiile mai mari. Tabelul 4 este un exemplu tipic care arată relația dintre diferitele dimensiuni ale fundației și criteriile de eșec.
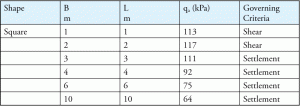
Tabelul 4: capacitatea portantă finală admisibilă pentru decontarea admisibilă = 25 mm și o adâncime de încorporare dată.
pentru a estima eșecul de decontare, se presupune o valoare de decontare admisibilă (în mod normal 25 mm sau 1 inch). Când solul se stabilește mai mult decât valoarea admisibilă, solul eșuează. Deci, chiar și pentru un calcul al capacității portante, se folosește o așezare admisibilă a solului, iar inginerii structurali ar trebui să fie conștienți de această valoare în timp ce proiectează o bază. Valoarea admisibilă de decontare a solului este de obicei o parte integrantă a oricărui raport de sol.
de ce să folosiți modulul de reacție Subgradă
s-a afirmat anterior că pentru a proiecta o fundație mată flexibilă, modulul de reacție subgradă este utilizat în locul capacității portante a solului. Dar de ce? Răspunsul constă în ipotezele care stau la baza modului în care s-ar putea comporta o fundație.
fundațiile pot fi rigide sau flexibile. Capacitatea portantă este utilizată pentru a proiecta fundații rigide, dar reacția subgradă este utilizată pentru fundații flexibile. Însăși presupunerea unei fundații rigide este că ” distribuția reacției subgrade p peste baza fundației trebuie să fie plană, deoarece o fundație rigidă rămâne plană atunci când se așează.”Luați în considerare un fascicul pur și simplu susținut încărcat în centrul său, așa cum se arată în figura 5a. prin statică, putem obține R1 = P/2 și R2 = P/2. Dacă același fascicul este încărcat excentric, reacția poate fi calculată așa cum se arată în figura 5b.
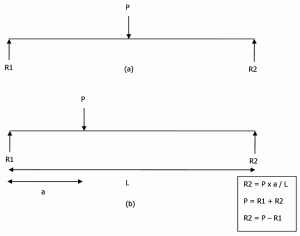
Figura 5: Reacții pentru un fascicul pur și simplu susținut.
același concept este extins pentru proiectarea rigidă a fundației. Dar, în loc de suporturile finale, întreaga fundație este susținută. De asemenea, se presupune că rigiditatea relativă a plăcii de beton este mult mai mare decât rigiditatea solului. Deci, se presupune că placa rămâne plană chiar și după aplicarea încărcăturii.
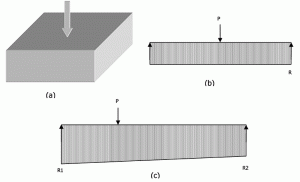
Figura 6: reacții de grad inferior pentru o bază izolată.
figura 6a prezintă un picior încărcat în centru. Dintr-o analogie rigidă cu fascicul larg, P = R x L. În mod similar, pentru o bază încărcată excentric, reacția va varia liniar de la un capăt la altul, așa cum se arată în figura 6c. ecuațiile 3 și 4 pot fi rezolvate pentru a găsi reacții finale. Dar niciuna dintre ecuații nu conține modulul reacției subgrade (Ks). Deci, „distribuția reacției subgrade pe baza unei baze rigide este independentă de gradul de compresibilitate al subgradului” pe care se sprijină. După cum au concluzionat mulți autori, o fundație rigidă poate fi proiectată în siguranță folosind capacitatea portantă, deoarece în majoritatea cazurilor această metodă dă rezultate mai conservatoare.
P = 1/2l(R1 + R2) (Eqn 3)
P X a = 1/6b2r1 + 1/3b2r2 (Eqn 4)
dar o fundație mată este adesea concepută ca o fundație flexibilă, deoarece poate fi de dimensiuni mari și pot exista multe puncte de aplicare a sarcinii și alte complexități, inclusiv găuri și grinzi de grad. Disponibilitatea pe scară largă a software-ului FEA contribuie la această tendință. Dar, spre deosebire de fundațiile rigide, o fundație flexibilă nu poate avea reacție liniară subgradă. Mai degrabă, depinde de compresibilitatea fundației, precum și de rigiditatea structurală. O fundație flexibilă este supusă îndoirii interne și deplasărilor relative între două puncte ale plăcii. Cu cât rigiditatea structurală este mai mare, cu atât este mai mică deplasarea relativă. Autorul a testat carcasa cu o rigiditate foarte mare a elementelor plăcii, rezultând o suprafață aproape plană după aplicarea sarcinii. În mod similar, cu cât modulul reacției subgrade este mai mare, cu atât distribuția presiunii este mai mică. Cu alte cuvinte, o valoare Ks mai mare va absorbi mai multă presiune la punctul de aplicare a sarcinii. Prin urmare, modulul de reacție subgradă,care este funcția de așezare a solului și presiunea externă, este utilizat pentru proiectarea flexibilă a fundației.
corelații
cel mai frecvent – și probabil cel mai sigur – răspuns la întrebarea corelației dintre capacitatea portantă și modulul reacției subgrade este că nu există nicio corelație. Dar ar trebui să existe unul, deoarece ambele sunt măsurătorile capacităților solului și oricare dintre acești doi parametri poate fi utilizat pentru a proiecta o fundație regulată.
din nou, definiția Ks este presiunea pe unitate de decontare. Cu alte cuvinte, capacitatea solului de a rezista presiunii pentru o deplasare dată. Din discuțiile anterioare, este, de asemenea, clar că chiar și capacitatea portantă are o decontare admisibilă. Prin urmare, este tentant să concluzionăm că modulul reacției subgrade este capacitatea portantă pe unitate de decontare.
această concluzie este foarte asemănătoare cu ecuația prezentată de Bowles.
SI: Ks = 40(SF)qa kN/m3 (Eqn 5)
FPS: Ks = 12(SF)qa k/ft3 (eqn 6)
unde SF = factorul de siguranță și qa este capacitatea portantă admisibilă.
în ecuațiile 5 și 6, capacitatea portantă admisibilă este mai întâi convertită în capacitatea portantă finală prin înmulțirea cu un factor de siguranță. Autorul a presupus o așezare de un inch sau 25 mm. Ecuația finală este apoi formulată împărțind capacitatea portantă finală la decontarea presupusă.
forma mai generică a ecuației poate fi scrisă ca:
Ks = 
stres/deplasare (Eqn 7)
unde
I = factor de siguranță
ac este capacitatea portantă admisibilă
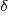este decontarea admisibilă a solului
aceste ecuații indică în mod clar că trebuie utilizat factorul de siguranță adecvat, iar valoarea KS poate fi mai bună în comparație cu capacitatea portantă finală, mai degrabă decât capacitatea portantă admisibilă. Factorul de siguranță poate varia în funcție de proiecte și ingineri geotehnici. Celălalt factor important este decontarea admisibilă presupusă pentru capacitatea portantă calculată.
în mod similar, trebuie remarcat faptul că valorile presiunii de bază raportate prin analiza FEA nu pot fi comparate direct cu capacitatea portantă. Presiunea maximă de bază trebuie înmulțită cu factorul de siguranță și apoi comparată cu capacitatea portantă admisibilă a solului.
cu toate acestea, ecuațiile menționate mai sus au limitări. Acestea pot fi aplicate la fundații în care guvernează eșecul de decontare, dar nu pot fi legate de fundații în care eșecul de forfecare are loc înainte de a atinge limita de decontare admisibilă. Deci, inginerii trebuie să fie precauți înainte de a utiliza aceste ecuații.
concluzie
corelația dintre capacitatea portantă și modulul reacției subgrade este în cel mai bun caz o estimare. Poate fi utilizat pentru estimare, dar o valoare Ks determinată printr-un test de încărcare a plăcii trebuie utilizată întotdeauna dacă este disponibilă sau trebuie solicitată ori de câte ori este posibil. Cu toate acestea, discuția de mai sus oferă o perspectivă asupra acestor valori și îi ajută pe ingineri să înțeleagă semnificația fizică a modulului de reacție subgrad. Și, ca întotdeauna, inginerii structurali ar trebui să consulte un inginer geotehnic profesionist înainte de a finaliza rigiditatea solului și valorile rulmentului.▪