Simplificación de modelos de FEA: Tensión Plana y Deformación Plana

Nota del editor: Tony Abbey enseña clases de FEA de NAFEMS en vivo en los EE.UU., Europa y Asia. También imparte clases de aprendizaje electrónico de NAFEMS en todo el mundo. Contacto .para más detalles.

Un artículo anterior de Ingeniería de Escritorio («Simplify FEA Simulation Models Using Planar Symmetry») explicó que incluso con computadoras modernas poderosas, a menudo hay una motivación para usar técnicas de simplificación en el análisis de elementos finitos estructurales (FEA). Este seguimiento describe cómo se pueden usar dos métodos estrechamente relacionados para tomar cortes 2D a través de una estructura compleja en regiones de interés. Los modelos de AEF resultantes pueden proporcionar información valiosa sobre las tensiones locales de manera más rápida y eficiente que un modelo 3D completo. No contarán toda la historia, pero son herramientas valiosas para el ingeniero CAE.

Los dos métodos FEA se denominan tensión plana y deformación plana. Ambos utilizan elementos planos en 2D que parecen elementos de concha delgada y están mallados con geometría de superficie plana.

Análisis de tensiones planas

Fig. 1 muestra los hechos importantes sobre el análisis de tensiones planas. Se supone que la región estructural se encuentra en el plano 2D xy, con la tercera dimensión estructural relativamente pequeña. En la figura, este es el grosor en la dirección z. Existen tensiones en el plano 2D como sigma x, sigma y (tensiones directas) y sigma xy (tensión de corte en el plano). Cada una de estas tensiones es constante a través del espesor como se muestra en el recuadro. Además, no puede haber estrés en la dirección z. Esta relación material tensión-deformación se define en elementos planos de tensión 2D utilizados en este tipo de análisis.

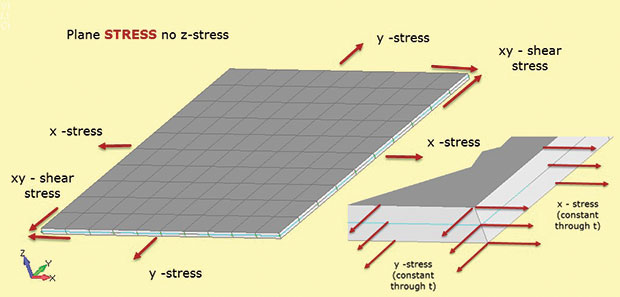Fig. 1: Estrés plano; suposiciones de estado de estrés.

La falta de tensión z es la forma de recordar la tensión plana de designación de tipo de elemento (es decir, solo se permiten tensiones en el plano). Tampoco hay tensiones de corte de espesor pasante. Podríamos cargar el modelo de tensión plana en la Fig. 1 con una carga biaxial y calcular sigma x y sigma y. No hay sigma z. También podemos calcular las correspondientes deformaciones en el plano e-x e e-y. Si aplicamos una carga de cizallamiento, podemos encontrar la tensión de cizallamiento sigma xy y la tensión de cizallamiento e-xy. Curiosamente, también podemos calcular la deformación de espesor pasante e-z. Esto no es cero, ya que el modelo es libre de adelgazar en z a medida que se estira en x e y. No hay restricción fuera del plano para evitar esto. En algunos solucionadores podemos recuperar la deformación de espesor pasante e-z y usarla para calcular el cambio de espesor. (Si el modelo está en compresión biaxial, la sección z se volverá más gruesa). Esto generalmente se considera una cepa secundaria y puede no estar disponible para la salida—pero está ahí y se puede calcular manualmente si es necesario.

Fig. 2 muestra un componente de orejeta de aluminio. La lengüeta sobresale de una capa de lámina compuesta que tiene capas colocadas y unidas sobre las espigas (o patas) y la sección inferior del cuerpo. Las espigas transfieren la carga aplicada a la orejeta a la estructura compuesta. En la práctica, las capas se escalonarían para permitir una transferencia de cizallamiento suave a través de la unión hacia el compuesto. La transferencia de cizallamiento en el compuesto se simula aquí mediante fuerzas de tracción de superficie difusas «tirando» de las espigas. Estos equilibran la carga de orejetas aplicada.

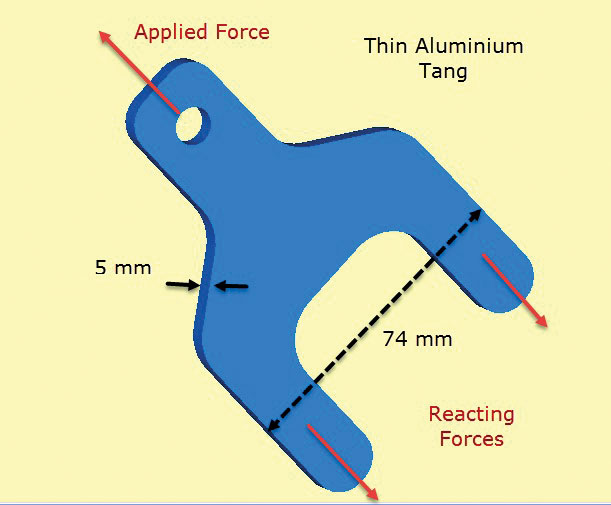Fig. 2: Espiga de aluminio de paredes delgadas que transfiere carga a una estructura compuesta.

El supuesto clave aquí es que las tensiones de espesor pasante son cero y las tensiones en el plano son constantes en el espesor del componente. Esto significa que el detalle local de la transferencia de carga de corte del compuesto al espiga está mal modelado. Sin embargo, el objetivo de este análisis es comprobar el tamaño de la sección transversal de la espiga y la espiga del compuesto, utilizando esfuerzos en el plano.

El grosor del componente es pequeño en comparación con otras dimensiones. Este valor se introduce como el grosor real en la definición del elemento de tensión plana.

Fig. 3 muestra el modelo de AEF y las tensiones principales máximas calculadas. Las áreas de interés están alrededor de la lengüeta y los radios de los hombros. En el mundo real, el estado de tensión en las concentraciones de tensión sería 3D y, a través del espesor, las tensiones sigma z y las tensiones de corte se equilibrarían localmente. Sin embargo, es muy razonable suponer aquí que dominan las tensiones en el plano. Esta es la misma suposición implícita en la mayoría de los cálculos tradicionales de concentración de esfuerzo (Kt) que se encuentran en los manuales.

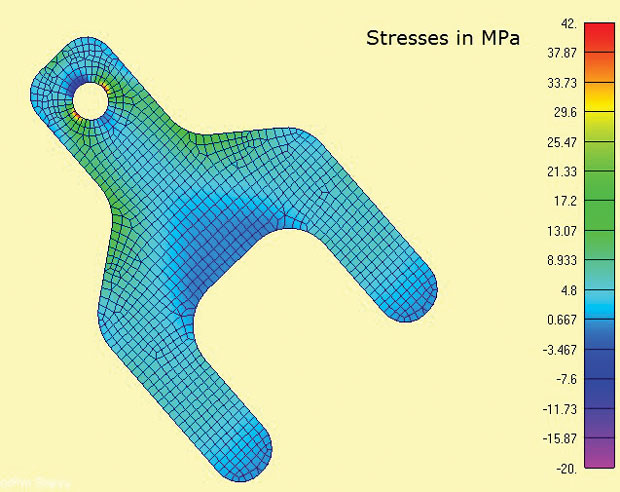Figura 3: Elementos de tensión plana 2D que muestran tensiones principales máximas

Una de las características convenientes del análisis de tensión plana es que es un análisis estrictamente 2D, por lo que solo se deben restringir tres grados de libertad (DOF) (traslaciones en el plano x, y y rotación sobre el eje z). Esto se presta al método de restricción mínima 3-2-1 con carga equilibrada. En un caso 2D, esto degenera en un método 2-1. Un nodo tiene DOF x e y restringido, un segundo nodo ortogonal apropiado tiene DOF x restringido. Esto permite que la carga de reacción en las espigas se aplique directamente como cargas de equilibrado difusas. Sería difícil simular esta condición de frontera a través de restricciones al suelo.

La deformación de espesor pasante e-z y, por lo tanto, el adelgazamiento de las espigas podrían calcularse como un efecto secundario.

Análisis de deformación plana

Fig. 4 muestra la esencia del método de deformación plana. De nuevo, se utilizan elementos planos 2D, pero con suposiciones sutilmente diferentes. Las tensiones en el plano x, y y xy se desarrollan como antes. Sin embargo, esta vez es la deformación z fuera de plano o a través del espesor la que se establece en cero. Por lo tanto, el análisis de deformación plana solo permite deformaciones en el plano. Esto funciona bien para representar estructuras gruesas como las mostradas. La presencia de tanto material tiende a estabilizar el componente y evitar que se tense en z. Esto también significa que se desarrollan tensiones constantes de espesor z en la estructura. Esta relación material tensión-deformación se define en los elementos planos de deformación 2D utilizados en este tipo de análisis.

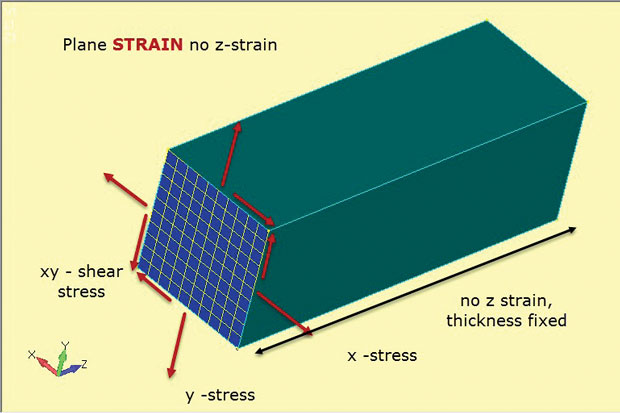Fig. 4: Análisis de deformación plana; suposiciones de estado de tensión y deformación.

La figura muestra la orientación de los elementos planos de deformación 2D como sección de corte a través de un componente profundo típico. La suposición es que el estado de tensión en esta sección de corte se duplicará en cualquier corte plano xy (estación z) a través del componente. Se supone que el componente es prismático (tiene una sección transversal constante) en su longitud.

En la práctica, utilizamos este método donde el estado de tensión varía lentamente de un plano a otro en un componente profundo. Debe haber suficiente profundidad de material para estabilizar y eliminar la deformación de espesor pasante. Este es el mismo principio utilizado en las muestras de resistencia a la fractura que se muestran en la Fig. 5. Se muestra una falla en condiciones de deformación plana para la sección central de la muestra gruesa. La falla en los bordes libres y la sección delgada es un modo diferente, más como un estado de tensión plana. Un modelo FEA de deformación plana sería, por definición, una buena representación del comportamiento de la espécimen gruesa de la línea central, pero no de los bordes libres o de la espécimen delgada.

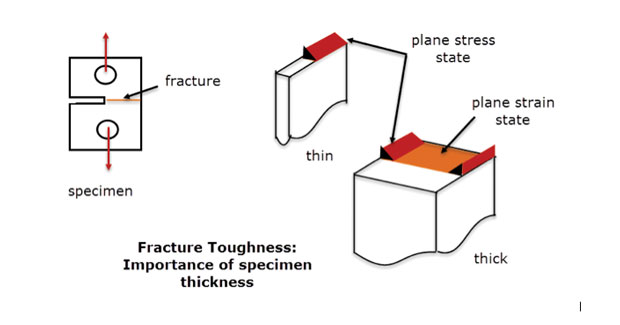Fig. 5: Muestras de tenacidad a la fractura; secciones finas y gruesas.

Fig. 6 muestra otro componente utilizado en una estructura compuesta, formando una junta unida. Aquí la sección es constante y lo suficientemente profunda para que podamos asumir que las tensiones también son constantes con la profundidad. Las caras de la superficie del extremo libre (en +z, -z) tendrán un estado de tensión local diferente (en realidad tensión plana, como se señaló), sin embargo, el objetivo de este análisis es verificar las tensiones de la sección neta en la línea central (z = 0).

La malla de análisis de deformación plana 2D se muestra seccionada en el componente 3D en la Fig. 7. El corte de sección se define en la estación z = 0.

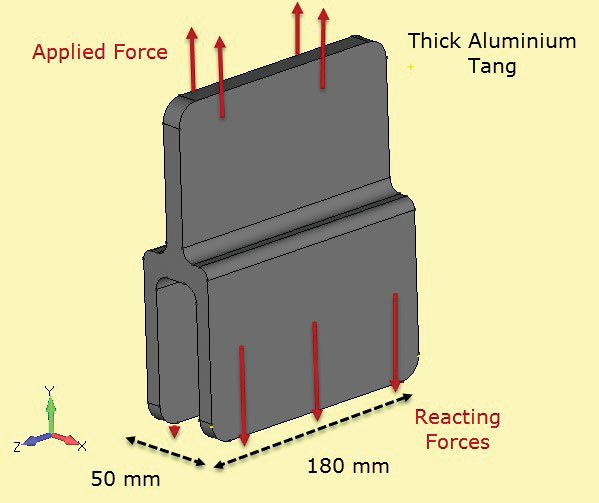Fig 6: Espiga de aluminio de sección profunda.

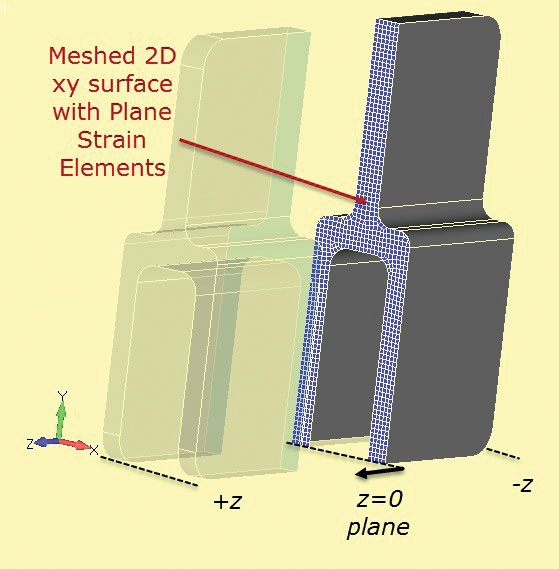Fig. 7: Sección cortada a través de una sección sólida para desarrollar una sección de deformación plana 2D.

Se puede usar una malla de deformación plana 2D muy fina, que funcionará muy rápidamente en comparación con un modelo 3D completo. El método de restricción 2-1 se usa como antes. La carga debe considerarse cuidadosamente. El» grosor » de la sección de deformación plana es bastante arbitrario, y generalmente se establece en 1.0 por defecto. Si la carga en el componente se calcula como una carga de funcionamiento a través de la profundidad(N / m, Lbf / pulgada, etc.) a continuación, este valor se puede utilizar directamente en la malla de deformación plana. Es útil elegir una sección, como la espiga única y estimar la tensión nominal o media en esta sección para el componente completo. Esto se puede utilizar como un control de cordura en el análisis de deformación plana. La carga incorrecta es probablemente la principal causa de error en este método.

Los resultados del análisis se muestran en la Fig. 8 y mostrar claramente las regiones de alto estrés alrededor del filete de hombro. Las tensiones son válidas para la región de profundidad central del componente (z = 0).

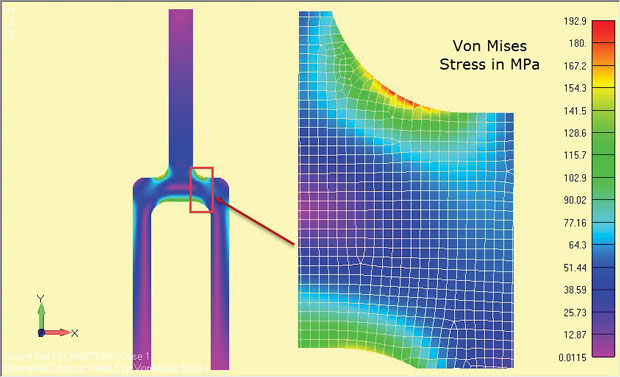Fig. 8: Resultados de análisis de deformación plana de un componente de espiga profunda.

Las cantidades de tensión utilizadas dependerán del solucionador utilizado. Algunos solucionadores ignoran las tensiones de dirección z como secundarias y recuperan las tensiones en el plano. Las tensiones principales y las tensiones de von Mises se relacionan entonces con un estado de tensión en el plano 2D. Si se recupera la tensión en dirección z, debe identificarse claramente, de modo que se pueda identificar el estado de tensión en el plano 2D en el plano x-y.

¿Qué representa exactamente la tensión de dirección z? Es la tensión desarrollada debido a la aplicación de la deformación en dirección z cero. La tensión actúa como si los extremos libres de la sección prismática fueran fijos. En el plano central de un componente de sección profunda, estas serán las tensiones complementarias necesarias para mantener el estado de deformación en dirección z cero. En realidad, a medida que nos movemos hacia las caras de la superficie libre, la tensión z cae a cero y se convierte en una distribución de tensión plana (como se ve en la muestra de mecánica de fractura gruesa).

En muchos casos, como en un cilindro presurizado, las caras de los extremos están tapadas y, de hecho, desarrollarán una tensión axial debido a fuerzas axiales. Este será un esfuerzo diferente del esfuerzo axial inducido en el análisis de deformación plana. Se necesitará un cálculo manual para calcular las tensiones axiales, o posiblemente un modelo axisimétrico suplementario para recipientes a presión.

La facilidad de la geometría y la construcción de malla se presta bien a estudios hipotéticos o estudios de optimización de formas más formales.

Para la comparación, se realizó un análisis 3D completo de media simetría del componente tang profundo y los resultados se muestran en la Fig. 9. La tensión nominal a través de la pata de espiga única superior es idéntica en ambos casos; recuerde que esta es la base de cualquier comprobación de cordura.

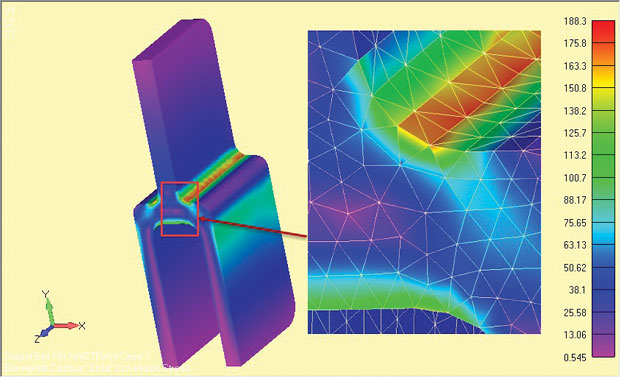Fig. 9: Modelo 3D completo de la espiga profunda, mostrando resultados de estrés.

Las tensiones locales del hombro son inferiores en un pequeño porcentaje en el modelo completo. Esto se debe a tres razones. En primer lugar, la malla tet 3D relativamente gruesa es inferior a la malla local de deformación plana 2D muy fina. No se ha realizado un control de convergencia en el modelo 3D.

En segundo lugar, hay un pequeño cambio en la geometría en las superficies libres (+z,- z) en comparación con la sección z = 0 debido a los filetes finales. En este caso, el efecto es insignificante, ya que los filetes están lejos de las regiones del hombro. En muchos componentes, sin embargo, habrá filetes locales y se agotarán los detalles. que variará la geometría de una simple cara plana xy. Las variaciones de tensión locales en los extremos libres pueden tener que estimarse o comprobarse con un modelo 3D completo.

Finalmente, la suposición de deformación plana de una restricción z fija en secciones +z,-z no es cierta para un componente de profundidad finita. La tensión z se difundirá a cero en las caras libres «reales». Este efecto se muestra en la Fig. 10, que utiliza el modelo 3D tal cual y también como simulación de la tensión z de deformación plana.

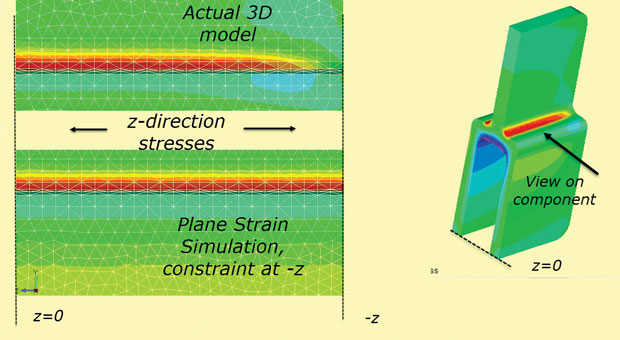Fig. 10: Difusión de la tensión z hacia la superficie libre.

Los análisis de tensión plana y deformación plana rápidos y eficientes

son métodos 2D útiles que a menudo pueden complementar los modelos 3D a gran escala. No se pueden representar todas las características, pero con un poco de ingenio, al menos se pueden estimar las tensiones en áreas clave. La motivación para utilizar los métodos es permitir un análisis rápido y eficiente con una geometría 2D fácil y una construcción de malla.