förmodligen är det mest använda värdet i en jordrapport jordbärande kapacitet. Det uppenbara skälet är att grundläggande exempel som ges i de flesta läroböcker nästan alltid använder bärighet för att beräkna plandimensionen på en fot. På grund av enkelhet och användarvänlighet är denna metod fortfarande den grundläggande jordparametern för grunddesign. Men den enkelheten förutsätter att foten kommer att fungera som en stel kropp. Det specifika antagandet fungerar bra i praktiken för små och enkla kolonnfot. Men för stora och flera kolumnfundament föredrar de flesta ingenjörer flexibel analys. Manuell beräkning av flexibel analys kan vara utmanande och i nästan alla fall program som STAAD, SAFE, GT STRUDL etc. används. Men dessa datorprogram ber ofta om en ingång som kallas ”modulus of subgrade reaction”. Många ingenjörer är inte bekanta med denna term och försöker ofta jämföra den med bärkraft. Eftersom fler och fler ingenjörer kommer att använda programvara för att utforma fundament är det viktigt för ingenjörer att ha en grundläggande förståelse för denna jordparameter. Finns det något samband mellan bärighet och modul för undergrundsreaktion?
modul för Undergrundsreaktion (Ks)
denna term mäts och uttrycks som belastningsintensitet per förskjutningsenhet. För det engelska enhetssystemet uttrycks det ofta i kip/in2/in; i SI-systemet uttrycks det som kN/m2/m. vissa uttrycker denna term i kip/in3 (eller kN / m3) vilket kan vara vilseledande. Numeriskt är kip / in3 korrekt men representerar inte korrekt den fysiska betydelsen av det uppmätta värdet och kan misstas som en densitetsenhet eller en volymetrisk mätning.
matematiskt uttrycks koefficienten för undergrundsreaktion som:
Ks = p / s (Eqn 1)
där p = kontakttrycksintensitet och s = jordavveckling
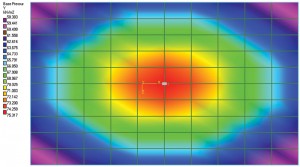
Figur 1a: Avböjningsdiagram och marktryckskontur.
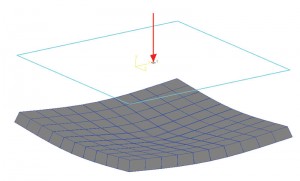
Figur 1b: Jordtryckskontur.
som Terzaghi nämnde kan korrekt uppskattning av kontakttryck för en flexibel grund vara mycket besvärlig, så det antas att Ks förblir konstant för hela foten. Med andra ord, förhållandet mellan tryck och avveckling på alla platser i en fot kommer att förbli konstant. Så förskjutningsdiagrammet för en fot med en belastning i mitten kommer att ha en diskningseffekt. En punkt i mitten av foten kommer att uppleva den högsta förskjutningen. Förskjutningen minskar när den rör sig bort från mitten. Figur 1a visar en enkel platta-on-grade foundation. Den modellerades och analyserades i STAAD Foundation som ”matta”, som är en flexibel grund; jorden definierades med hjälp av koefficient för undergrundsreaktion. För denna övning användes standardvärdet för programvaran för modulen för undergrundsreaktion. Förskjutningsdiagrammet visar en diskningseffekt som diskuterats tidigare. Figur 1b visar markens tryckkontur. Det är också uppenbart att tryckintensiteten i mitten är maximal och minskar när elementen (eller nodkoordinaterna) rör sig bort från mitten. Så det kan antas att förhållandet mellan tryckintensitet och avveckling är konstant.
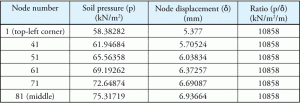
Tabell 1: marktryck, nodförskjutning och deras förhållande.
Tänk på några av siffrorna från samma exempel. Marktryck, motsvarande förskjutning och förhållandet anges i Tabell 1. Punkterna representeras på en diagonal för att illustrera variationen i tryck och förskjutning när punkterna rör sig bort från mitten till den mest avlägsna punkten i hörnet av den rektangulära foten. Figur 2 visar punkterna på mattan plattan.
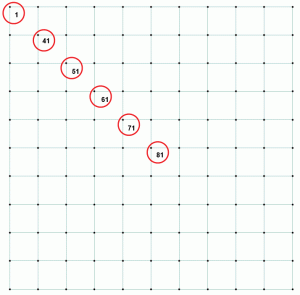
Figur 2: Valda punkter för att jämföra bastryck, avböjning och förhållande.
detta är knappast en överraskning, eftersom per definition modulen för subgrade reaction (Ks) är en konstant för hela foten och programmet använde Ks som sin jordegenskap. Det är också viktigt att notera att programvarans standard ks-värde (10858 kN/m2/m) var exakt detsamma som det konstanta förhållandet beräknat i Tabell 1.
bastryck beräknades från stödreaktionen. Man kan tro att förhållandet mellan stödreaktion och motsvarande förskjutning också kommer att vara en konstant. Som visas i Tabell 2 är förhållandena inte konstanta för alla värden. Hur används Ks-värdet i programmet och hur beräknas bastrycket?
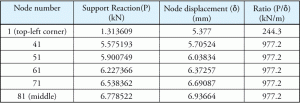
Tabell 2: Stödreaktion och förskjutning.
Biflodsområde
ofta görs ett antagande för att beräkna hur mycket område av en platta som kan hänföras till en nod eller med andra ord påverkan av varje nod på ytan på en platta. Det beror på plattans form. För en perfekt kvadratisk eller rektangulär platta, kommer varje nod att påverka exakt XXL av plattans yta (figur 3a). Men för en generaliserad fyrkant skulle den bästa praxisen vara att beräkna mitten av plattans massa och sedan rita linjer från den mittpunkten till mittpunkterna på varje sida. I figur 3b representerar det skuggade området inflytningsytan för motsvarande nod.
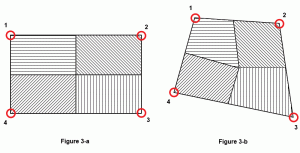
Figur 3: nod biflod område.
Fjäderstödskonstant
den ovan beskrivna beräkningen av biflodsområdet är den viktigaste proceduren som används internt av den kommersiella programvaran för att beräkna den linjära Fjäderkonstanten. Programmet beräknar först biflodsområdet för varje nod på foten och multiplicerar sedan modulen för undergrundsreaktion med motsvarande biflodsområde för varje nod för att få den linjära Fjäderkonstanten vid varje nod.
Kyi = Ks x Tai (Eqn 2)
där
Kyi är Fjäderkonstanten vid ith-noden
Tai är inflytningsområdet för ith-noden
Ks är modulen för undergrundsreaktion
för en betongfundamentanalys måste dessa fjädrar vara definieras som endast kompression, eftersom betong antas inte bära någon dragkraft. Bastrycket beräknas vid varje stödnod genom att dividera stödreaktionen med motsvarande nodbiflodsområde. Om vi tittar på ovanstående exempel har nod 1 ett mycket mindre biflodområde än resten av noderna. Det kan också noteras att alla andra noder har samma biflodsområde. Detta förklarar Tabell 2, eftersom det visar förhållandet för nod 1 är annorlunda än andra noder. Figur 4 visar biflodsområdet för olika noder. Nod 1 har ett biflodområde som är 25% av Nod 81. Tabell 3 är en förlängning av tabellerna 1 och 2 och visar hur konstant förhållande uppnås för alla noder.
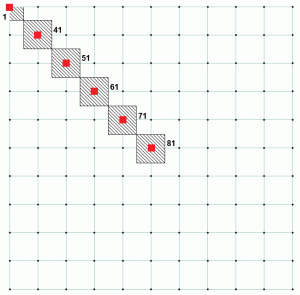
Figur 4: Biflodsområde för valda noder.
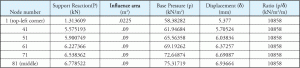
tabell 3: reaktion, bastryck, förskjutning, Ks konstant.
tillåten avveckling
bärighet är mätningen av marktrycket som en jord säkert kan bära. Med andra ord är bärighet det tryck som jorden tål innan den misslyckas. De två viktigaste kriterierna för markfel är:
- Skjuvfel
- Maximal tillåten lösning
bland många faktorer kan grundbredden (B) påverka felkriterier. Normalt styr skjuvfel för mindre stiftelser och bosättningsfel styr större stiftelser. Tabell 4 är ett typiskt exempel som visar förhållandet mellan olika grundstorlekar och felkriterier.
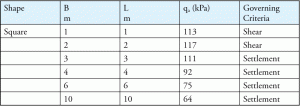
Tabell 4: slutlig tillåten bärighet för tillåten settlement = 25 mm och ett givet inbäddningsdjup.
för att uppskatta avvecklingsfel antas ett tillåtet avvecklingsvärde (normalt 25 mm eller 1 tum). När jorden sätter sig mer än det tillåtna värdet misslyckas jorden. Så även för en bärkapacitetsberäkning används en tillåten markuppgörelse och konstruktörer bör vara medvetna om det värdet när de utformar en fot. Det tillåtna markavvecklingsvärdet är vanligtvis en integrerad del av varje markrapport.
Varför använda modulen för Undergrundsreaktion
det har tidigare angetts att för att utforma en flexibel mattfundament används modulen för undergrundsreaktion istället för bärighet av jord. Men varför? Svaret ligger i de underliggande antagandena om hur en stiftelse kan bete sig.
fundament kan vara styva eller flexibla. Bärförmåga används för att utforma styva fundament, men undergrundsreaktion används för flexibla fundament. Själva antagandet om en styv grund är att ” fördelningen av undergrundsreaktionen p över fundamentets bas måste vara plan, eftersom en styv grund förblir plan när den sätter sig.”Tänk på en helt enkelt stödd stråle laddad i centrum, som visas i figuren 5a. med Statik kan vi få R1 = P/2 och R2 = P/2. Om samma stråle laddas excentriskt kan reaktionen beräknas som visas i Figur 5b.
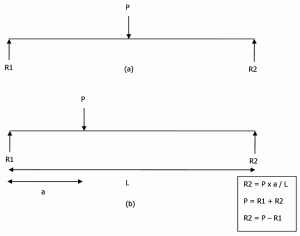
Figur 5: Reaktioner för en helt enkelt stödd stråle.
samma koncept förlängs för styv grunddesign. Men istället för slutstöden stöds hela grunden. Det antas också att betongplattans relativa styvhet är mycket högre än markstyvheten. Så antas plattan förbli plan även efter applicering av belastning.
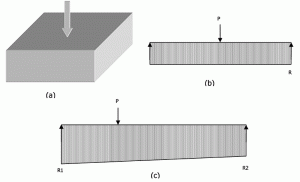
Figur 6: Sub grade reaktioner för en isolerad fot.
figur 6a visar en fot som är laddad i mitten. Från en styv bredstråleanalogi, P = R x L. På samma sätt, för en excentriskt laddad fot, kommer reaktionen att variera linjärt från ena änden till den andra som visas i Figur 6c. ekvationer 3 och 4 kan lösas för att hitta slutreaktioner. Men ingen av ekvationerna innehåller modul av subgrade reaction (Ks). Så, ”fördelningen av undergrundsreaktionen på basen av en styv fot är oberoende av graden av kompressibilitet hos undergrunden” som den vilar på. Som många författare har dragit slutsatsen kan en styv grund utformas säkert med bärkraft, eftersom den här metoden i de flesta fall ger mer konservativa resultat.
P = 1/2l(R1 + R2) (Eqn 3)
P X a = 1/6B2R1 + 1/3b2r2 (Eqn 4)
men en mattfundament är ofta utformad som en flexibel grund eftersom den kan vara stor i storlek och det kan finnas många belastningspunkter och andra komplexiteter, inklusive hål och balkar. Utbredd tillgänglighet av FEA-programvara bidrar till denna trend. Men till skillnad från styva fundament kan en flexibel grund inte ha linjär undergrundsreaktion. Snarare beror det på stiftelsens kompressibilitet såväl som den strukturella styvheten. En flexibel grund utsätts för inre böjning och relativa förskjutningar mellan två plattpunkter. Ju större strukturell styvhet desto mindre är den relativa förskjutningen. Författaren testade fallet med mycket hög styvhet av plattelementen, vilket resulterade i en nästan plan yta efter appliceringen av lasten. På samma sätt, ju större modul för undergrundsreaktion, desto mindre är tryckfördelningen. Med andra ord kommer ett högre Ks-värde att absorbera mer tryck vid belastningsapplikationspunkten. Därför används modulen för undergrundsreaktion,som är funktionen av markuppgörelse och det yttre trycket, för flexibel grunddesign.
korrelationer
det vanligaste – och förmodligen säkraste – svaret på frågan om korrelation mellan bärighet och modulen för undergrundsreaktion är att det inte finns någon korrelation. Men det borde finnas en, eftersom båda är mätningarna av markkapacitet och någon av dessa två parametrar kan användas för att utforma en vanlig grund.
återigen är definitionen av Ks trycket per enhetsavveckling. Med andra ord, jordkapacitet för att motstå tryck för en given förskjutning. Från tidigare diskussioner är det också tydligt att även bärkraft har en tillåten lösning. Det är därför frestande att dra slutsatsen att modulen för undergrundsreaktion är bärkapaciteten per enhetsavveckling.
denna slutsats är mycket lik den ekvation som presenteras av Bowles.
SI: Ks = 40 (SF)qa kN/m3(Eqn 5)
FPS: Ks = 12 (SF)qa k/ft3 (Eqn 6)
där SF = säkerhetsfaktor och qa är den tillåtna bärigheten.
i ekvationerna 5 och 6 omvandlas den tillåtna bärigheten först till den ultimata bärigheten genom att multiplicera med en säkerhetsfaktor. Författaren antog en tum eller 25 mm bosättning. Den slutliga ekvationen formuleras sedan dividera den ultimata bärighet av den antagna avvecklingen.
den mer generiska formen av ekvationen kan skrivas som:
Ks = 
stress/förskjutning (Eqn 7)
där
I = säkerhetsfaktor
qa är den tillåtna bärigheten
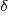är den tillåtna markuppgörelsen
dessa ekvationer indikerar tydligt att Lämplig säkerhetsfaktor måste användas, och KS-värdet kan jämföras bättre med den ultimata bärigheten snarare än den tillåtna bärigheten. Säkerhetsfaktorn kan variera beroende på projekt och geotekniska ingenjörer. Den andra viktiga faktorn är den antagna tillåtna avvecklingen för den beräknade bärkapaciteten.
på samma sätt ska det noteras att de bastryckvärden som rapporteras genom FEA-analys inte kan jämföras direkt med bärigheten. Maximalt bastryck bör multipliceras med säkerhetsfaktorn och sedan jämföras med jordens tillåtna bärkraft.
men ovanstående ekvationer har begränsningar. De kan tillämpas på fot där avvecklingsfel reglerar, men kan inte relateras till fot där skjuvfel inträffar innan den tillåtna avvecklingsgränsen uppnås. Så ingenjörer måste vara försiktiga innan de använder dessa ekvationer.
slutsats
korrelationen mellan bärighet och modul för undergrundsreaktion är i bästa fall en uppskattning. Den kan användas för uppskattning, men ett Ks-värde som bestäms av ett plåtbelastningstest bör alltid användas om det är tillgängligt eller bör begäras när det är möjligt. Ovanstående diskussion ger emellertid insikt i dessa värden och hjälper ingenjörer att förstå den fysiska betydelsen av modul för undergrundsreaktion. Och som alltid bör konstruktörer konsultera en geoteknisk ingenjör professionell innan slutföra markstyvhet och lagervärden.▪