det elektriska fältet E kan alltid uttryckas som gradienten för en skalärpotentialfunktion
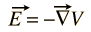
det finns ingen allmän skalärpotential för magnetfält B men det kan uttryckas som krullen för en vektorfunktion
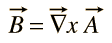
denna funktion A ges namnet ”vektorpotential” men det är inte direkt associerat med arbete som skalärpotential är.
vektorpotentialen definieras för att vara förenlig med Amperes lag och kan uttryckas i termer av antingen ström i eller strömtäthet j (magnetfältets källor). I olika texter tar denna definition formerna
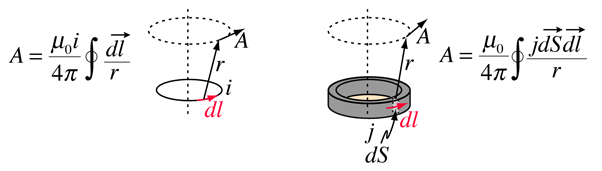
en motivering för vektorpotentialen är att det kan vara lättare att beräkna vektorpotentialen än att beräkna magnetfältet direkt från en given källströmsgeometri. Dess vanligaste tillämpning är att antennteori och beskrivningen av elektromagnetiska vågor.
eftersom magnetfältet B definieras som krökningen av A, och med vektoridentitet är krökningen av en gradient identiskt noll, kan varje godtycklig funktion som kan uttryckas som gradienten för en skalärfunktion läggas till A utan att ändra värdet på B erhållet från det. Det vill säga A ’ kan fritt ersättas med A där
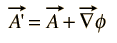
sådana transformationer kallas gauge transformationer, och det har varit ett antal ”mätare” som har använts till fördel är specifika typer av beräkningar i elektromagnetisk teori.