Holder Transformation
Holder Transformation (även ”Holder reflektion”) är en ortogonal reflektion transformation:
- det reflex vektorerna i kolumnerna i matrisen så att
- den första vektorn har alla nollor utom det första elementet
Transformationsmatrisen
Reflektionstransformation:
egenskaper
Hushållsmatriser är symmetriska och ortogonala: de är reflektionsmatriser
Derivation
så vi har $P = I-2vv^t$:
vi använder sådana omvandlingar för nollställningselement
QR-sönderdelning
som vid LU-sönderdelning, där vi tillämpade en serie Gauss-Transformationsändringar, kan vi göra detsamma och utföra en serie Hushållstransformationer
- så om vi väljer $y = \pm e_1$ (där $e_1$ är matrisen med 1 på position 1 och resten är nollor)
- då kommer det att nollställa alla element på $x$ utom den första
- således genom lämpligt val av $H$ kan vi ta $A$ och noll alla Subdiagonala element
- kan göra det flera gånger för varje kolumn på $A$
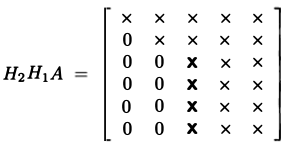
på så sätt kan vi utföra QR-sönderdelning:
Hessenberg-sönderdelning
istället för att använda den för att reducera matrisen till triangulär kan vi använda Hushållstransformation för att minska en matris till Hessenberg-matris