Algoritmo Codicioso con Ejemplos: Método y Enfoque Codicioso

Para entender el enfoque codicioso, necesitará tener un conocimiento práctico de recursión y cambio de contexto. Esto le ayuda a entender cómo rastrear el código. Puedes definir el paradigma codicioso en términos de tus propias declaraciones necesarias y suficientes.

Dos condiciones definen el paradigma codicioso.

• Cada solución escalonada debe estructurar un problema hacia su solución mejor aceptada.
• Es suficiente si la estructuración del problema puede detenerse en un número finito de pasos codiciosos.

Con la teorización continuada, describamos la historia asociada con el enfoque de búsqueda Codicioso.

En este tutorial de algoritmo codicioso, aprenderás:

• Historia de Algoritmos Codiciosos
• Estrategias y Decisiones Codiciosas
• Características del Enfoque Codicioso
• ¿Por qué usar el Enfoque Codicioso?
• Cómo resolver el problema de selección de actividades
• Arquitectura del enfoque Codicioso
• Desventajas de los algoritmos Codiciosos

Historia de los algoritmos Codiciosos

Aquí hay un hito importante de los algoritmos codiciosos:

• Los algoritmos codiciosos se conceptualizaron para muchos algoritmos de caminata de gráficos en la década de 1950.
• Esdger Djikstra conceptualizó el algoritmo para generar árboles de expansión mínimos. Su objetivo era acortar el alcance de las rutas dentro de la capital holandesa, Ámsterdam.
• En la misma década, Prim y Kruskal lograron estrategias de optimización que se basaban en minimizar los costos de la ruta a lo largo de las rutas pesadas.
• En los años 70, investigadores estadounidenses, Cormen, Rivest y Stein propusieron una subestructura recursiva de soluciones codiciosas en su libro de introducción clásica a los algoritmos.
• El paradigma de búsqueda Codiciosa se registró como un tipo diferente de estrategia de optimización en los registros del NIST en 2005.
• Hasta la fecha, los protocolos que ejecutan la web, como el open-shortest-path-first (OSPF) y muchos otros protocolos de conmutación de paquetes de red, utilizan la estrategia codiciosa para minimizar el tiempo invertido en una red.

Estrategias y decisiones codiciosas

La lógica en su forma más fácil se redujo a «codiciosa» o «no codiciosa». Estas declaraciones fueron definidas por el enfoque adoptado para avanzar en cada etapa del algoritmo.

Por ejemplo, el algoritmo de Djikstra utilizó una estrategia codiciosa por pasos para identificar hosts en Internet mediante el cálculo de una función de costo. El valor devuelto por la función de coste determina si la siguiente ruta es «codiciosa» o «no codiciosa».

En resumen, un algoritmo deja de ser codicioso si en cualquier etapa da un paso que no es codicioso localmente. Los problemas codiciosos se detienen sin más alcance de codicia.

Características del enfoque Codicioso

Las características importantes de un algoritmo de método codicioso son:

• Hay una lista ordenada de recursos, con costos o atribuciones de valor. Estos cuantifican las limitaciones de un sistema.
• Tomará la cantidad máxima de recursos en el tiempo que se aplique una restricción.
• Por ejemplo, en un problema de programación de actividades, los costos de recursos se expresan en horas y las actividades deben realizarse en orden serial.

¿Por qué usar el Enfoque Codicioso?

Aquí están las razones para usar el enfoque codicioso:

• El enfoque codicioso tiene algunas compensaciones, lo que puede hacerlo adecuado para la optimización.
• Una razón importante es lograr la solución más factible de inmediato. En el problema de selección de actividades (explicado a continuación), si se pueden realizar más actividades antes de terminar la actividad actual, estas actividades se pueden realizar al mismo tiempo.
• Otra razón es dividir un problema recursivamente en función de una condición, sin necesidad de combinar todas las soluciones.
• En el problema de selección de actividades, el paso de «división recursiva» se logra escaneando una lista de elementos una sola vez y considerando ciertas actividades.

Cómo resolver el problema de selección de actividades

En el ejemplo de programación de actividades, hay un tiempo de «inicio» y «finalización» para cada actividad. Cada actividad está indexada por un número de referencia. Hay dos categorías de actividades.

1. actividad considerada: es la Actividad, que es la referencia a partir de la cual se analiza la capacidad de hacer más de una Actividad restante.
2. actividades restantes: actividades en uno o más índices por delante de la actividad considerada.

La duración total da el costo de realizar la actividad. Es decir, (finish-start) nos da la duración como el costo de una actividad.

Aprenderá que la extensión codiciosa es el número de actividades restantes que puede realizar en el tiempo de una actividad considerada.

Arquitectura del enfoque Codicioso

PASO 1)

Escanee la lista de costos de actividad, comenzando con el índice 0 como el índice considerado.

PASO 2)

Cuando se puedan terminar más actividades en el momento en que finalice la actividad considerada, comience a buscar una o más actividades restantes.

PASO 3)

Si no hay más actividades restantes, la actividad restante actual se convierte en la siguiente actividad considerada. Repita el paso 1 y el paso 2, con la nueva actividad considerada. Si no quedan actividades, vaya al paso 4.

PASO 4)

Devuelve la unión de los índices considerados. Estos son los índices de actividad que se utilizarán para maximizar el rendimiento.

Explicación del Código

#include<iostream>#include<stdio.h>#include<stdlib.h>#define MAX_ACTIVITIES 12

Explicación del código:

1. Archivos/clases de encabezado incluidos
2. Un número máximo de actividades proporcionadas por el usuario.

using namespace std;class TIME{ public: int hours; public: TIME() { hours = 0; }};

Explicación del código:

1. El espacio de nombres para las operaciones de streaming.
2. Una definición de clase para el TIEMPO
3. Una marca de tiempo de hora.
4. Un constructor de TIEMPO predeterminado
5. La variable horas.

class Activity{ public: int index; TIME start; TIME finish; public: Activity() { start = finish = TIME(); }};

Explicación del código:

1. Una definición de clase de activity
2. Marcas de tiempo que definen una duración
3. Todas las marcas de tiempo se inicializan a 0 en el constructor predeterminado

class Scheduler{ public: int considered_index,init_index; Activity *current_activities = new Activity; Activity *scheduled;

Explicación del código:

1. Parte 1 de la definición de la clase scheduler.
2. El índice considerado es el punto de partida para escanear la matriz.
3. El índice de inicialización se utiliza para asignar marcas de tiempo aleatorias.
4. Una matriz de objetos de actividad se asigna dinámicamente utilizando el nuevo operador.
5. El puntero programado define la ubicación base actual de greed.

Scheduler(){ considered_index = 0; scheduled = NULL;......

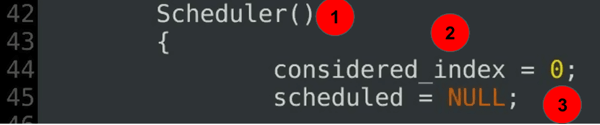
Explicación del código:

1. El constructor del planificador-parte 2 de la definición de la clase del planificador.
2. El índice considerado define el inicio actual del análisis actual.
3. La extensión codiciosa actual no está definida al principio.

for(init_index = 0; init_index < MAX_ACTIVITIES; init_index++) { current_activities.start.hours = rand() % 12; current_activities.finish.hours = current_activities.start.hours + (rand() % 2); printf("\nSTART:%d END %d\n", current_activities.start.hours ,current_activities.finish.hours); }……

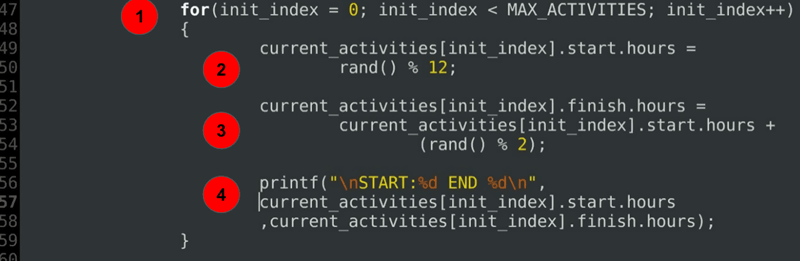
Explicación del código:

1. Un bucle for para inicializar las horas de inicio y finalización de cada una de las actividades programadas actualmente.
2. Inicialización de la hora de inicio.
3. Inicialización de la hora de finalización siempre después o exactamente a la hora de inicio.
4. Una instrucción de depuración para imprimir las duraciones asignadas.

public: Activity * activity_select(int);};

Explicación del código:

1. Parte 4 – la última parte de la definición de la clase scheduler.
2. La función de selección de actividad toma un índice de punto de partida como base y divide la misión codiciosa en subproblemas codiciosos.

Activity * Scheduler :: activity_select(int considered_index){ this->considered_index = considered_index; int greedy_extent = this->considered_index + 1;…… 

1. Utilizando el operador de resolución de alcance (::), se proporciona la definición de la función.
2. El Índice considerado es el Índice llamado por valor. El greedy_extent es el índice inicializado después del Índice considerado.

Activity * Scheduler :: activity_select(int considered_index){ while( (greedy_extent < MAX_ACTIVITIES ) && ((this->current_activities).start.hours < (this->current_activities).finish.hours )) { printf("\nSchedule start:%d \nfinish%d\n activity:%d\n", (this->current_activities).start.hours, (this->current_activities).finish.hours, greedy_extent + 1); greedy_extent++; }…...

Explicación del código:

1. La lógica central – El alcance codicioso se limita al número de actividades.
2. Las horas de inicio de la Actividad actual se comprueban como programables antes de que finalice la Actividad considerada (dada por índice considerado).
3. Siempre que sea posible, se imprime una instrucción de depuración opcional.
4. Avanzar al siguiente índice en la matriz de actividades

...if ( greedy_extent <= MAX_ACTIVITIES ) { return activity_select(greedy_extent); } else { return NULL; }}

Explicación del código:

1. Las comprobaciones condicionales si se han cubierto todas las actividades.
2. Si no, puede reiniciar su codicioso con el Índice considerado como el punto actual. Este es un paso recursivo que divide con avidez la declaración del problema.
3. En caso afirmativo, se devuelve al llamante sin margen para extender la codicia.

int main(){ Scheduler *activity_sched = new Scheduler(); activity_sched->scheduled = activity_sched->activity_select( activity_sched->considered_index); return 0;}

Explicación del código:

1. La función principal utilizada para invocar el planificador.
2. Se crea una instancia de un nuevo Programador.
3. La función activity select, que devuelve un puntero de tipo activity, vuelve a la persona que llama una vez finalizada la búsqueda codiciosa.

Salida:

START:7 END 7START:9 END 10START:5 END 6START:10 END 10START:9 END 10Schedule start:5 finish6 activity:3Schedule start:9 finish10 activity:5

Desventajas de los algoritmos Codiciosos

No es adecuado para problemas Codiciosos donde se requiere una solución para cada subproblema como la clasificación.

En tales problemas de práctica de algoritmos Codiciosos, el método Codicioso puede ser incorrecto; en el peor de los casos, incluso puede conducir a una solución no óptima.

Por lo tanto, la desventaja de los algoritmos codiciosos es no saber lo que está por delante del estado codicioso actual.

A continuación se muestra una descripción de la desventaja del método Codicioso:

En el escaneo codicioso que se muestra aquí como un árbol (valor más alto, mayor codicia), un estado de algoritmo en el valor: 40, es probable que tome 29 como el siguiente valor. Además, su misión termina en 12. Esto equivale a un valor de 41.

Sin embargo, si el algoritmo tomó un camino subóptimo o adoptó una estrategia de conquista. luego, 25 serían seguidos por 40, y la mejora de costos general sería de 65, lo que se valora 24 puntos más como una decisión subóptima.

Ejemplos de algoritmos Codiciosos

La mayoría de los algoritmos de red utilizan el enfoque codicioso. Aquí hay una lista de algunos ejemplos de algoritmos codiciosos:

• Algoritmo de Árbol de Expansión Mínima de Prim
• Problema de Vendedor Ambulante
• Coloración de Mapa de Gráficos
• Algoritmo de Árbol de Expansión Mínima de Kruskal
• Algoritmo de Árbol de Expansión Mínima de Dijkstra
• Cubierta de Vértices de Gráficos
• Problema de mochila
• Problema de programación de trabajos

Resumen:

En resumen, el artículo definió el paradigma codicioso, mostró cómo la optimización codiciosa y la recursión pueden ayudarlo a obtener la mejor solución hasta cierto punto. El algoritmo Greedy es ampliamente utilizado para la resolución de problemas en muchos lenguajes como el algoritmo Greedy Python, C, C#, PHP, Java, etc. El ejemplo de selección de actividad del algoritmo Greedy se describió como un problema estratégico que podría lograr el máximo rendimiento utilizando el enfoque greedy. Al final, se explicaron los deméritos del uso del enfoque codicioso.