CONDUCTIVIDAD TÉRMICA

La conductividad térmica de los sólidos es de naturaleza diferente dependiendo de si son conductores o no. En los dieléctricos sin cargas eléctricas libres, la energía térmica es transferida por fonones. Las vibraciones colectivas de los átomos en la red cristalina toman la forma de ondas de desplazamiento, cuya interferencia genera paquetes de ondas, es decir, fonones. Las ondas de desplazamiento producen fluctuaciones de densidad que pueden manifestarse como una variación del índice de refracción. Si las ondas pasan a través de una región en la que el índice de refracción difiere del valor volumétrico medio, las ondas de desplazamiento posteriores que transportan la energía del movimiento térmico se dispersarán.

La dispersión es más fuerte, mayor es la desviación máxima de los átomos de sus posiciones medias en la red, es decir, mayor es la T. Esto explica el hecho establecido experimentalmente de que la conductividad térmica de los dieléctricos de cristal disminuye a temperaturas bastante altas: λ 1 / T (Figura 1).

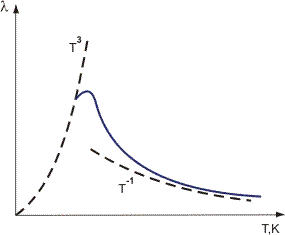
Figura 1. Variación de la conductividad térmica de los dieléctricos de cristal con la temperatura.

Debye dio una idea de un carácter de pico de variación λ (T) a T baja dentro del marco de los conceptos de la mecánica cuántica. Elaboró una teoría dipolar de dieléctricos basada en el concepto de una molécula como dipolo rígido. En este modelo, Debye introdujo el concepto de la llamada temperatura de Debye θD proporcional a la frecuencia máxima de vibraciones atómicas en un sólido. Para la mayoría de las sustancias, θD es inferior o cercana a la temperatura ambiente (una excepción es el diamante para el que θD = 1850 K y el berrylium para el que θD = 1160 K).

En la teoría cuántica de sólidos, la red cristalina se considera como un volumen lleno de gas fonónico al que se aplica la deducción de la teoría cinética más simple

donde c es la capacidad calorífica de un dieléctrico que coincide con la del gas fonón, v la velocidad media de los fonones aproximadamente igual a la velocidad del sonido,la trayectoria libre media de los fonones. La existencia de un cierto valor finito de es el resultado de la dispersión de fonones en fonones, en defectos de la red cristalina y, en particular, en los límites de grano sobre toda la muestra. La dependencia de temperatura λ (T) está determinada por la dey c de la temperatura.

A altas temperaturas que exceden sustancialmente la temperatura de Debye θD, el mecanismo básico que limita es una dispersión fonón-fonón debido a la anarmonía de las vibraciones atómicas en un cristal. El mecanismo fonón-fonón de resistencia térmica ((1 / λ) se conoce como coeficiente de resistencia térmica) es factible solo debido a una transición que resulta en un retraso del flujo fonónico y un cambio apreciable del cuasi-momento. Cuanto mayor sea la T, mayor será la probabilidad de la transición con decreciente:(1/T). Dado que en T > θD la capacidad calorífica c solo aumenta ligeramente con la temperatura, por lo tanto, λ1/T.

A temperaturas inferiores a la temperatura de Debye, T< < θD, la longitud de la trayectoria libre mediadeterminada por la dispersión fonón-fonón crece drásticamente, expθD / T y, por regla general, se limita al tamaño de un cristal R. De acuerdo con la ley de Debye, la capacidad de calor c en este rango de temperatura varía como c(T/θD)3. En consecuencia, en T → 0, el coeficiente de conductividad térmica λ debe disminuir en proporción a T3. La temperatura para la que la conductividad térmica tiene un pico se determina a partir de≈ R, que comúnmente corresponde a T ≤ 0.05 θD.

Esta teoría también explica el comportamiento del coeficiente de conductividad térmica para sustancias amorfas que no tienen un orden de largo alcance, es decir, el tamaño de sus «cristales» es del orden de los tamaños atómicos. En virtud de esto, la dispersión en los «límites» de estas sustancias debe prevalecer en todos los T y≈ const. Coeficiente de conductividad térmica de sustancias amorfas λT3 a bajas temperaturas y debe crecer ligeramente, en proporción a la capacidad calorífica, a temperaturas moderadas y altas, T > θD.

Todo esto proporciona una explicación cualitativa de la dependencia λ (T) en dieléctricos cristalinos reales, pero no tiene en cuenta las desviaciones de la red constante debido a las impurezas atómicas de otros elementos y sus propios isótopos. A altas temperaturas, la resistencia que ofrecen las impurezas al transporte de calor es independiente de la temperatura. Esto permite estimar el grado de pureza del cristal a partir de la variación de su conductividad térmica con la temperatura. El mismo hecho nos permite determinar la distribución entre la sustancia vítrea y cristalina en el mineral natural si el vidrio se considera una impureza en un cristal.

La conductividad térmica en metales depende del movimiento y la interacción de los portadores de corriente, es decir, los electrones de conducción. Generalmente, el coeficiente de conductividad térmica λ de un metal es igual a la suma de la red (fonón) λph, y los componentes λe de electrones, λ = λe + λph; a temperaturas ordinarias, como regla general, λe >>λph.

Si aplicamos una teoría cinética simple de gases al flujo de electrones libres y asumimos que la longitud de su trayectoria libre no depende de la velocidad, entonces la teoría implica que

donde e es la carga de electrones, K la constante de Boltzrnann y σ la conductividad eléctrica. Una teoría mecánica cuántica estricta ofrece una relación similar,

En ambas fórmulas, la relación de la parte electrónica del coeficiente de conductividad térmica λ a la conductividad eléctrica σ, en un amplio rango de temperaturas, parece ser proporcional a la temperatura de acuerdo con la ley de Wiedemann-Franz, λ/σ = LT, donde L es el número de Lorentz. Esta ley se utiliza para calcular λe a partir de la conductividad eléctrica medida. Sin embargo, se viola a temperaturas por debajo de θD cuando prevalece una interacción electrón-fonón (σ crece con T decreciente como T−5, mientras que le varía más ligeramente como T−2).

Los hallazgos experimentales demuestran que, por regla general, la conductividad térmica de los metales a altas temperaturas es una función ligeramente decreciente de la temperatura. Pero hay muchas excepciones. Por lo tanto, la conductividad térmica del hierro disminuye fuertemente con la temperatura, mientras que el tántalo y el niobio muestran un coeficiente de temperatura positivo.

De interés son los intentos de comparar los coeficientes de conductividad térmica para diferentes sustancias para una sola temperatura característica, por ejemplo, para el punto de fusión Tm de sólidos. Por lo tanto, el procesamiento estadístico de datos experimentales llevado a cabo por Missenard ha demostrado que la conductividad térmica de los metales en el punto de fusión λ(T = Tm) = λm es proporcional a λy la conductividad térmica de los cristales dieléctricos en T = Tm es proporcional a, donde m es la masa molecular, N el número de átomos en la fórmula química, ρ la densidad y el punto de fusión Tm está en Kelvin.

El transporte de calor en semiconductores es más complejo que en dieléctricos y metales porque los componentes fonón y electrón son igualmente esenciales para ellos. Otra razón de la complejidad es el considerable efecto de las impurezas, la difusión bipolar y otros factores poco estudiados en la transferencia de calor.

El efecto de la presión sobre la conductividad térmica de sólidos se puede suponer, con una buena precisión, que es lineal, λ para muchos metales que crecen con p.

Para el efecto de la porosidad sobre la conductividad térmica de sólidos, véase Medio poroso.