Pokud jste si přečetli předchozí příspěvek o tom, co je induktor, pojďme pokračovat na další úroveň, jaká je indukčnost vzorce obvodů.
Nyní, když byl induktor přidán do našeho seznamu pasivních prvků, je nutné rozšířit výkonný nástroj sériové paralelní kombinace. Musíme vědět, jak najít ekvivalentní indukčnost sériově připojené nebo paralelně připojené sady induktorů nalezené v praktických obvodech.
sériové induktory
zvažte sériové připojení n induktorů, jak je znázorněno na obrázku.(1a), s rovnocenným obvodem znázorněným na obrázku.(1b).

induktory mají přes ně stejný proud. Použití KVL do smyčky,

Dosazením vk= Lk di/dt výsledky v
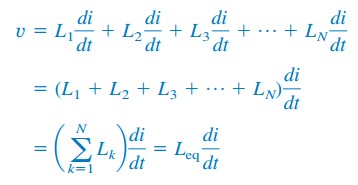
kde

Tak,
ekvivalentní indukčnosti sériově připojené tlumivky je součet jednotlivých indukčností.
induktory v sérii jsou kombinovány přesně stejným způsobem jako rezistory v sérii.
paralelní induktory
nyní uvažujeme paralelní připojení n induktorů, jak je znázorněno na obrázku.(2a), s rovnocenným obvodem na obrázku.(2b). Induktory mají na sobě stejné napětí. Pomocí KCL,

Ale


proto

kde
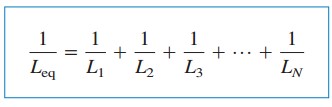
počáteční proud i(t0) prostřednictvím Leq t= t0 se očekává KCL být součet induktor proudů v čase t0. Tedy podle rovnice.(5),
![]()
Podle Rovnice.(6),
ekvivalentní indukčnost paralelní tlumivky je převrácená hodnota součtu převrácené hodnoty jednotlivých indukčností.
Všimněte si, že induktory paralelně jsou kombinovány stejným způsobem jako odpory paralelně.
pro dva induktory paralelně (N = 2), rovnice.(6) stává
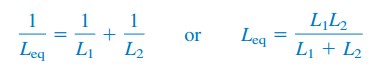
Indukčnosti Vzorec Obvody Příklady
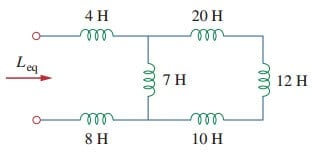
1. Najděte ekvivalentní indukčnost obvodu znázorněného na obrázku.(3).
Řešení:
10 H, 12 H, a 20-H tlumivky do série; tím, že kombinuje jim dává 42-H indukčnost. Tento 42-H induktor je souběžně s 7-H cívky tak, že jsou kombinovány, aby


6-H induktor v sérii s 4-H a 8-H induktory. Proto,
![]()
2. Pro obvod na obrázku.(4),
i (t) = 4 (2 − e−10t) mA. Pokud i2 (0) = -1 mA, najděte:
(a) i1 (0);
(b) v(t), v1(t) a v2(t);
(c) i1(t) a i2(t).

Řešení:
() Z i(t) = 4(2 − e−10t) mami, já(0) = 4(2 − 1) = 4 mA.
Since i = i1 + i2,
![]()
(b) The equivalent inductance is
![]()
Thus,


and


Since v = v1 + v2,
![]()
(c) proud i1 je získaná jako


Podobně,


Všimněte si, že i1(t) + i2(t) = i(t).