Jednoduché Ornstein-Uhlenbeck Modely

Odhad Evoluční Optima

Tento výukový program ukazuje, jak určit, Ornstein-Uhlenbeck model, kde optimální fenotyp se předpokládá konstantní mezi větve časově kalibrovaná fylogeneze (chybějící odkaz) pomocí datových souborů (log) tělo-velikost přes obratlovců clades (chybějící odkaz). Pro tento tutoriál poskytujeme pravděpodobnostní grafické znázornění jednotlivých komponent. Po zadání modelu odhadnete parametry Ornstein-Uhlenbeck evolution pomocí Markovova řetězce Monte Carlo (MCMC).

Ornstein-Uhlenbeck Model

Pod jednoduché Ornstein-Uhlenbeck (OU) model, kontinuální charakter, předpokládá se vyvíjet směrem k optimální hodnotě, $\theta$. Znak se vyvíjí stochasticky podle driftového parametru $ \ sigma^2$. Postava je tažena směrem k optimu rychlostí adaptace, $ \ alpha$; větší hodnoty alfa naznačují, že znak je tažen silněji směrem k $\theta$. Jak se znak pohybuje od $\theta$, parametr $ \ alpha$ určuje, jak silně je znak stažen zpět. Z tohoto důvodu je $ \ alpha$ někdy označován jako parametr „gumička“. Když rychlost adaptačního parametru $ \ alpha = 0$, model OU se zhroutí na model BM. Výsledný grafický model je poměrně jednoduchý, protože pravděpodobnost spojitých znaků závisí pouze na fylogenezi (kterou předpokládáme v tomto tutoriálu) a parametru three ou ().

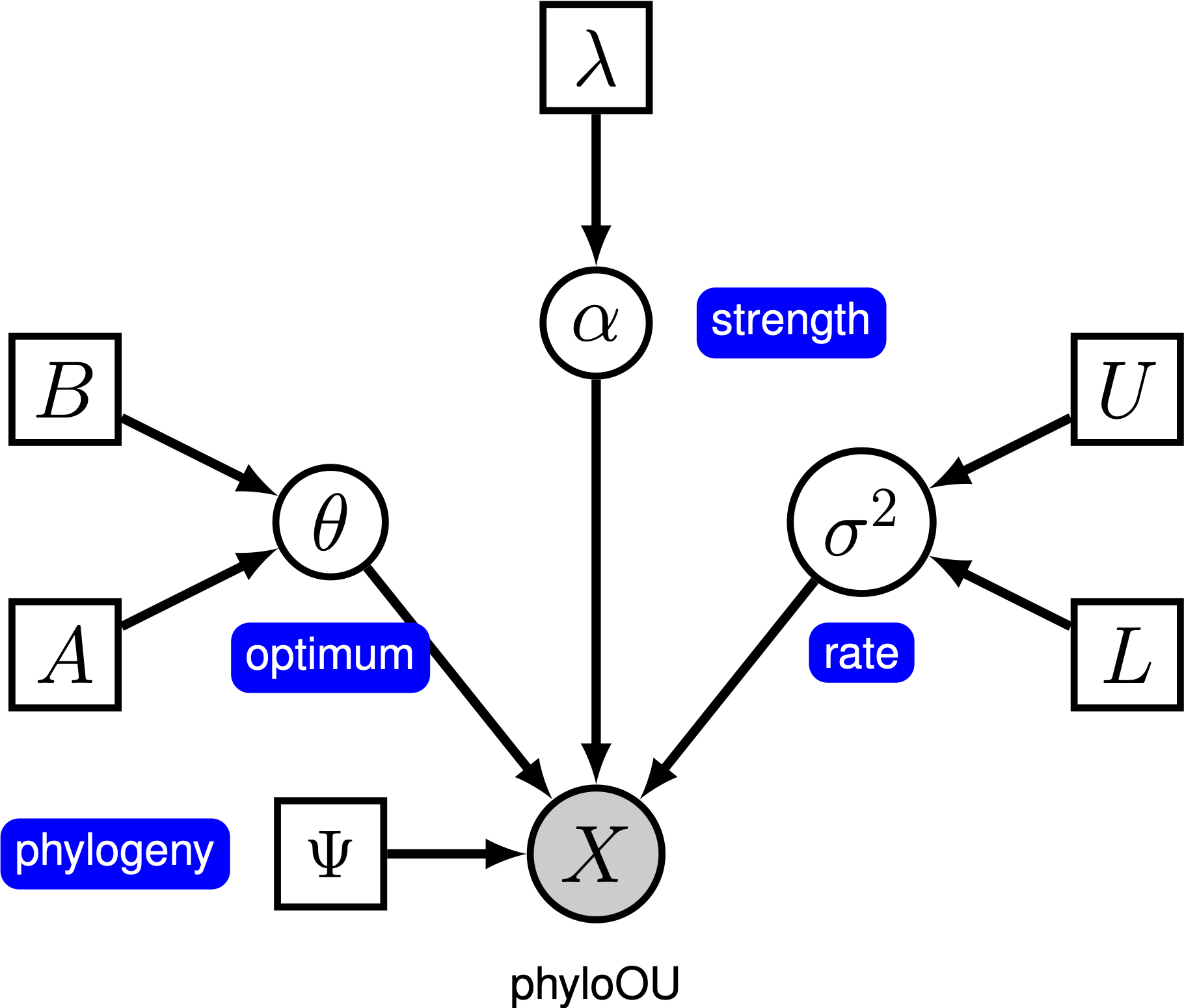
v tomto tutoriálu používáme 66 fylogenií obratlovců a (log) datových souborů velikosti těla z (Landis and Schraiber 2017).

⇨ úplná specifikace OU-modelu je v souboru nazvaném mcmc_OU.Rev.

Přečtěte si data

začneme rozhodnutím, který z 66 datových souborů obratlovců použít. Zde předpokládáme, že analyzujeme první datovou sadu (Acanthuridae), ale měli byste si vybrat libovolnou datovou sadu.

dataset <- 1

nyní čteme ve stromu (časově kalibrovaném) odpovídajícím našemu vybranému datovému souboru.

T <- readTrees("data/trees.nex")

dále čteme v znakových datech pro stejnou datovou sadu.

data <- readContinuousCharacterData("data/traits.nex")

dále inicializujeme proměnnou pro náš vector ofmoves a monitory:

moves = VectorMoves()monitors = VectorMonitors()

s Uvedením modelu

Strom modelu

V tomto tutoriálu, budeme předpokládat, že strom je známý, aniž oblasti. Pro strom vytvoříme konstantní uzel, který odpovídá pozorované fylogenezi.

tree <- T

parametr rychlosti

stochastická rychlost evoluce je řízena parametrem rychlosti, $ \ sigma^2$. Parametr rychlosti čerpáme z loguniform prior. Tento prior je jednotný na stupnici log, což znamená, že představuje neznalost o řádovém rozsahu sazby.

sigma2 ~ dnLoguniform(1e-3, 1)

abychom mohli odhadnout zadní rozdělení $ \ sigma^2$, musíme poskytnout mechanismus návrhu MCMC, který pracuje na tomto uzlu. Protože $ \ sigma^2$ je parametr míry, a proto musí být kladný, použijeme tah měřítka nazvaný mvScale.

moves.append( mvScale(sigma2, weight=1.0) )

Adaptace parametr

míra adaptace k optimální je určena parametrem $\alpha$. Nakreslíme $ \ alpha$ z exponenciálního předchozího rozdělení a umístíme na něj návrh měřítka.

alpha ~ dnExponential(10)moves.append( mvScale(alpha, weight=1.0) )

Optimální

nakreslíme optimální hodnotu z vágní uniformě před v rozmezí od -10 do 10 (měli byste změnit to předchozí, pokud vaše postava je mimo tento rozsah). Protože tento parametr může být kladný nebo záporný, použijeme posuvný pohyb k návrhu změn během MCMC.

theta ~ dnUniform(-10, 10)moves.append( mvSlide(theta, weight=1.0) )

Ornstein-Uhlenbeck model

Teď, že jsme určili parametry modelu, můžeme vyvodit charakter dat z příslušné fylogenetické OU model. V tomto příkladu používáme algoritmus REML k efektivnímu výpočtu pravděpodobnosti (Felsenstein 1985). Předpokládáme, že znak začíná na optimální hodnotě u kořene stromu.

X ~ dnPhyloOrnsteinUhlenbeckREML(tree, alpha, theta, sigma2^0.5, rootStates=theta)

Upozorňuje, že $X$ je pozorovaná data (), jsme svorka data tento stochastický uzel.

X.clamp(data)

nakonec vytvoříme objekt pracovního prostoru pro celý model s model(). Pamatujte, že objekty pracovního prostoru jsou inicializovány operátorem = a nejsou samy o sobě součástí Bayesovského grafického modelu. Funkce model() prochází celým grafem modelu a najde všechny uzly v modelu, který jsme zadali. Tento objekt poskytuje pohodlný způsob, jak odkazovat na celý objekt modelu, spíše než jen jeden uzel DAG.

mymodel = model(theta)

Běží MCMC analýzy

Upřesňující Monitory

Pro naše MCMC analýzy, musíme nastavit vektor monitory pro záznam státy naší Markovovy řetězce. Všechny funkce monitoru se nazývají mn*, kde * je zástupný znak představující typ monitoru. Nejprve inicializujeme modelový monitor pomocí funkce mnModel. Tím se vytvoří nová proměnná monitoru, která po předání do funkce MCMC vypíše stavy pro všechny parametry modelu.

monitors.append( mnModel(filename="output/simple_OU.log", printgen=10) )

navíc vytvořte monitor obrazovky, který bude hlásit stavy specifikovaných proměnných na obrazovku s mnScreen:

monitors.append( mnScreen(printgen=1000, sigma2, alpha, theta) )

Inicializace a spuštění MCMC Simulace

S plně specifikovaného modelu, sadu monitorů, a sadu pohybů, můžeme nyní nastavit MCMC algoritmus, který bude vzorek parametr hodnoty inproportion jejich posteriorní pravděpodobnosti. mcmc() funkce willcreate naše MCMC objekt:

mymcmc = mcmc(mymodel, monitors, moves, nruns=2, combine="mixed")

Nyní, spusťte MCMC:

mymcmc.run(generations=50000)

Když je analýza je kompletní, budete mít sledovaných souborů v youroutput firem.

⇨ soubor Rev pro provedení této analýzy: mcmc_OU.Rev

znaky vyvíjející se v rámci procesu OU budou mít tendenci ke stacionárnímu rozdělení, což je normální rozdělení s průměrem $\theta$ a rozptylem $ \ sigma^2 \div 2 \ alpha$. Proto, pokud jsou míry evoluce vysoké (nebo větve ve stromu jsou relativně dlouhé), může být obtížné odhadnout $\sigma^2$ a $\alpha$ samostatně, protože oba určují dlouhodobý rozptyl procesu. Můžeme vidět, zda to ovlivňuje naši analýzu zkoumáním společného zadního rozdělení parametrů v Tracer. Když parametry jsou pozitivně korelované, měli bychom váhat a interpretovat jejich marginální rozdělení (tj., ne dělat závěry o míře adaptace, nebo rozptyl parametrů samostatně).

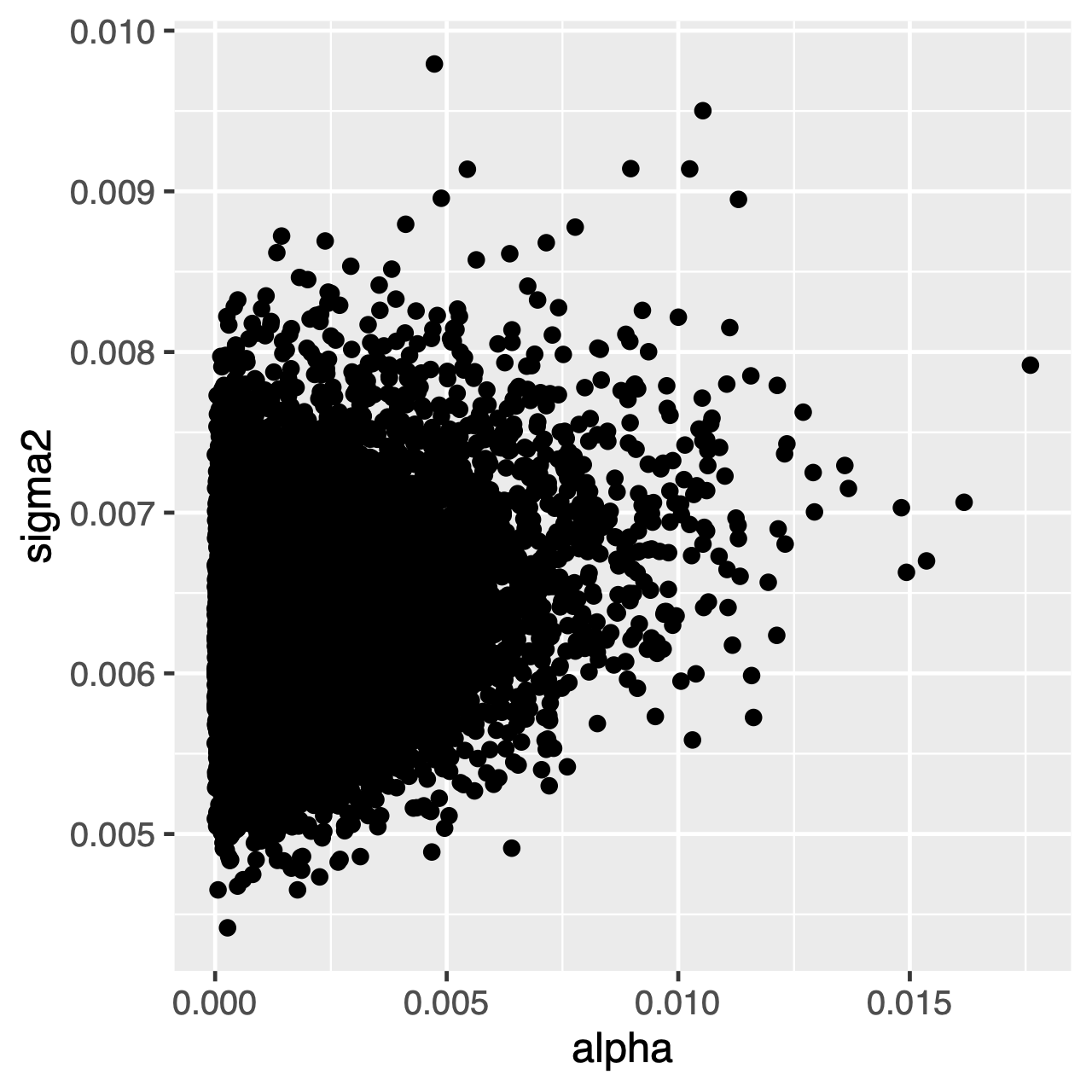
cvičení 1

• spusťte simulaci MCMC, abyste odhadli zadní rozdělení ou optimum (theta).
• načtěte vygenerovaný výstupní soubor do Tracer: jaký je střední Zadní odhad theta a jaký je odhadovaný HPD?
• použijte Tracer k porovnání kloubních zadních distribucí alpha a sigma2. Jsou tyto parametry korelované nebo nekorelované?
• Porovnejte předchozí průměr se zadním průměrem. (TIP: Použijte volitelný argument underPrior=TRUE ve funkci mymcmc.run()) liší se (např. )? Je zadní průměr mimo předchozí 95% interval pravděpodobnosti?

porovnání modelů OU a BM

Nyní, když se můžeme vejít do modelů BM i OU, můžeme přirozeně chtít vědět, který model se hodí lépe. V této části se naučíme, jak použít reverzibilní Markovův řetěz Monte Carlo k porovnání fit modelů OU a BM.

Výběr Modelu pomocí Reverzibilní-Skok MCMC

testovat hypotézu, že postava se vyvíjí směrem k selektivní optimální, jsme si představit dva modely. První model, kde neexistuje žádná adaptace na optimální,je případ, kdy $ \ alpha = 0$. Druhý model odpovídá modelu OU s $ \ alpha > 0$. Funguje to proto, že Brownianův pohyb je zvláštním případem modelu OU, když je rychlost adaptace 0. Bohužel, protože $ \ alpha$ je spojitý parametr, standardní Markovův řetězec nikdy nenavštíví stavy, kde je každá hodnota přesně rovna 0. Naštěstí můžeme použít reverzibilní skok, který umožní řetězci Markov zvážit návštěvu modelu Brownian-motion. To zahrnuje určení předchozí pravděpodobnosti u každého ze dvou modelů a poskytnutí předchozí distribuce pro $ \ alpha$ pro model OU.

použití rjMCMC umožňuje řetězci Markov navštívit dva modely v poměru k jejich zadní pravděpodobnosti. Zadní pravděpodobnost modelu $I$ je jednoduše zlomek vzorků, kde řetězec navštěvoval tento model. Protože jsme také zadat před na modely, můžeme vypočítat Bayesův Faktor pro OU model jako:

\

kde $P( \text{OU model} \mid X)$ a $P( \text{OU model})$ jsou posteriorní pravděpodobnosti a předchozí pravděpodobnost OU model, respektive.

Reverzibilní-skok mezi OU a BM modely

povolit rjMCMC, my prostě muset umístit reverzibilní-skok před na příslušný parametr, $\alpha$. Můžeme upravit Prioru na alpha tak, že trvá buď konstantní hodnota 0, nebo je čerpána z předchozího rozdělení. Nakonec specifikujeme předchozí Pravděpodobnost na OU modelu p = 0.5.

alpha ~ dnReversibleJumpMixture(0.0, dnExponential(10), 0.5)

poté poskytneme návrh reverzibilního skoku na alpha, který navrhuje změny mezi oběma modely.

moves.append( mvRJSwitch(alpha, weight=1.0) )

dále poskytujeme normální mvScale návrh, kdy MCMC navštěvuje model OU.

moves.append( mvScale(alpha, weight=1.0) )

zahrnujeme proměnnou, která má hodnotu 1, když řetězec navštěvuje model OU, a odpovídající proměnnou, která má hodnotu 1, když navštěvuje model BM. To nám umožní snadno vypočítat zadní pravděpodobnost modelů, protože jednoduše potřebujeme vypočítat zadní střední hodnotu tohoto parametru.

is_OU := ifelse(alpha != 0.0, 1, 0)is_BM := ifelse(alpha == 0.0, 1, 0)

podíl vzorků, pro které is_OU = 1 je zadní pravděpodobnost modelu OU. Alternativně zadní střední odhad této indikátorové proměnné odpovídá zadní pravděpodobnosti modelu OU. Tyto hodnoty lze použít ve výše uvedené rovnici Bayesova faktoru pro výpočet podpory Bayesova faktoru pro oba modely.

1. Felsenstein J.1985. Fylogeneze a srovnávací metoda. Americký Přírodovědec.:1-15.10.1086/284325
2. Höhna S., Heath, T. A., Boussau B., Landis M. J., F. Ronquist, Huelsenbeck J. P. 2014. Pravděpodobnostní grafické znázornění modelu ve Fylogenetice. Systematická Biologie. 63:753-771.10.1093/sysbio/syu039
3. Landis M. J., Schraiber J. G. 2017. Pulzní evoluce formovala moderní velikosti těla obratlovců. Sborník Národní akademie věd. 114: 13224-13229. 10. 1073/pnas.1710920114