Simple Ornstein-Uhlenbeck modeller

estimering af evolutionær Optima

denne tutorial demonstrerer, hvordan man specificerer en Ornstein-Uhlenbeck-model, hvor den optimale fænotype antages at være konstant blandt grene af en tidskalibreret fylogeni (manglende reference) ved hjælp af datasættene for (log) kropsstørrelse på tværs af hvirveldyrsklader fra (manglende reference). Vi leverer den sandsynlige grafiske modelrepræsentation af hver komponent til denne tutorial. Når du har angivet modellen, estimerer du parametrene for Ornstein-Uhlenbeck evolution ved hjælp af Markov-kæden Monte Carlo (MCMC).

Ornstein-Uhlenbeck Model

under den enkle Ornstein-Uhlenbeck (OU) model antages en kontinuerlig karakter at udvikle sig mod en optimal værdi, $\theta$. Karakteren udvikler sig stokastisk i henhold til en driftsparameter, $\sigma^2$. Tegnet trækkes mod det optimale ved tilpasningshastigheden, $ \ alpha$; større værdier af alpha indikerer, at tegnet trækkes stærkere mod $\theta$. Når tegnet bevæger sig væk fra $\theta$, bestemmer parameteren $\alpha$, hvor stærkt tegnet trækkes tilbage. Af denne grund kaldes $\alpha$ undertiden som en” gummibånd ” – parameter. Når tilpasningsparameteren $ \ alpha = 0$, kollapser ou-modellen til BM-modellen. Den resulterende grafiske model er ret simpel, da sandsynligheden for de kontinuerlige tegn kun afhænger af fylogeni (som vi antager at være kendt i denne tutorial) og de tre ou-parametre ().

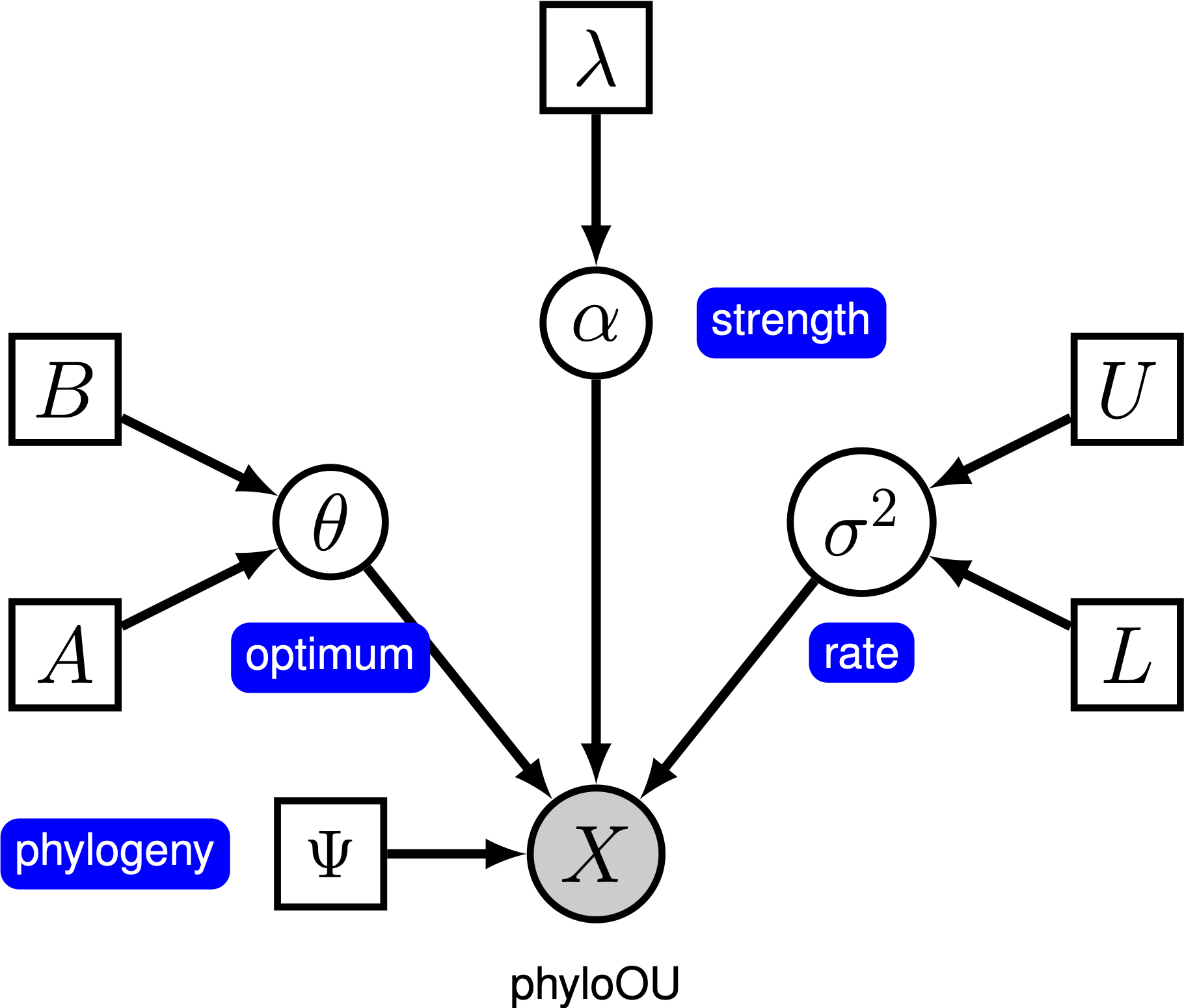
i denne tutorial bruger vi de 66 hvirveldyrsfylogenier og (log) kropsstørrelsesdatasæt fra (Landis and Schraiber 2017).

den fulde ou-model specifikation er i filen kaldet mcmc_OU.Rev.

Læs dataene

vi begynder med at beslutte, hvilke af de 66 hvirveldyr datasæt der skal bruges. Her antager vi, at vi analyserer det første datasæt (Acanthuridae), men du er velkommen til at vælge et af datasætene.

dataset <- 1

nu læser vi i det (tidskalibrerede) træ svarende til vores valgte datasæt.

T <- readTrees("data/trees.nex")

dernæst læser vi i tegndataene for det samme datasæt.

data <- readContinuousCharacterData("data/traits.nex")

derudover initialiserer vi en variabel til vores vektor af bevægelser og skærme:

moves = VectorMoves()monitors = VectorMonitors()

angivelse af modellen

træmodel

i denne vejledning antager vi, at træet er kendt uden område. Vi skaber en konstant knude for træet, der svarer til den observerede fylogeni.

tree <- T

Hastighedsparameter

den stokastiske udviklingshastighed styres af hastighedsparameteren, $\sigma^2$. Vi tegner satsparameteren fra en loguniform prior. Denne forudgående er ensartet på logskalaen, hvilket betyder, at den repræsenterer uvidenhed om størrelsesordenen af satsen.

sigma2 ~ dnLoguniform(1e-3, 1)

for at estimere den bageste fordeling af $\sigma^2$ skal vi tilvejebringe en MCMC-forslagsmekanisme, der fungerer på denne knude. Fordi $ \ sigma^2$ er en hastighedsparameter, og derfor skal være positiv, bruger vi et skaleringsbevægelse kaldet mvScale.

moves.append( mvScale(sigma2, weight=1.0) )

Tilpasningsparameter

tilpasningshastigheden mod det optimale bestemmes af parameteren $\alpha$. Vi trækker $ \ alpha$ fra en eksponentiel forudgående distribution og placerer et skalaforslag på det.

alpha ~ dnExponential(10)moves.append( mvScale(alpha, weight=1.0) )

optimal

vi tegner den optimale værdi fra en vag ensartet prior, der spænder fra -10 til 10 (du skal ændre denne prior, hvis din karakter er uden for dette interval). Da denne parameter kan være positiv eller negativ, bruger vi et diasbevægelse til at foreslå ændringer under MCMC.

theta ~ dnUniform(-10, 10)moves.append( mvSlide(theta, weight=1.0) )

Ornstein-Uhlenbeck model

nu hvor vi har angivet parametrene for modellen, kan vi tegne tegndataene fra den tilsvarende fylogenetiske ou-model. I dette eksempel bruger vi REML-algoritmen til effektivt at beregne sandsynligheden (Felsenstein 1985). Vi antager, at karakteren begynder med den optimale værdi ved træets rod.

X ~ dnPhyloOrnsteinUhlenbeckREML(tree, alpha, theta, sigma2^0.5, rootStates=theta)

Bemærk at $ $ er de observerede data (), vi klemmer data til denne stokastiske knude.

X.clamp(data)

endelig opretter vi et arbejdsområdeobjekt for hele modellen med model(). Husk, at arbejdsområdeobjekter initialiseres med operatøren = og ikke selv er en del af den bayesiske grafiske model. Funktionen model() krydser hele modelgrafen og finder alle knudepunkter i den model, vi har angivet. Dette objekt giver en bekvem måde at henvise til hele modelobjektet, snarere end blot en enkelt dag node.

mymodel = model(theta)

kører en MCMC-analyse

specificering af skærme

til vores MCMC-analyse er vi nødt til at oprette en vektor af skærme for at registrere tilstandene i Vores Markov-kæde. Skærmfunktionerne kaldes alle mn*, hvor * er jokertegnet, der repræsenterer skærmtypen. Først initialiserer vi modelmonitoren ved hjælp af funktionen mnModel. Dette skaber en ny skærmvariabel, der udsender tilstandene for alle modelparametre, når de overføres til en MCMC-funktion.

monitors.append( mnModel(filename="output/simple_OU.log", printgen=10) )

derudover skal du oprette en skærmskærm, der rapporterer tilstandene forspecificerede variabler til skærmen med mnScreen:

monitors.append( mnScreen(printgen=1000, sigma2, alpha, theta) )

initialisering og kørsel af MCMC-simuleringen

med en fuldt specificeret model, et sæt skærme og et sæt bevægelser, kan vi nu oprette MCMC-algoritmen, der vil prøve parameterværdier iproportion til deres bageste Sandsynlighed. Funktionen mcmc() vilskabe vores MCMC-objekt:

mymcmc = mcmc(mymodel, monitors, moves, nruns=2, combine="mixed")

Kør nu MCMC:

mymcmc.run(generations=50000)

når analysen er færdig, vil du have de overvågede filer i dinoutput mappe.

ret Rev fil til udførelse af denne analyse: mcmc_OU.Rev

tegn, der udvikler sig under OU-processen, vil have tendens til en stationær fordeling, som er en normalfordeling med gennemsnitlig $\theta$ og varians $\sigma^2 \div 2\alpha$. Derfor, hvis udviklingshastighederne er høje (eller grenene i træet er relativt lange), kan det være vanskeligt at estimere $\sigma^2$ og $\alpha$ separat, da de begge bestemmer procesens langsigtede varians. Vi kan se, om dette påvirker vores Analyse ved at undersøge den fælles posterior fordeling af parametrene i Tracer. Når parametrene er positivt korrelerede, bør vi tøve med at fortolke deres marginale fordelinger (dvs.ikke drage konklusioner om tilpasningshastigheden eller variansparameteren separat).

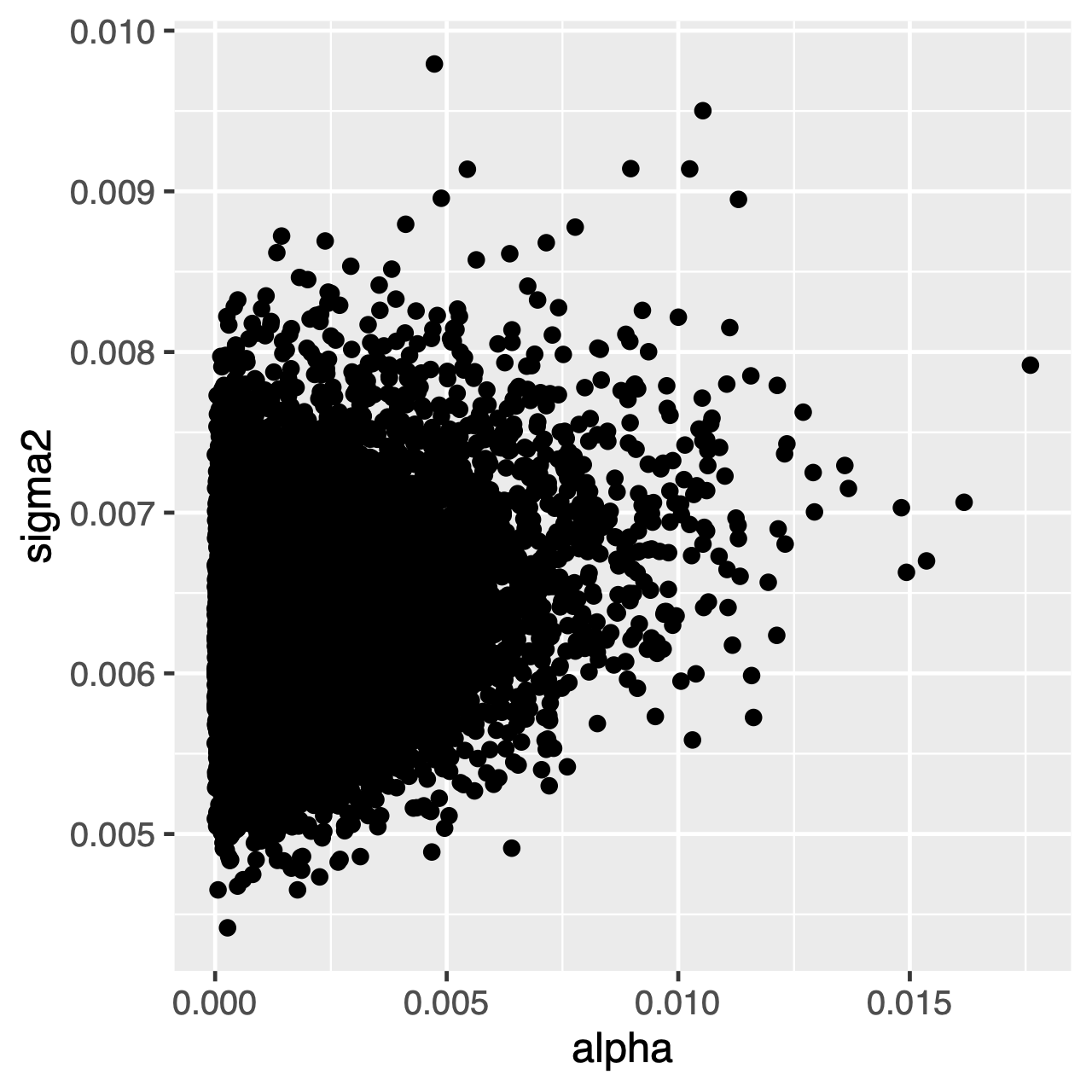
øvelse 1

• Kør en MCMC-simulering for at estimere den bageste fordeling af ou optimum (theta).
• indlæs den genererede outputfil i Tracer: Hvad er det gennemsnitlige bageste skøn over theta, og hvad er den estimerede HPD?
• brug Tracer til at sammenligne de fælles bageste fordelinger af alphaog sigma2. Er disse parametre korreleret eller ukorreleret?
• sammenlign det tidligere gennemsnit med det bageste gennemsnit. (Tip: Brug det valgfrie argument underPrior=TRUE i funktionen mymcmc.run()) er de forskellige (f. eks.)? Er det bageste gennemsnit uden for det forudgående 95% sandsynlighedsinterval?

sammenligning af ou-og BM-modeller

nu hvor vi kan passe både BM-og OU-modeller, vil vi naturligvis gerne vide, hvilken model der passer bedre. I dette afsnit lærer vi, hvordan man bruger vendbar-jump Markov-kæde Monte Carlo til at sammenligne pasformen til ou-og BM-modeller.

modelvalg ved hjælp af Reversible-Jump MCMC

for at teste hypotesen om, at et tegn udvikler sig mod et selektivt optimum, forestiller vi os to modeller. Den første model, hvor der ikke er nogen tilpasning til det optimale, er tilfældet, når $\alpha = 0$. Den anden model svarer til ou-modellen med $\alpha > 0$. Dette fungerer, fordi brunisk bevægelse er et specielt tilfælde af ou-modellen, når tilpasningshastigheden er 0. Desværre, fordi $ \ alpha$ er en kontinuerlig parametre, vil en standard Markov-kæde aldrig besøge stater, hvor hver værdi er nøjagtigt lig med 0. Heldigvis kan vi bruge reversible jump for at give Markov-kæden mulighed for at overveje at besøge den brune bevægelsesmodel. Dette indebærer at specificere den forudgående sandsynlighed på hver af de to modeller og give den forudgående distribution for $\alpha$ for OU-modellen.

brug af rjMCMC gør det muligt for Markov-kæden at besøge de to modeller i forhold til deres bageste Sandsynlighed. Den bageste Sandsynlighed for model $i$ er simpelthen den brøkdel af prøver, hvor kæden besøgte den model. Fordi vi også angiver en prior på modellerne, kan vi beregne en Bayes-faktor for ou-modellen som:

\

hvor $P( \tekst{OU model} \mid H)$ og $P( \tekst{OU model})$ er henholdsvis den bageste sandsynlighed og den tidligere Sandsynlighed for OU-modellen.

Vendbar-spring mellem ou-og BM-modeller

for at aktivere rjMCMC er vi simpelthen nødt til at placere et vendbart Spring forud for den relevante parameter, $\alpha$. Vi kan ændre prior på alpha, så det tager enten en konstant værdi på 0 eller trækkes fra en forudgående distribution. Endelig angiver vi en forudgående sandsynlighed på OU-modellen på p = 0.5.

alpha ~ dnReversibleJumpMixture(0.0, dnExponential(10), 0.5)

vi leverer derefter et vendbart springforslag på alpha, der foreslår ændringer mellem de to modeller.

moves.append( mvRJSwitch(alpha, weight=1.0) )

derudover leverer vi det normale mvScale forslag til, hvornår MCMC besøger ou-modellen.

moves.append( mvScale(alpha, weight=1.0) )

vi inkluderer en variabel, der har en værdi på 1, når kæden besøger OU-modellen, og en tilsvarende variabel, der har værdi 1, når den besøger BM-modellen. Dette giver os mulighed for let at beregne den bageste Sandsynlighed for modellerne, fordi vi simpelthen har brug for at beregne den bageste middelværdi af denne parameter.

is_OU := ifelse(alpha != 0.0, 1, 0)is_BM := ifelse(alpha == 0.0, 1, 0)

fraktionen af prøver, for hvilke is_OU = 1 er den bageste Sandsynlighed for ou-modellen. Alternativt svarer det bageste gennemsnitlige skøn over denne indikatorvariabel til den bageste Sandsynlighed for OU-modellen. Disse værdier kan bruges i Bayes-Faktorligningen ovenfor til at beregne Bayes-Faktorstøtten til begge modeller.

1. Felsenstein J. 1985. Fylogenier og den komparative metode. Den Amerikanske Naturforsker.:1-15.10.1086/284325
2. H. H., Heath T. A., Boussau B., Landis M. J., Ronk F., Huelsenbeck J. P. 2014. Probabilistisk grafisk model repræsentation i fylogenetik. Systematisk Biologi. 63: 753-771.10.1093/sysbio/syu039
3. Landis M. J., Schraiber J. G. 2017. Pulserende evolution formet moderne hvirveldyr kropsstørrelser. Forløbet af National Academy of Sciences. 114: 13224-13229.10. 1073 / pnas.1710920114