Enkle Ornstein-Uhlenbeck Modeller

Estimering Av Evolusjonær Optima

denne opplæringen viser hvordan man spesifiserer En Ornstein-Uhlenbeck-modell hvor den optimale fenotypen antas å være konstant blant grener av en tidskalibrert fylogeni (manglende referanse) ved hjelp av datasettene av (log) kroppsstørrelse over vertebrate clades fra (manglende referanse). Vi gir probabilistisk grafisk modell representasjon av hver komponent for denne opplæringen. Etter å ha spesifisert modellen, vil Du estimere parametrene Til Ornstein-Uhlenbeck evolution ved Hjelp Av Markov chain Monte Carlo (MCMC).

Ornstein-Uhlenbeck-Modellen

under Den enkle Ornstein-Uhlenbeck (OU) – modellen antas en kontinuerlig karakter å utvikle seg mot en optimal verdi, $\theta$. Tegnet utvikler seg stokastisk i henhold til en driftparameter, $\sigma^2$. Tegnet trekkes mot det optimale ved tilpasningsgraden, $ \ alpha$; større verdier av alfa indikerer at tegnet trekkes sterkere mot $\theta$. Når tegnet beveger seg bort fra $\theta$, bestemmer parameteren $ \ alpha$ hvor sterkt tegnet trekkes tilbake. Av denne grunn blir $\alpha$ noen ganger referert til som en» gummibånd » – parameter. Når tilpasningsparameteren $ \ alpha = 0$, kollapser ou-modellen TIL BM-modellen. Den resulterende grafiske modellen er ganske enkel, da sannsynligheten for de kontinuerlige tegnene bare avhenger av fylogenien (som vi antar å være kjent i denne opplæringen) og tre ou-parameteren ().

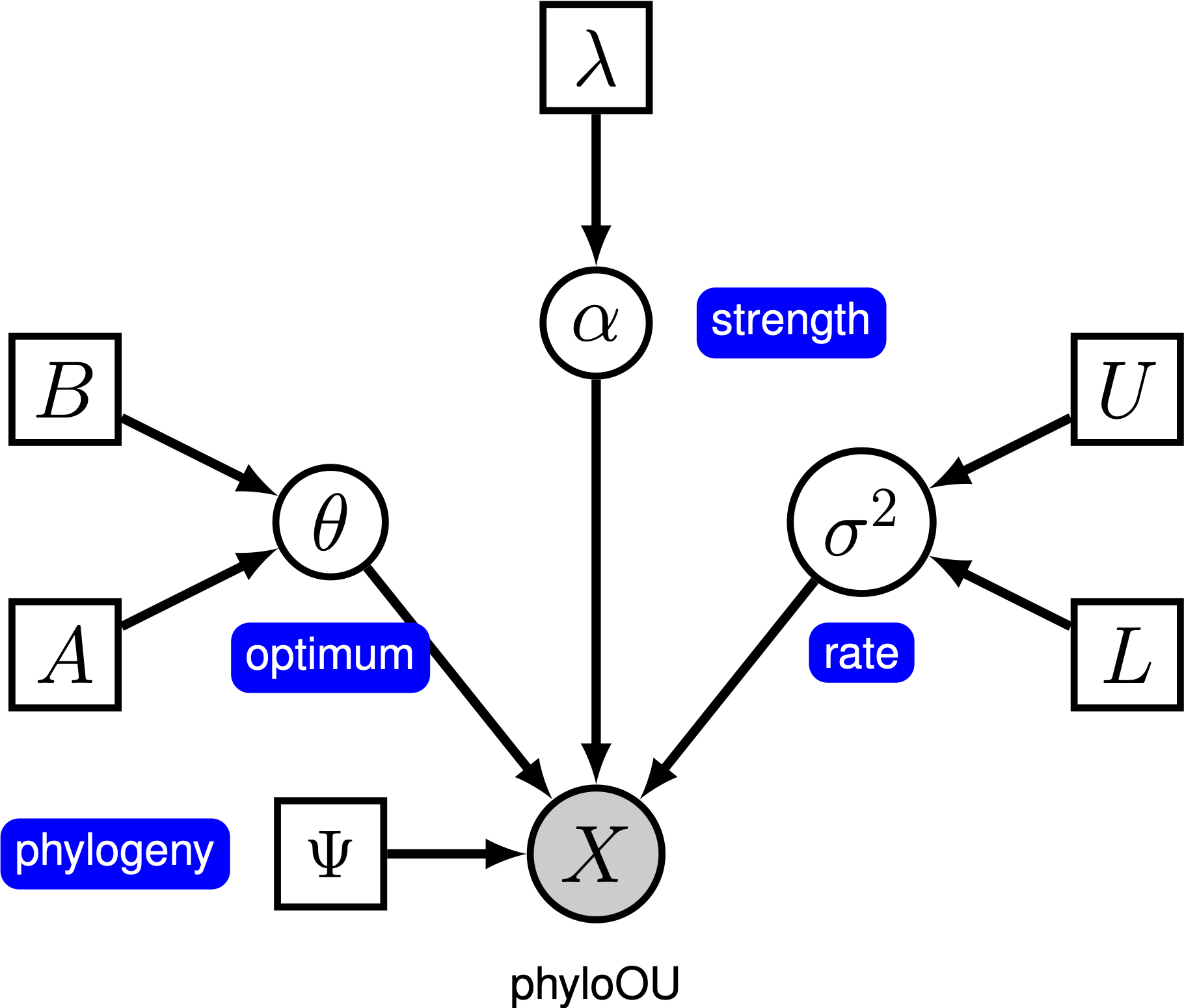
i denne opplæringen bruker vi 66 vertebrate phylogenies og (log) kroppsstørrelse datasett Fra (Landis And Schraiber 2017).

⇨ den fulle ou-modellspesifikasjonen finnes i filen som heter mcmc_OU.Rev.

Les dataene

vi begynner med å bestemme hvilket av de 66 vertebrate datasettene Som skal brukes. Her antar vi at vi analyserer Det første datasettet (Acanthuridae), men du bør gjerne velge noen av datasettene.

dataset <- 1

Nå leser vi i det (tidskalibrerte) treet som svarer til vårt valgte datasett.

T <- readTrees("data/trees.nex")

Deretter leser vi i tegndataene for samme datasett.

data <- readContinuousCharacterData("data/traits.nex")

I Tillegg initialiserer vi en variabel for vår vektor ofmoves og skjermer:

moves = VectorMoves()monitors = VectorMonitors()

Angi modellen

tremodell

i denne opplæringen antar vi at treet er kjent uten område. Vi lager en konstant knute for treet som tilsvarer den observerte fylogenien.

tree <- T

Rate parameter

den stokastiske utviklingshastigheten styres av rate parameter, $\sigma^2$. Vi tegner hastighetsparameteren fra en loguniform tidligere. Denne prioren er ensartet på loggskalaen, noe som betyr at den representerer uvitenhet om størrelsesordenen av frekvensen.

sigma2 ~ dnLoguniform(1e-3, 1)

For å estimere den bakre fordelingen av $ \ sigma^2$, må vi gi EN MCMC forslagsmekanisme som opererer på denne noden. Fordi $\sigma^2$ er en rate parameter, og må derfor være positiv, bruker vi et skaleringsflyt kalt mvScale.

moves.append( mvScale(sigma2, weight=1.0) )

Tilpasningsparameter

tilpasningshastigheten mot det optimale bestemmes av parameteren $ \ alpha$. Vi tegner $ \ alpha$ fra en eksponentiell tidligere distribusjon, og legger et skalaforslag på det.

alpha ~ dnExponential(10)moves.append( mvScale(alpha, weight=1.0) )

Optimum

vi tegner den optimale verdien fra en vag uniform prior fra -10 til 10 (du bør endre dette før hvis karakteren din er utenfor dette området). Fordi denne parameteren kan være positiv eller negativ, bruker vi et lysbilde flytte å foreslå endringer UNDER MCMC.

theta ~ dnUniform(-10, 10)moves.append( mvSlide(theta, weight=1.0) )

Ornstein-Uhlenbeck modell

Nå som vi har spesifisert parametrene til modellen, kan vi tegne tegndataene fra den tilsvarende fylogenetiske ou-modellen. I dette eksemplet bruker VI reml-algoritmen til å beregne sannsynligheten effektivt (Felsenstein 1985). Vi antar at tegnet begynner på den optimale verdien ved roten av treet.

X ~ dnPhyloOrnsteinUhlenbeckREML(tree, alpha, theta, sigma2^0.5, rootStates=theta)

Å Merke seg at $X$ er de observerte dataene (), klemmer vi data til denne stokastiske noden.

X.clamp(data)

Til slutt lager vi et arbeidsområdeobjekt for hele modellen med model(). Husk at arbeidsområdeobjekter initialiseres med operatøren =, og er ikke selv en Del Av den Bayesianske grafiske modellen. Funksjonen model() krysser hele modellgrafen og finner alle noder i modellen som vi angav. Dette objektet gir en praktisk måte å referere til hele modellobjektet, i stedet for bare EN ENKELT dag-node.

mymodel = model(theta)

Kjører EN MCMC-analyse

Spesifiserer Skjermer

FOR VÅR MCMC-analyse må vi sette opp en vektor av skjermer for å registrere tilstandene Til Vår Markov-kjede. Skjermfunksjonene kalles alle mn*, der * er jokertegnet som representerer skjermtypen. Først vil vi initialisere modellmonitoren ved hjelp av funksjonen mnModel. Dette skaper en ny skjermvariabel som vil sende ut tilstandene for alle modellparametere når de sendes inn I EN MCMC-funksjon.

monitors.append( mnModel(filename="output/simple_OU.log", printgen=10) )

i tillegg oppretter du en skjermskjerm som vil rapportere tilstandene til spesifiserte variabler til skjermen med mnScreen:

monitors.append( mnScreen(printgen=1000, sigma2, alpha, theta) )

Ved Å Initialisere OG Kjøre MCMC-Simuleringen

med en fullt spesifisert modell, et sett med skjermer og et sett med trekk, kan wecan nå sette OPP MCMC-algoritmen som vil prøve parameterverdier inproportion til deres bakre sannsynlighet. Funksjonen mcmc() vilopprett VÅRT MCMC-objekt:

mymcmc = mcmc(mymodel, monitors, moves, nruns=2, combine="mixed")

kjør NÅ MCMC:

mymcmc.run(generations=50000)

Når analysen er fullført, vil du ha de overvåkede filene i youroutput-katalogen.

⇨ Rev filen for å utføre denne analysen: mcmc_OU.Rev

Tegn som utvikler seg under ou-prosessen, vil ha en stasjonær fordeling, som er en normal fordeling med gjennomsnittlig $\theta$ og varians $ \ sigma^2 \ div 2 \ alpha$. Derfor, hvis utviklingshastighetene er høye (eller grenene i treet er relativt lange), kan det være vanskelig å estimere $\sigma^2$ og $\alpha$ separat, siden de begge bestemmer den langsiktige variansen av prosessen. Vi kan se om dette påvirker vår analyse ved å undersøke felles bakre fordeling av parametrene i Tracer. Når parametrene er positivt korrelerte, bør vi nøle med å tolke deres marginale fordelinger (dvs. ikke gjør avledninger om tilpasningsgraden eller variansparameteren separat).

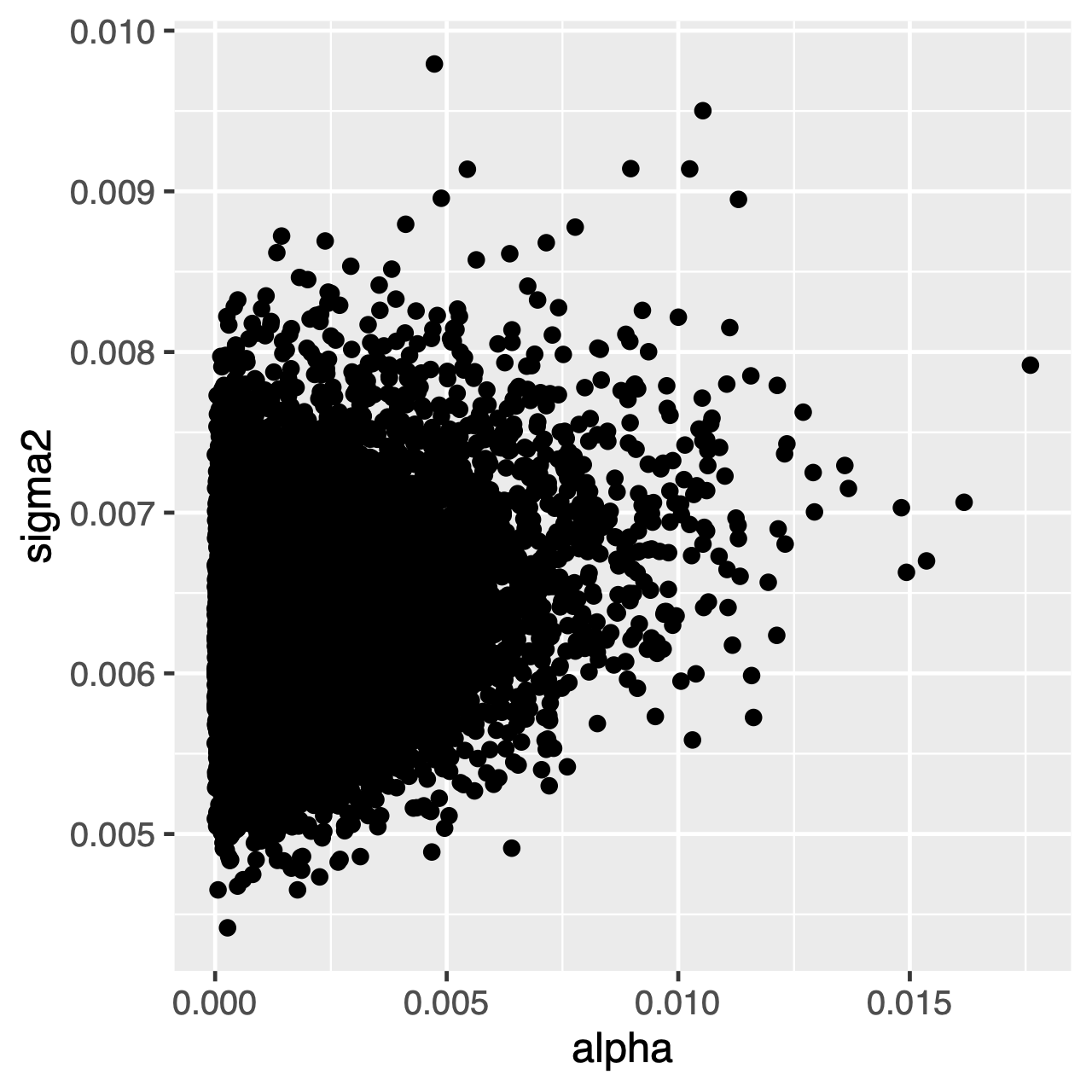
Øvelse 1

• Kjør EN MCMC-simulering for å estimere den bakre fordelingen AV ou optimum (theta).
• Last den genererte utdatafilen inn i Tracer : hva er gjennomsnittlig bakre estimat av theta og hva er estimert HPD?
• Bruk Tracer for å sammenligne felles bakre fordelinger av alpha og sigma2. Er disse parametrene korrelerte eller ukorrelerte?
• Sammenlign det tidligere gjennomsnittet med det bakre gjennomsnittet. (Hint: Bruk det valgfrie argumentet underPrior=TRUE i funksjonen mymcmc.run()) er de forskjellige (f. eks.)? Er det bakre gjennomsnittet utenfor det tidligere 95% sannsynlighetsintervallet?

Sammenligning AV ou-og BM-modeller

Nå som vi kan passe BÅDE BM-og OU-modeller, kan vi naturligvis vite hvilken modell som passer bedre. I denne delen lærer vi hvordan du bruker reversibel-jump Markov-kjeden Monte Carlo for å sammenligne passformen TIL OU og BM-modeller.

Modellvalg Ved Hjelp Av Reversibel HOPP MCMC

for å teste hypotesen om at et tegn utvikler seg mot et selektivt optimum, forestiller vi oss to modeller. Den første modellen, der det ikke er noen tilpasning mot det optimale, er tilfellet når $ \ alpha = 0$. Den andre modellen tilsvarer ou-modellen med $ \ alpha > 0$. Dette fungerer fordi Brownsk bevegelse er et spesielt tilfelle AV ou-modellen når tilpasningsgraden er 0. Dessverre, fordi $ \ alpha$ er en kontinuerlig parameter, vil En Standard Markov-kjede aldri besøke stater der hver verdi er nøyaktig lik 0. Heldigvis kan Vi bruke reversible jump for Å tillate Markov-kjeden å vurdere å besøke Brownian-motion-modellen. Dette innebærer å spesifisere den tidligere sannsynligheten på hver av de to modellene, og gi den tidligere fordelingen for $\alpha$ for OU-modellen.

Ved hjelp Av Rjmcmc Kan Markov-kjeden besøke de to modellene i forhold til deres bakre sannsynlighet. Den bakre sannsynligheten for modell $i$ er ganske enkelt brøkdelen av prøver hvor kjeden besøkte den modellen. Fordi vi også spesifiserer en prior på modellene, kan vi beregne En Bayes-Faktor for OU-modellen som:

\

hvor $P (\text{ou model} \mid X)$ og $P (\text{ou model})$ er henholdsvis bakre sannsynlighet og tidligere sannsynlighet for OU-modellen.

Reversibel-hopp mellom OU og BM modeller

for å aktivere rjMCMC, må vi bare plassere et reversibelt hopp før den aktuelle parameteren, $\alpha$. Vi kan endre prioren på alpha slik at den tar enten en konstant verdi på 0, eller trekkes fra en tidligere distribusjon. Til slutt angir vi en tidligere sannsynlighet på ou-modellen av p = 0.5.

alpha ~ dnReversibleJumpMixture(0.0, dnExponential(10), 0.5)

Vi gir deretter et reversibelt hoppforslag på alpha som foreslår endringer mellom de to modellene.

moves.append( mvRJSwitch(alpha, weight=1.0) )

I Tillegg gir vi det normale mvScale – forslaget for NÅR MCMC besøker ou-modellen.

moves.append( mvScale(alpha, weight=1.0) )

vi inkluderer en variabel som har en verdi på 1 når kjeden besøker OU-modellen, og en tilsvarende variabel som har verdi 1 når DEN besøker BM-modellen. Dette vil tillate oss å enkelt beregne den bakre sannsynligheten for modellene fordi vi bare trenger å beregne den bakre middelverdien av denne parameteren.

is_OU := ifelse(alpha != 0.0, 1, 0)is_BM := ifelse(alpha == 0.0, 1, 0)

fraksjonen av prøver som is_OU = 1 er den bakre sannsynligheten FOR OU-modellen. Alternativt tilsvarer det bakre gjennomsnittlige estimatet av denne indikatorvariabelen den bakre sannsynligheten FOR OU-modellen. Disse verdiene kan brukes i bayes-Faktorligningen ovenfor for å beregne Bayes-Faktorstøtten for begge modellene.

1. Felsenstein J. 1985. Fylogenier og komparativ metode. Den Amerikanske Naturforskeren.:1-15.10.1086/284325
2. Hö S., Heath T. A., Boussau B., Landis M. J., Ronquist F., Huelsenbeck J. P. 2014. Probabilistisk Grafisk Modell Representasjon I Fylogenetikk. Systematisk Biologi. 63: 753-771. 10. 1093/sysbio / syu039
3. Landis M. J., Schraiber J. G. 2017. Pulserende evolusjon formet moderne virveldyr kroppsstørrelser. Proceedings Av Det Nasjonale Vitenskapsakademiet. 114: 13224-13229.10. 1073/pnas.1710920114