enkla Ornstein-Uhlenbeck modeller

Estimating Evolutionary Optima

denna handledning visar hur man specificerar en Ornstein-Uhlenbeck-modell där den optimala fenotypen antas vara konstant bland grenar av en tidskalibrerad fylogeni (saknad referens) med hjälp av dataset av (log) kroppsstorlek över ryggradsdjur från (saknad referens). Vi tillhandahåller den probabilistiska grafiska modellrepresentationen för varje komponent för denna handledning. När du har angett modellen kommer du att uppskatta parametrarna för Ornstein-Uhlenbeck evolution med Markov chain Monte Carlo (MCMC).

Ornstein-Uhlenbeck-modellen

Under den enkla Ornstein-Uhlenbeck (OU) – modellen antas en kontinuerlig karaktär utvecklas mot ett optimalt värde, $\theta$. Karaktären utvecklas stokastiskt enligt en driftparameter, $ \ sigma^2$. Karaktären dras mot det optimala av anpassningsgraden, $ \ alpha$; större värden av alfa indikerar att tecknet dras starkare mot $\theta$. När tecknet rör sig bort från $\theta$ bestämmer parametern $\alpha$ hur starkt tecknet dras tillbaka. Av denna anledning kallas $\alpha$ ibland som en” gummiband ” – parameter. När hastigheten för anpassningsparametern $ \ alpha = 0$ kollapsar OU-modellen till BM-modellen. Den resulterande grafiska modellen är ganska enkel, eftersom sannolikheten för de kontinuerliga tecknen bara beror på fylogeni (som vi antar är känd i denna handledning) och tre ou-parametern ().

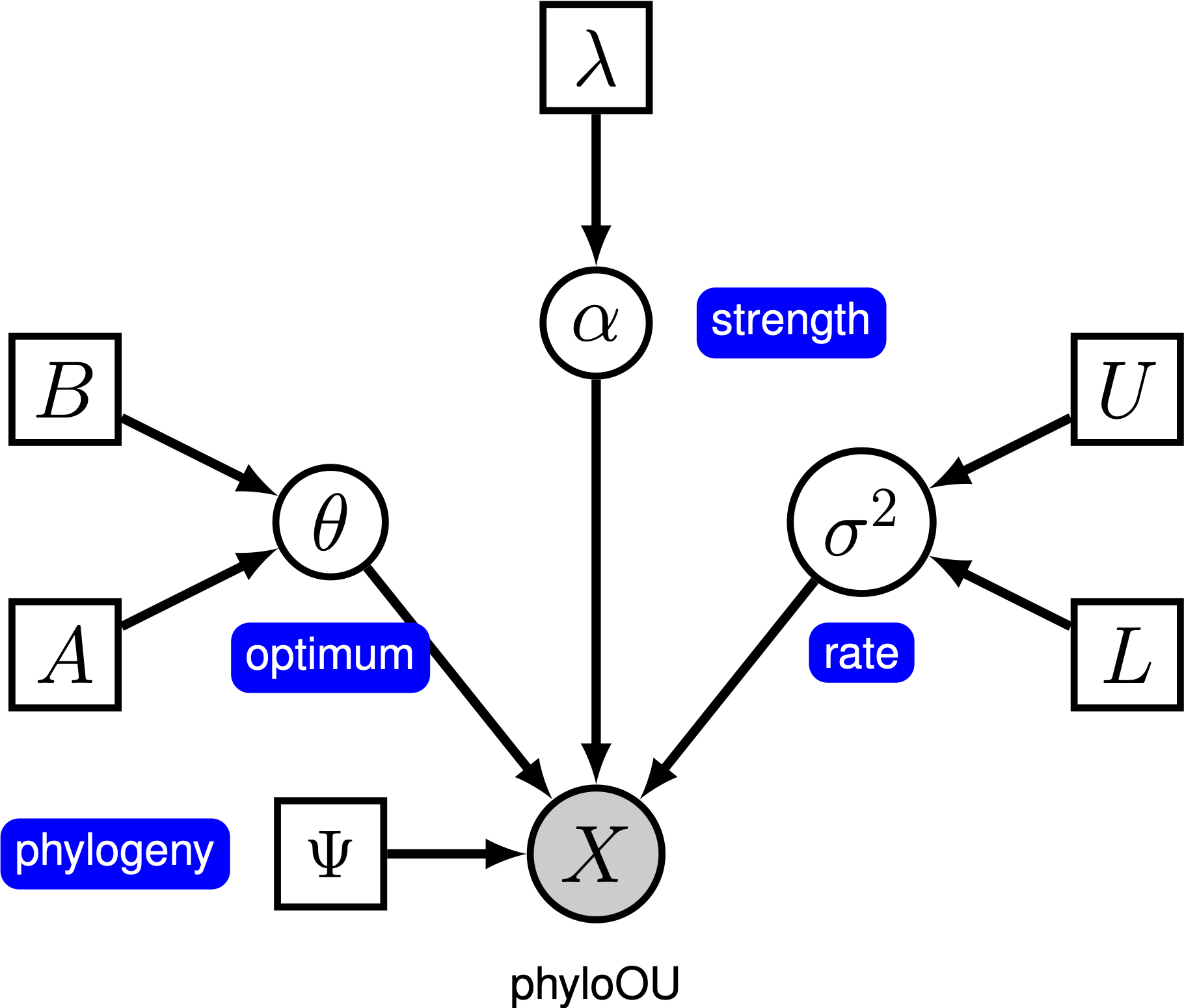
i denna handledning använder vi 66 ryggradsfylogenier och (log) kroppsstorleksdataset från (Landis och Schraiber 2017).

bisexuell den fullständiga ou-modellspecifikationen finns i filen mcmc_OU.Rev.

Läs data

vi börjar med att bestämma vilken av de 66 ryggradsdatauppsättningarna som ska användas. Här antar vi att vi analyserar den första datauppsättningen (Acanthuridae), men du borde gärna välja någon av datauppsättningarna.

dataset <- 1

nu läser vi i det (tidskalibrerade) trädet som motsvarar vår valda dataset.

T <- readTrees("data/trees.nex")

därefter läser vi i teckendata för samma dataset.

data <- readContinuousCharacterData("data/traits.nex")

dessutom initierar vi en variabel för vår Vektor ofmoves och monitorer:

moves = VectorMoves()monitors = VectorMonitors()

ange modellen

Trädmodell

i denna handledning antar vi att trädet är känt utan område. Vi skapar en konstant nod för trädet som motsvarar den observerade fylogeni.

tree <- T

Hastighetsparameter

den stokastiska utvecklingshastigheten styrs av hastighetsparametern, $\sigma^2$. Vi ritar hastighetsparametern från en loguniform prior. Denna prior är enhetlig på log skala, vilket innebär att det är representerar okunnighet om storleksordningen av hastigheten.

sigma2 ~ dnLoguniform(1e-3, 1)

för att uppskatta den bakre fördelningen av $\sigma^2$ måste vi tillhandahålla en MCMC-förslagsmekanism som fungerar på denna nod. Eftersom $ \ sigma^2$ är en hastighetsparameter och därför måste vara positiv använder vi en skalningsrörelse som heter mvScale.

moves.append( mvScale(sigma2, weight=1.0) )

anpassningsparameter

anpassningshastigheten mot det optimala bestäms av parametern $\alpha$. Vi drar $ \ alpha$ från en exponentiell tidigare distribution och lägger ett skalförslag på det.

alpha ~ dnExponential(10)moves.append( mvScale(alpha, weight=1.0) )

Optimum

vi drar det optimala värdet från en vag enhetlig prior som sträcker sig från -10 till 10 (Du bör ändra detta tidigare om din karaktär ligger utanför detta intervall). Eftersom denna parameter kan vara positiv eller negativ använder vi en bildflyttning för att föreslå ändringar under MCMC.

theta ~ dnUniform(-10, 10)moves.append( mvSlide(theta, weight=1.0) )

Ornstein-Uhlenbeck-modellen

nu när vi har angett parametrarna för modellen kan vi rita teckendata från motsvarande fylogenetiska OU-modell. I det här exemplet använder vi REML-algoritmen för att effektivt beräkna sannolikheten (Felsenstein 1985). Vi antar att karaktären börjar med det optimala värdet vid trädets rot.

X ~ dnPhyloOrnsteinUhlenbeckREML(tree, alpha, theta, sigma2^0.5, rootStates=theta)

notera att $X$ är de observerade data (), vi klämmer fast data till denna stokastiska nod.

X.clamp(data)

slutligen skapar vi ett arbetsytaobjekt för hela modellen med model(). Kom ihåg att arbetsyteobjekt initieras med operatören = och inte själva ingår i den bayesiska grafiska modellen. Funktionen model() går igenom hela modelldiagrammet och hittar alla noder i modellen som vi angav. Detta objekt ger ett bekvämt sätt att hänvisa till hela modellobjektet, snarare än bara en enda dag-nod.

mymodel = model(theta)

kör en MCMC-analys

specificera bildskärmar

för vår MCMC-analys måste vi skapa en vektor av bildskärmar för att registrera tillstånden i vår Markov-kedja. Monitorfunktionerna kallas alla mn*, där * är jokertecknet som representerar bildskärmstypen. Först kommer vi att initiera modellmonitorn med funktionen mnModel. Detta skapar en ny monitorvariabel som matar ut tillstånden för alla modellparametrar när de överförs till en MCMC-funktion.

monitors.append( mnModel(filename="output/simple_OU.log", printgen=10) )

skapa dessutom en skärmskärm som rapporterar tillstånden för specificerade variabler till skärmen med mnScreen:

monitors.append( mnScreen(printgen=1000, sigma2, alpha, theta) )

initialisering och körning av MCMC-simuleringen

med en helt specificerad modell, en uppsättning bildskärmar och en uppsättning rörelser, kan wecan nu ställa in MCMC-algoritmen som kommer att sampla parametervärden inproportion till deras bakre Sannolikhet. Funktionen mcmc() kommer att skapa vårt MCMC-objekt:

mymcmc = mcmc(mymodel, monitors, moves, nruns=2, combine="mixed")

kör nu MCMC:

mymcmc.run(generations=50000)

när analysen är klar kommer du att ha de övervakade filerna i dinutput-katalog.

Brasilien filen Rev för att utföra denna analys: mcmc_OU.Rev

tecken som utvecklas under OU-processen tenderar mot en stationär distribution, vilket är en normalfördelning med medelvärde $\theta$ och varians $\sigma^2 \div 2\alpha$. Om utvecklingsgraden är hög (eller grenarna i trädet är relativt långa) kan det därför vara svårt att uppskatta $\sigma^2$ och $\alpha$ separat, eftersom de båda bestämmer processens långsiktiga varians. Vi kan se om detta påverkar vår analys genom att undersöka den gemensamma bakre fördelningen av parametrarna i Tracer. När parametrarna är positivt korrelerade bör vi tveka att tolka deras marginella fördelningar (dvs. inte dra slutsatser om anpassningsgraden eller variansparametern separat).

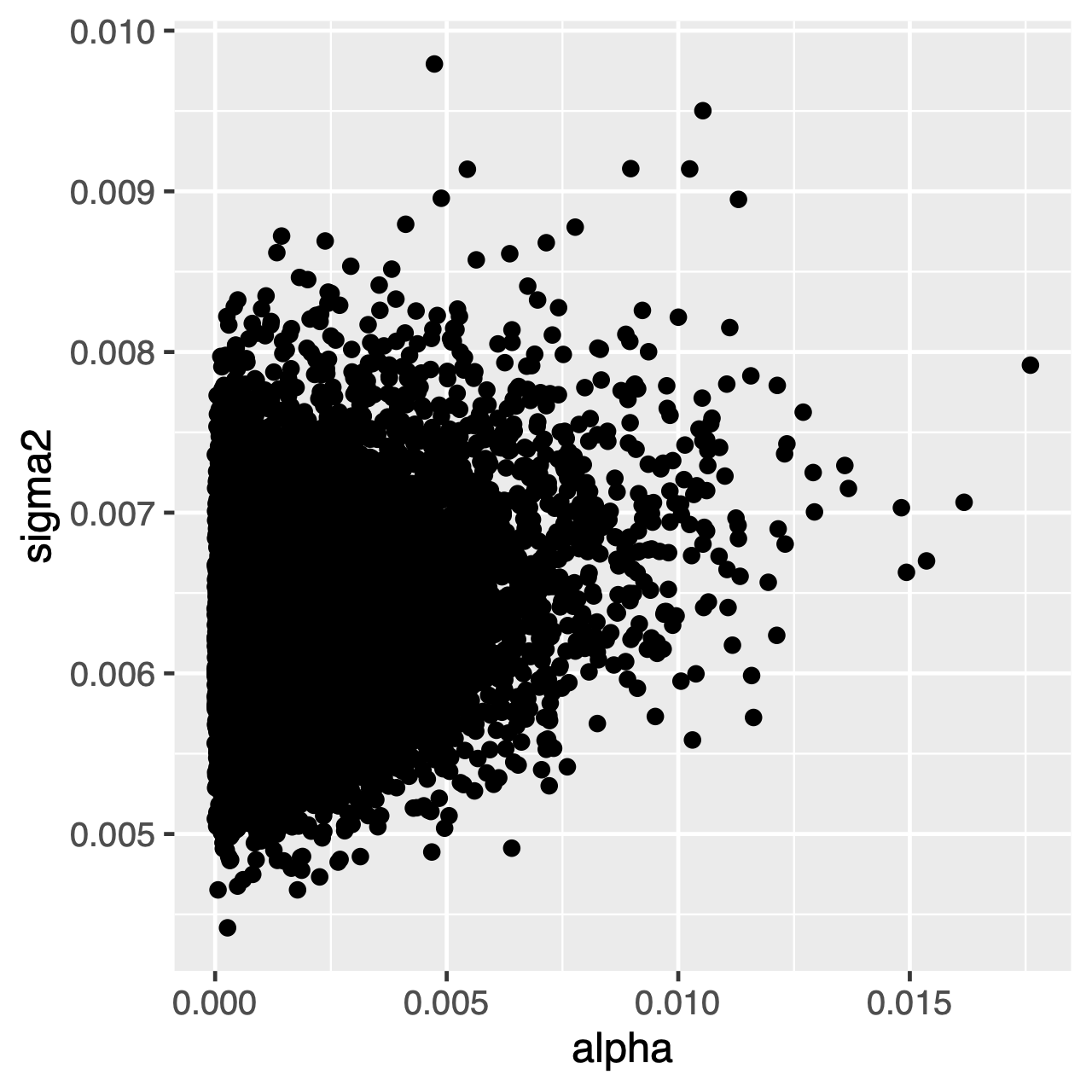
Övning 1

• kör en MCMC-simulering för att uppskatta den bakre fördelningen av ou optimum (theta).
• ladda den genererade utdatafilen till Tracer: Vad är den genomsnittliga bakre uppskattningen av theta och vad är den beräknade HPD?
• använd Tracer för att jämföra de gemensamma bakre fördelningarna av alphaoch sigma2. Är dessa parametrar korrelerade eller okorrelerade?
• jämför det tidigare medelvärdet med det bakre medelvärdet. (Tips: Använd det valfria argumentet underPrior=TRUE i funktionen mymcmc.run() ) är de olika (t. ex.)? Är det bakre medelvärdet utanför det tidigare 95% sannolikhetsintervallet?

jämför Ou-och BM-modeller

nu när vi kan passa både BM-och OU-modeller kanske vi naturligtvis vill veta vilken modell som passar bättre. I det här avsnittet lär vi oss att använda reversibel-jump Markov-kedjan Monte Carlo för att jämföra passformen för OU-och BM-modellerna.

modellval med reversibel-Jump MCMC

för att testa hypotesen att ett tecken utvecklas mot ett selektivt optimalt, föreställer vi oss två modeller. Den första modellen, där det inte finns någon anpassning mot det optimala, är fallet när $\alpha = 0$. Den andra modellen motsvarar OU-modellen med $\alpha > 0$. Detta fungerar eftersom Brownsk rörelse är ett speciellt fall av OU-modellen när anpassningsgraden är 0. Tyvärr, eftersom $\alpha$ är en kontinuerlig parametrar, kommer en standard Markov-kedja aldrig att besöka stater där varje värde är exakt lika med 0. Lyckligtvis kan vi använda reversibelt hopp för att tillåta Markov-kedjan att överväga att besöka Brownsk-motion-modellen. Detta innebär att specificera den tidigare sannolikheten på var och en av de två modellerna och tillhandahålla den tidigare fördelningen för $\alpha$ för OU-modellen.

med Rjmcmc kan Markov-kedjan besöka de två modellerna i proportion till deras bakre Sannolikhet. Den bakre sannolikheten för modell $i$ är helt enkelt den bråkdel av prover där kedjan besökte den modellen. Eftersom vi också anger en prior på modellerna kan vi beräkna en Bayes-faktor för OU-modellen som:

\

där $P( \text{ou model} \mid X)$ och $P( \text{ou model})$ är den bakre sannolikheten respektive den tidigare sannolikheten för OU-modellen.

reversibel-hoppa mellan Ou-och BM-modeller

för att aktivera rjMCMC måste vi helt enkelt placera ett reversibelt hopp före den relevanta parametern, $\alpha$. Vi kan ändra prior på alpha så att det tar antingen ett konstant värde på 0, eller dras från en tidigare distribution. Slutligen anger vi en tidigare sannolikhet på OU-modellen av p = 0.5.

alpha ~ dnReversibleJumpMixture(0.0, dnExponential(10), 0.5)

vi ger sedan ett reversibelt hoppförslag på alpha som föreslår förändringar mellan de två modellerna.

moves.append( mvRJSwitch(alpha, weight=1.0) )

dessutom tillhandahåller vi det normala mvScale – förslaget för när MCMC besöker OU-modellen.

moves.append( mvScale(alpha, weight=1.0) )

vi inkluderar en variabel som har ett värde på 1 när kedjan besöker OU-modellen och en motsvarande variabel som har värde 1 när den besöker BM-modellen. Detta gör att vi enkelt kan beräkna modellernas bakre sannolikhet eftersom vi helt enkelt behöver beräkna det bakre medelvärdet för denna parameter.

is_OU := ifelse(alpha != 0.0, 1, 0)is_BM := ifelse(alpha == 0.0, 1, 0)

fraktionen av prover för vilka is_OU = 1 är den bakre sannolikheten för OU-modellen. Alternativt motsvarar den bakre genomsnittliga uppskattningen av denna indikatorvariabel den bakre sannolikheten för OU-modellen. Dessa värden kan användas i Bayes-Faktorekvationen ovan för att beräkna Bayes-Faktorstödet för endera modellen.

1. Felsenstein J. 1985. Fylogenier och den jämförande metoden. Den Amerikanska Naturforskaren.:1-15.10.1086/284325
2. H. S. S., Heath T. A., Boussau B., Landis M. J., Ronquist F., Huelsenbeck J. P. 2014. Probabilistisk grafisk Modellrepresentation i fylogenetik. Systematisk Biologi. 63: 753-771.10. 1093/sysbio / syu039
3. Landis M. J., Schraiber J. G. 2017. Pulserad evolution formad moderna ryggradsdjur kroppsstorlekar. Proceedings av National Academy of Sciences. 114: 13224-13229.10.1073/pnas.1710920114