Riemannův Tenzor

Riemannův tenzor (Schutz 1985) , také známý Riemann-Christoffel tenzor křivosti (Weinberg v roce 1972, str. 133; Arfken 1985, str. 123) nebo Riemannův tenzor křivosti (Misner et al. 1973, s. 218), je čtyřindexový tenzor, který je užitečný v obecné relativitě. Další důležité Obecné relativistické tenzory tak, že tenzor Ricciho zakřivení a skalární zakřivení lze definovat z hlediska .

Riemannův tenzor je v nějakém smyslu pouze tenzor, který může být zhotoven z metrického tenzoru a jeho první a druhé derivace,

(1)

kde Christoffel symboly prvního druhu a je čárkou derivace (Schmutzer 1968, str. 108; Weinberg v roce 1972). V jedné dimenzi . Ve čtyřech rozměrech je 256 komponent. Využití symetrie vztahů,

(2)

počet nezávislých složek je snížena na 36. Pomocí stavu

(3)

počet souřadnic snižuje na 21. Konečně, použití

(4)

20 nezávislé komponenty jsou vlevo (Misner et al. 1973, s. 220-221; Arfken 1985, s. 123-124).

obecně platí, že počet nezávislých složek v rozměry je dána

(5)

„čtyři-dimenzionální pyramidální čísla,“prvních pár hodnot, které jsou 0, 1, 6, 20, 50, 105, 196, 336, 540, 825, … (Úř.věst. A002415). Počet skalárních veličinách, které mohou být konstruovány z a

(6)

(Weinberg v roce 1972). Prvních několik hodnot je pak 0, 1, 3, 14, 40, 90, 175, 308, 504,780, … (Úř.věst. A050297).

z hlediska Jacobi tenzor ,

(7)

Nechte

(8)

pokud množství uvnitř Christoffel symbol druhého druhu. Pak

(9)

rozdělené na své nejjednodušší rozkladu v rozměry,

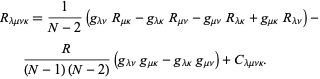(10)

Tady, je Ricciho tenzor křivosti, je skalární křivost, a je Weyl tenzor.