A de Riemann (Schutz 1985) 
, também conhecido Riemann-Christoffel curvatura de riemann (Weinberg, 1972, p. 133; Arfken 1985, p. 123) ou Riemann curvatura de riemann (misner é et al. 1973, p. 218), é um tensor de quatro índices que é útil na relatividade geral. Outros tensores relativísticos gerais importantes, tais como o tensor de curvatura de Ricci e a curvatura escalar, podem ser definidos em termos de 
.
A de Riemann, em algum sentido, o único tensor que pode ser construído doservidor tensor mī etrico e a sua primeira e segunda derivadas,
 |
(1)
|
onde 
são mbolos de primeiro tipo e 
é uma vírgula derivados (o Artista, 1968, p. 108; Weinberg, 1972). Numa dimensão, 
. Em quatro dimensões, existem 256 componentes. Fazendo uso da simetria de relações,
 |
(2)
|
o número de componentes independentes é reduzida para 36. Usando a condição de
 |
(3)
|
o número de coordenadas reduz a 21. Finalmente, usando
 |
(4)
|
20 componentes independentes que são de esquerda (misner é et al. 1973, pp. 220-221; Arfken 1985, pp. 123-124).
No geral, o número de componentes independentes em 
dimensões é dada por
 |
(5)
|
o “quatro-dimensional piramidal números,”os primeiros valores de que são 0, 1, 6, 20, 50, 105, 196, 336, 540, 825, … (OEIS A002415). O número de escalares que podem ser construídos a partir de 
e 
é
 |
(6)
|
(Weinberg, 1972). Os primeiros valores são então 0, 1, 3, 14, 40, 90, 175, 308, 504,780, … (OEIS A050297).
Em termos de Jacobi tensor 
,
 |
(7)
|
Deixe
 |
(8)
|
onde a quantidade dentro de 
é um símbolo de Christoffel de segundo tipo. Então …
 |
(9)
|
decomposto em sua forma mais simples decomposição em 
dimensões,
 |
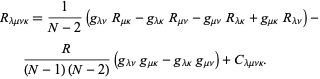(10)
|
Aqui, 
é o Ricci curvatura de riemann, 
é o escalar de curvatura, e 
é o tensor de Weyl.