de Riemann-tensor (Schutz 1985) 
, ook bekend als de Riemann-Christoffel-krommingssensor (Weinberg 1972, p. 133; Arfken 1985, p. 123) of Riemann-krommingssensor (Misner et al. 1973, p. 218), is een vier-index tensor die nuttig is in de algemene relativiteitstheorie. Andere belangrijke algemene relativistische tensoren, zodat de Ricci-krommingssensor en de scalaire kromming kunnen worden gedefinieerd in termen van 
.
De Riemann tensor is in zekere zin het enige tensor dat opgebouwd kan worden uit de metrische tensor en de eerste en tweede afgeleide,
 |
(1)
|
waar 
zijn de Christoffel symbolen van de eerste soort en 
is een komma afgeleide (Schmutzer 1968, blz. 108; Weinberg, 1972). In één dimensie, 
. In vier dimensies zijn er 256 componenten. Gebruik maken van de symmetrie relaties,
 |
(2)
|
het aantal onafhankelijke componenten wordt teruggebracht tot 36. Met behulp van de voorwaarde
 |
(3)
|
het aantal coördinaten daalt tot 21. Tot slot, met behulp van
 |
(4)
|
20 onafhankelijke componenten blijven over (Misner et al. 220-221; arfken 1985, blz. 123-124).
in het algemeen wordt het aantal onafhankelijke componenten met 
afmetingen gegeven door
 |
(5)
|
de “vierdimensionale piramidale getallen,” waarvan de eerste paar waarden zijn 0, 1, 6, 20, 50, 105, 196, 336, 540, 825, … (OEIS A002415). Het aantal scalaren dat kan worden geconstrueerd uit 
en 
is
 |
(6)
|
(Weinberg 1972). De eerste paar waarden zijn dan 0, 1, 3, 14, 40, 90, 175, 308, 504,780, … (OEIS A050297).
in termen van de Jacobi tensor 
,
 |
(7)
|
laat
 |
(8)
|
waarbij de hoeveelheid binnen de 
een Christoffelsymbool van de tweede soort is. Daarna
 |
(9)
|
uitgesplitst in zijn eenvoudigste afbraak in de 
afmetingen,
 |
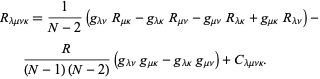(10)
|
hier is 
De Ricci-krommingssensor, 
de scalaire kromming en 
de Weyl-tensor.