Haushältertransformation
Haushältertransformation (auch „Haushälterreflexion“) ist eine orthogonale Reflexionstransformation:
- es berechnet die Vektoren in den Spalten der Matrix so, dass
- der erste Vektor alle Nullen außer dem ersten Element hat
Die Transformationsmatrix
Reflexionstransformation:
Eigenschaften
Haushaltsmatrizen sind symmetrisch und orthogonal: sie sind Reflexionsmatrizen
Ableitung
Wir haben also $P = I – 2vv^ T $:
Wir verwenden solche Transformationen zum Nullstellen von Elementen
QR-Zerlegung
Wie bei der LU-Zerlegung, bei der wir eine Reihe von Gauß-Transformationsänderungen angewendet haben, können wir dasselbe tun und eine Reihe von Haushältertransformationen durchführen
- Wenn wir also $ y = \pm e_1 $ auswählen (wobei $ e_1 $ die Matrix mit 1 an Position 1 und Rest sind Nullen)
- Dann werden alle Elemente von $ x $ außer dem ersten auf Null gesetzt
- durch die entsprechende Wahl von $ H $ können wir also $ A $ nehmen und alle Subdiagonalen auf Null setzen elemente
- können dies mehrmals für jede Spalte von $A$
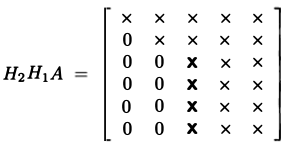
Auf diese Weise können wir QR-Zerlegung durchführen:
Hessenberg-Zerlegung
Anstatt die Matrix auf dreieckig zu reduzieren, können wir die Householder-Transformation verwenden, um eine Matrix auf die Hessenberg-Matrix zu reduzieren