jos olet lukenut edellisen postauksen siitä, mikä on induktori, edetkäämme seuraavalle tasolle, mikä on Induktanssi kaava piirejä.
nyt kun Kelan on lisätty luetteloon passiivisia elementtejä, on tarpeen laajentaa tehokas työkalu sarja-rinnakkainen yhdistelmä. Meidän täytyy tietää, miten löytää vastaava Induktanssi sarja-kytketty tai rinnakkain kytketty joukko induktorit löytyy käytännön piirejä.
sarjan induktorit
pitävät N-induktorien sarjaliitosta, kuten kuviosta käy ilmi.(1a), jossa vastaava piiri on esitetty kuvassa.(1b).
induktoreilla on sama virta niiden läpi. KVL: n soveltaminen silmukkaan,

korvaava vk= LK di / dt johtaa
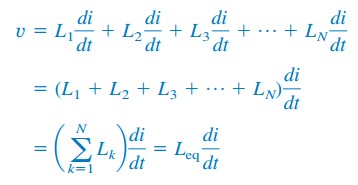
missä

näin,
sarjakytkettyjen induktoreiden ekvivalenttinen induktanssi on yksittäisten induktanssien summa.
sarjan induktorit yhdistetään täsmälleen samalla tavalla kuin sarjan vastukset.
yhdensuuntaiset induktorit
nyt tarkastellaan N-induktoreiden rinnakkaiskytkentää, kuten kuviosta käy ilmi.(2a), jossa vastaava piiri Kuvassa.(2b). Induktoreissa on sama jännite poikki. KCL: ää käyttäen

mutta

näin ollen,

missä
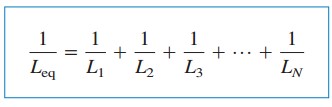
alkuperäinen nykyinen I (t0) kautta Leq at T= t0 odotetaan KCL on summa induktorivirrat T0. Näin ollen yhtälön mukaan.(5),
![]()
yhtälön mukaan.(6),
rinnakkaisinduktorien ekvivalenttinen induktanssi on yksittäisten induktanssien vastavuoroisuussumman käänteisarvo.
huomaa, että induktorit rinnakkain yhdistyvät samalla tavalla kuin vastukset rinnakkain.
kahdelle induktorille rinnakkain (N = 2), yhtälö.(6) tulee
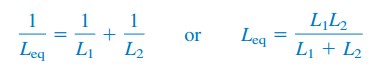
induktanssin Formula_3236>
1. Etsi vastaava Induktanssi piirin kuvassa.(3).
ratkaisu:
10-H -, 12-H-ja 20-H-induktorit ovat sarjassa; näin niiden yhdistäminen antaa 42-H-induktanssin. Tämä 42-H induktori on rinnakkain 7-H induktorin kanssa siten, että ne yhdistetään, jolloin saadaan

Tämä 6-H-induktori on sarjassa 4-H-ja 8-H-induktorien kanssa. Siksi,
![]()
2. Piirin Kuva.(4),
i(t) = 4(2 − e−10t) mA. Jos i2(0) = -1 mA, etsi:
(a) i1(0);
(b) v(t), v1(t) ja v2(t);
(c) i1(t) ja i2 (t).
ratkaisu:
(a) I (t) = 4 (2−e-10t) mA, i(0) = 4(2 − 1) = 4 äiti.
Since i = i1 + i2,
![]()
(b) The equivalent inductance is
![]()
Thus,


and


Since v = v1 + v2,
![]()
(C) nykyinen i1 saadaan

vastaavasti,

huomaa, että i1(t) + i2(t) = i (t).