Riemannin tensori (Schutz 1985) 
, tunnetaan myös Riemannin-Christoffelin kaarevuustensori (Weinberg 1972, s. 133; Arfken 1985, s.123) tai Riemannin kaarevuustensori (Misner et al. 1973, s.218) on yleisessä suhteellisuusteoriassa hyödyllinen neljän indeksin tensori. Muita tärkeitä yleisiä relativistisia tensoreita siten, että Riccin kaarevuustensori ja skalaarin kaarevuus voidaan määritellä arvoilla 
.
Riemannin tensori on jossain mielessä ainoa tensori, joka voidaan konstruoida metrisestä tensorista ja sen ensimmäisestä ja toisesta derivaatasta,
 |
(1)
|
missä 
ovat ensimmäisen laatuisia Christoffelin symboleja ja 
on pilkunjohdannainen (Schmutzer 1968, s. 108; Weinberg 1972). Yhdessä ulottuvuudessa 
. Neljässä ulottuvuudessa komponentteja on 256. Symmetriasuhteiden hyödyntäminen,
 |
(2)
|
riippumattomien komponenttien määrä vähenee 36: een. Ehdon käyttäminen
 |
(3)
|
koordinaattien määrä vähenee 21: een. Lopuksi käyttäen
 |
(4)
|
20 riippumattomat komponentit ovat jäljellä (Misner et al. 1973, s. 220-221;Arfken 1985, s. 123-124).
yleensä itsenäisten komponenttien lukumäärä 
mitoissa on annettu
 |
(5)
|
”neliulotteiset pyramidiluvut”, joiden ensimmäiset arvot ovat 0, 1, 6, 20, 50, 105, 196, 336, 540, 825, … (OEIS A002415). Skalaarien lukumäärä, joka voidaan konstruoida 
ja 
, on
 |
(6)
|
(Weinberg 1972). Ensimmäiset arvot ovat sitten 0, 1, 3, 14, 40, 90, 175, 308, 504,780, … (OEIS A050297).
Jakobien tensorin 
,
 |
(7)
|
Anna
 |
(8)
|
jossa 
sisällä oleva suure on toisen lajin Christoffel-symboli. Sitten
 |
(9)
|
jaoteltuna yksinkertaisimpaan hajoamiseensa 
mitoissa,
 |
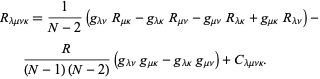(10)
|
tässä 
on Riccin kaarevuustensori, 
on skalaarin kaarevuustensori ja 
on Weyl-tensori.