Simple Ornstein-Uhlenbeck Models

Estimating Evolutionary Optima

this tutorial demonstrating how to specification an Ornstein-Uhlenbeck model where the optimal phenotype is experted to be constant among branches of a time-calibrated fylogeny (missing reference) using the datasets of (log) body-size across selkärankaisten clades from (missing reference). Tarjoamme probabilistinen graafinen malli esitys kunkin komponentin tämän opetusohjelma. Kun olet määrittänyt mallin, arvioit parametrit Ornstein-Uhlenbeck evoluution käyttäen Markovin ketju Monte Carlo (MCMC).

Ornstein-Uhlenbeck-malli

yksinkertaisen Ornstein-Uhlenbeck (OU) – mallin mukaan jatkuvan merkin oletetaan kehittyvän kohti optimaalista arvoa, $\theta$. Hahmo kehittyy stokastisesti drift-parametrin, $\sigma^2$mukaan. Hahmoa vetää kohti optimaalista sopeutumisnopeus, $\alpha$; suuremmat arvot alpha osoittavat, että merkki vedetään voimakkaammin kohti $\theta$. Hahmon siirtyessä poispäin $ \Theta$: sta parametri $\alpha$ määrittää, kuinka voimakkaasti hahmo vedetään takaisin. Tästä syystä, $\alpha$ kutsutaan joskus ”kuminauha” parametri. Kun sopeutumisnopeus parametri $\alpha = 0$, OU malli romahtaa BM malli. Tuloksena oleva graafinen malli on melko yksinkertainen, sillä jatkuvien merkkien todennäköisyys riippuu vain fylogeniasta (jonka oletamme olevan tiedossa tässä opetusohjelmassa) ja kolmesta ou-parametrista ().

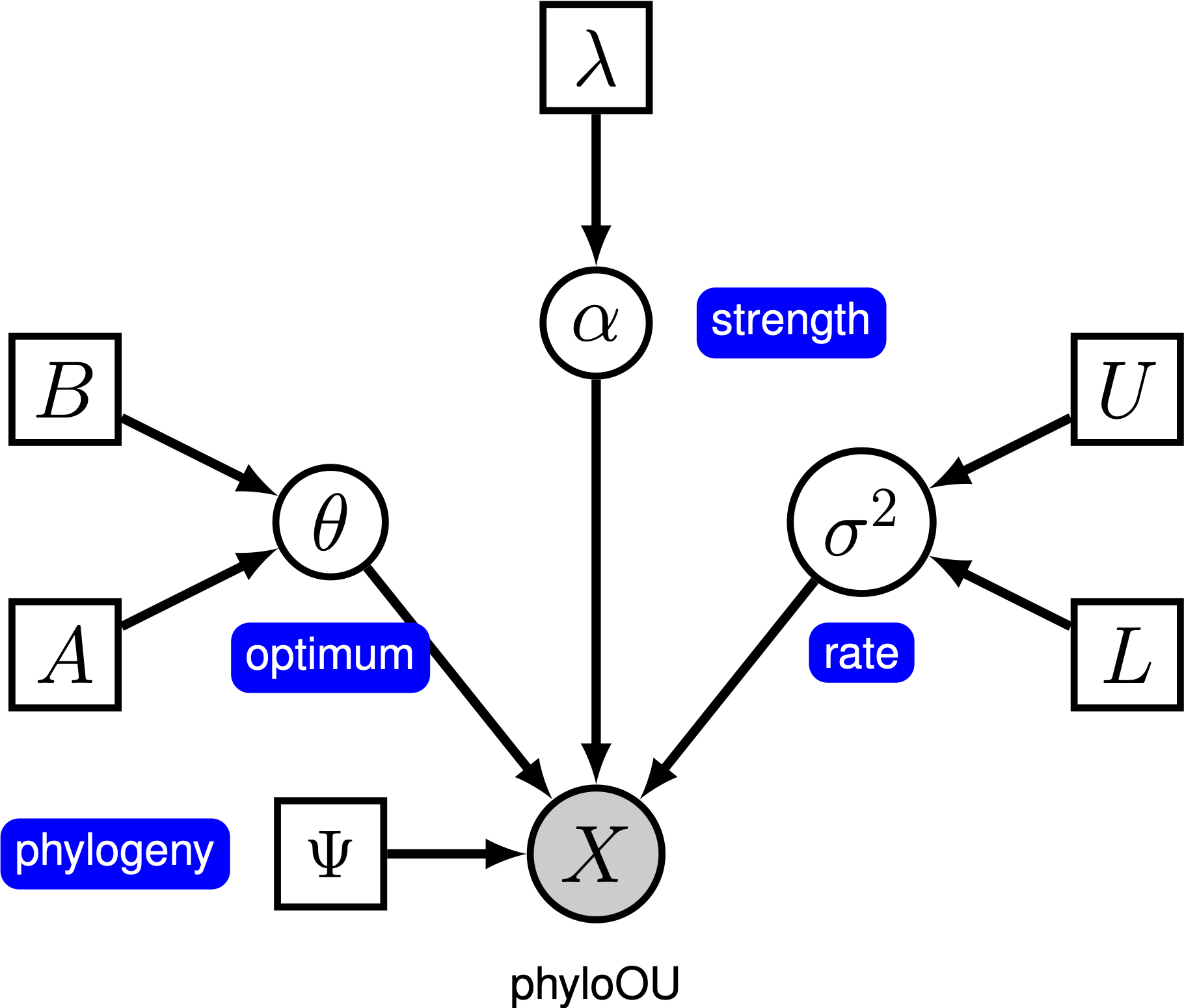
tässä opetusohjelmassa käytämme 66 selkärankaisten fylogeniaa ja (log) kehonkokoista aineistoa (Landis and Schraiber 2017).

⇨ koko OU-mallin spesifikaatio on tiedostossa nimeltään mcmc_OU.Rev.

Lue tiedot

aloitamme päättämällä, mitä 66 selkärankaisesta aineistosta käytetään. Täällä, oletamme analysoimme ensimmäisen aineiston (Acanthuridae), mutta sinun pitäisi vapaasti valita minkä tahansa aineiston.

dataset <- 1

nyt, luemme (aika-kalibroitu) puu vastaa valitsemaamme aineistoa.

T <- readTrees("data/trees.nex")

seuraavaksi luemme merkin tiedot saman aineiston.

data <- readContinuousCharacterData("data/traits.nex")

lisäksi alustamme muuttujan meidän vektori ofmoves ja näytöt:

moves = VectorMoves()monitors = VectorMonitors()

määrittelemällä mallin

Puumalli

tässä opetusohjelmassa oletetaan, että puu tunnetaan ilman pinta-alaa. Luomme puulle jatkuvan solmun, joka vastaa havaittua fylogeniaa.

tree <- T

Korkoparametria

stokastista evoluutionopeutta säätelee korkoparametri, $\sigma^2$. Piirrämme nopeus parametri loguniform prior. Tämä priori on log-asteikolla yhtenäinen, mikä tarkoittaa, että se edustaa tietämättömyyttä nopeuden suuruusjärjestyksestä.

sigma2 ~ dnLoguniform(1e-3, 1)

jotta voidaan arvioida posteriorijakauma $\sigma^2$, meidän täytyy tarjota MCMC ehdotus mekanismi, joka toimii tässä solmussa. Koska $\sigma^2$ on korkoparametri ja sen on siksi oltava positiivinen, käytämme skaalausliikettä nimeltä mvScale.

moves.append( mvScale(sigma2, weight=1.0) )

Sopeutumisparametri

sopeutumisnopeuden kohti optimia määrittää parametri $\alpha$. Arvomme $\alpha$ eksponentiaalisesta edeltävästä jakaumasta ja asetamme sille mittakaavaehdotuksen.

alpha ~ dnExponential(10)moves.append( mvScale(alpha, weight=1.0) )

optimi

saamme optimaalisen arvon epämääräisestä yhtenäisestä priori-arvosta, joka vaihtelee -10: stä 10: een (sinun tulisi muuttaa tätä priori-arvoa, jos hahmosi on tämän alueen ulkopuolella). Koska tämä parametri voi olla positiivinen tai negatiivinen, käytämme diasiirtoa ehdottaaksemme muutoksia MCMC: n aikana.

theta ~ dnUniform(-10, 10)moves.append( mvSlide(theta, weight=1.0) )

Ornstein-Uhlenbeck-malli

nyt kun mallin parametrit on määritelty, voidaan hahmotiedot piirtää vastaavasta fylogeneettisestä OU-mallista. Tässä esimerkissä, käytämme REML algoritmi tehokkaasti laskea todennäköisyys (Felsenstein 1985). Oletamme merkin alkavan optimaalisesta arvosta puun juuresta.

X ~ dnPhyloOrnsteinUhlenbeckREML(tree, alpha, theta, sigma2^0.5, rootStates=theta)

Huomatessamme, että $X$ on havaittu data (), kiinnitämme data tähän stokastiseen solmuun.

X.clamp(data)

lopuksi luodaan koko mallille työtilaobjekti, jossa on model(). Muista, että työtilan oliot on alustettu = – operaattorilla, eivätkä ne itse kuulu Bayesilaiseen graafiseen malliin. model() funktio kulkee koko mallikäyrän läpi ja löytää kaikki määrittämämme mallin solmut. Tämä objekti tarjoaa kätevän tavan viitata koko malliobjektiin, eikä vain yhteen dag-solmuun.

mymodel = model(theta)

käynnissä MCMC analyysi

täsmennetään näytöt

meidän MCMC analyysi, meidän täytyy perustaa vektori monitorit tallentaa valtioiden meidän Markov ketjun. Monitorin kaikkia toimintoja kutsutaan nimellä mn*, missä * on yleismerkki, joka edustaa monitorin tyyppiä. Ensin alustamme mallinäytön käyttämällä mnModel – toimintoa. Tämä luo uuden monitor-muuttujan, joka tulostaa valtiot kaikille mallin parametreille, kun ne siirretään MCMC-funktioon.

monitors.append( mnModel(filename="output/simple_OU.log", printgen=10) )

luo lisäksi näyttömonitori, joka ilmoittaa määritettyjen muuttujien tilan näytölle arvolla mnScreen:

monitors.append( mnScreen(printgen=1000, sigma2, alpha, theta) )

alustetaan ja ajetaan MCMC-simulaatio

täysin määritellyllä mallilla, monitoreilla ja siirroilla, voimme nyt perustaa MCMC-algoritmin, joka ottaa näytteen parametriarvoista niiden posteriorisen todennäköisyyden mukaan. mcmc() funktio luo MCMC-oliomme:

mymcmc = mcmc(mymodel, monitors, moves, nruns=2, combine="mixed")

nyt, suorita MCMC:

mymcmc.run(generations=50000)

kun analyysi on valmis, sinulla on valvotut tiedostot ulostulohakemistossa.

⇨ Rev tiedosto tämän analyysin suorittamiseksi: mcmc_OU.Rev

OU-prosessissa kehittyvät merkit pyrkivät kohti stationaarista jakaumaa, joka on normaalijakauma keskiarvolla $\theta$ ja varianssi $\sigma^2 \div 2\alpha$. Siksi, jos kehitysnopeus on korkea (tai puun oksat ovat suhteellisen pitkiä), voi olla vaikea arvioida $\sigma^2$ ja $\alpha$ erikseen, koska ne molemmat määrittävät prosessin pitkän aikavälin varianssin. Voimme nähdä, vaikuttaako tämä analyysiimme tutkimalla muuttujien yhteistä posteriorijakaumaa Tracer. Kun parametrit ovat positiivisesti korreloivat, meidän pitäisi epäröidä tulkita niiden marginaalijakaumat (toisin sanoen, älä tee päätelmiä noin nopeus sopeutumista tai varianssi parametri erikseen).

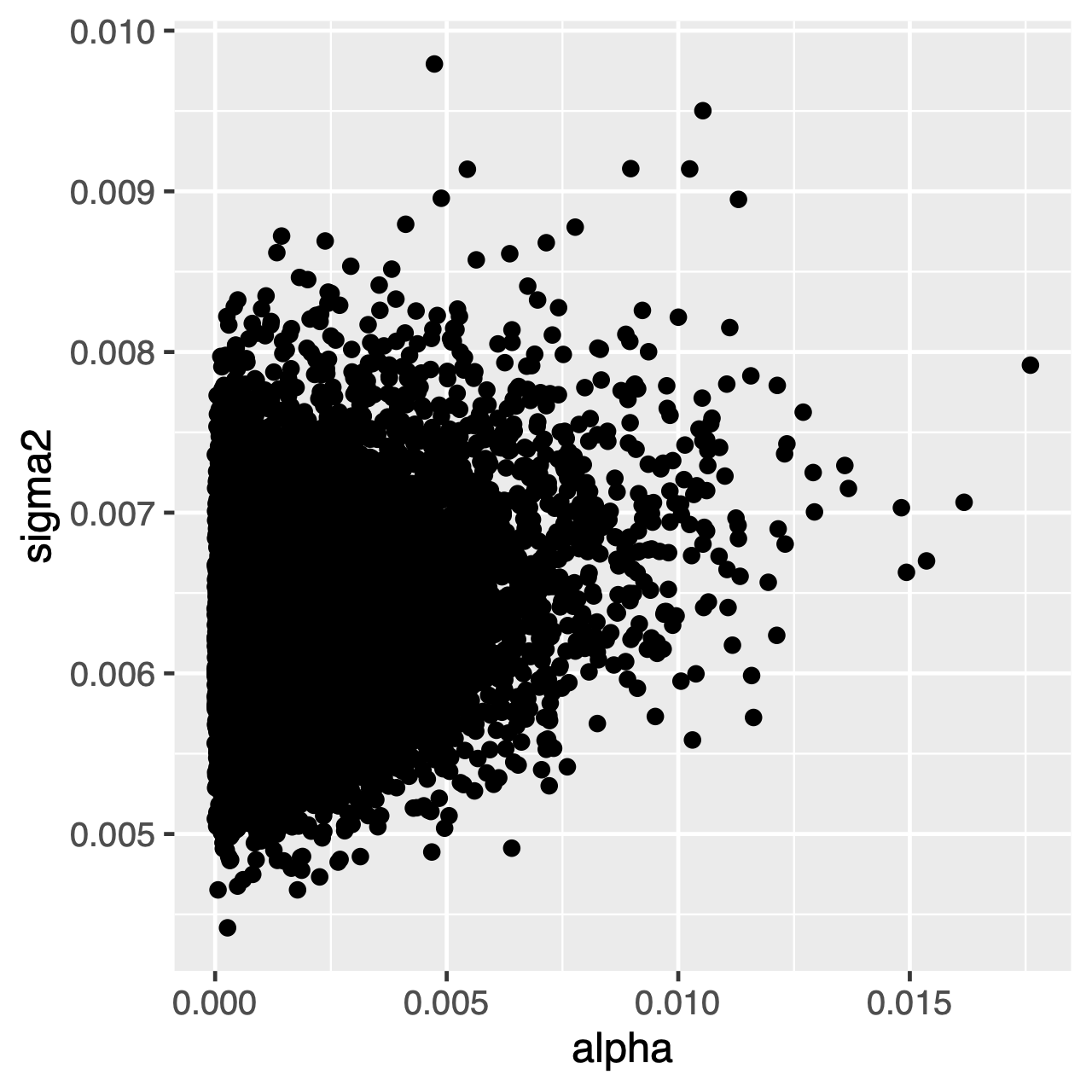
Harjoitus 1

• Suorita MCMC-simulaatio arvioidaksesi OU: n optimin posteriorijakauman (theta).
• Lataa luotu tulostustiedosto kohtaan Tracer: mikä on posteriorinen keskiarvo theta ja mikä on arvioitu HPD?
• käytä Tracer vertailemaan alpha ja sigma2yhteisiä posteriorisia jakaumia. Korreloivatko nämä parametrit vai eivät?
• vertaa edeltävää keskiarvoa posterioriseen keskiarvoon. (Vihje: Käytä valinnaista argumenttia underPrior=TRUE funktiossa mymcmc.run()) ovatko ne erilaisia (esim.,)? Onko posteriorinen keskiarvo edeltävän 95% todennäköisyysvälin ulkopuolella?

verrattaessa OU-ja BM-malleja

nyt kun saamme sekä BM-että OU-malleja, voimme luonnollisesti haluta tietää, kumpi malli sopii paremmin. Tässä osiossa opimme käyttämään palautuvaa Markovin ketjua Monte Carlo vertailemaan OU-ja BM-mallien istuvuutta.

Mallivalinta käyttäen Reversiibeliä hypyn MCMC

testataksemme hypoteesia, että hahmo kehittyy kohti valikoivaa optimia, kuvitellaan kaksi mallia. Ensimmäinen malli, jossa ei ole sopeutumista kohti optimaalista, on silloin, kun $\alpha = 0$. Toinen malli vastaa OU-mallia $ \alpha > 0$. Tämä toimii, koska Brownin liike on OU-mallin erikoistapaus, kun sopeutumisnopeus on 0. Valitettavasti, koska $\alpha$ on jatkuva parametrit, standardi Markovin ketju ei koskaan käy valtioissa, joissa jokainen arvo on täsmälleen sama kuin 0. Onneksi voimme käyttää käännettävää hyppyä, jotta Markovin ketju voi harkita vierailua Brownian-motion-malliin. Tämä edellyttää, että määritetään kunkin kahden mallin ennakkotodennäköisyys ja annetaan aiempi jakauma $\alpha$ OU-mallille.

Rjmcmc: n avulla Markovin ketju voi käydä kahdessa mallissa suhteessa niiden posterioriseen todennäköisyyteen. Mallin $i$ posteriorinen todennäköisyys on vain murto-osa näytteistä, joissa ketju vieraili kyseisessä mallissa. Koska määrittelemme myös mallien Priorin, voimme laskea Bayes-kertoimen OU-mallille seuraavasti:

\

missä $P (\text{OU model} \mid X)$ ja $P (\text{OU model})$ ovat ou-mallin posterior-todennäköisyys ja priori-todennäköisyys.

reversiibeli-hyppy OU-ja BM-mallien välillä

jotta rjMCMC voidaan ottaa käyttöön, on yksinkertaisesti asetettava palautuva-hyppy ennen kyseistä parametria, $\alpha$. Voimme muokata prioria alpha niin, että se ottaa joko vakion arvon 0, tai se piirretään edeltävästä jakaumasta. Lopuksi tarkennetaan ou: n mallille ennakkotodennäköisyys p = 0.5.

alpha ~ dnReversibleJumpMixture(0.0, dnExponential(10), 0.5)

tämän jälkeen annetaan alpha reversiibeli hyppyehdotus, jossa ehdotetaan muutoksia näiden kahden mallin välillä.

moves.append( mvRJSwitch(alpha, weight=1.0) )

lisäksi tarjoamme normaalin mvScale ehdotuksen siitä, milloin MCMC vierailee OU-mallissa.

moves.append( mvScale(alpha, weight=1.0) )

mukana on muuttuja, jonka arvo on 1, kun ketju vierailee OU-mallissa, ja vastaava muuttuja, jonka arvo on 1, kun se vierailee BM-mallissa. Näin voimme helposti laskea mallien posteriorisen todennäköisyyden, koska meidän on yksinkertaisesti laskettava tämän parametrin posteriorinen keskiarvo.

is_OU := ifelse(alpha != 0.0, 1, 0)is_BM := ifelse(alpha == 0.0, 1, 0)

näytteen murto-osa, jolle is_OU = 1 on OU-mallin posteriorinen todennäköisyys. Vaihtoehtoisesti tämän indikaattorimuuttujan posteriorinen keskiarvo vastaa ou-mallin posteriorista todennäköisyyttä. Näitä arvoja voidaan käyttää yllä olevassa Bayes-kertoimen yhtälössä laskemaan Bayes-kertoimen tuki kummallekin mallille.

1. Felsenstein J. 1985. Fylogeniat ja vertailumenetelmä. Amerikkalainen Luonnontieteilijä.:1-15.10.1086/284325
2. Höhna S., Heath T. A., Boussau B., Landis M. J., Ronquist F., Huelsenbeck J. P. 2014. Probabilistinen graafinen Malliesitys fylogenetiikassa. Systemaattinen Biologia. 63: 753-771. 10. 1093 / sysbio / syu039
3. Landis M. J., Schraiber J. G. 2017. Pulssimainen evoluutio muokkasi nykyaikaisia selkärankaisten kehon kokoja. Proceedings of the National Academy of Sciences. 114: 13224-13229. 10. 1073 / pnas.1710920114