Modèles Ornstein-Uhlenbeck simples

Estimation des Optima évolutifs

Ce tutoriel montre comment spécifier un modèle d’Ornstein-Uhlenbeck où le phénotype optimal est supposé constant parmi les branches d’une phylogénie étalonnée dans le temps (référence manquante) en utilisant les ensembles de données de (log) taille corporelle à travers les clades de vertébrés à partir de (référence manquante). Nous fournissons la représentation graphique probabiliste de chaque composant pour ce tutoriel. Après avoir spécifié le modèle, vous estimerez les paramètres de l’évolution d’Ornstein-Uhlenbeck à l’aide de la chaîne de Markov Monte Carlo (MCMC).

Modèle d’Ornstein-Uhlenbeck

Sous le modèle simple d’Ornstein-Uhlenbeck (OU), un caractère continu est supposé évoluer vers une valeur optimale, $\thêta$. Le caractère évolue de manière stochastique selon un paramètre de dérive,sig\sigma^2$. Le caractère est tiré vers l’optimum par le taux d’adaptation,alpha\alpha$; des valeurs alpha plus grandes indiquent que le caractère est tiré plus fortement vers $\thêta$. Lorsque le caractère s’éloigne deth\theta,, le paramètre\\alpha determines détermine la force avec laquelle le caractère est retiré. Pour cette raison, $\alpha is est parfois appelé paramètre « élastique ». Lorsque le paramètre de taux d’adaptation\\alpha = 0,, le modèle OU se réduit au modèle BM. Le modèle graphique résultant est assez simple, car la probabilité des caractères continus ne dépend que de la phylogénie (que nous supposons connue dans ce tutoriel) et des trois paramètres OU().

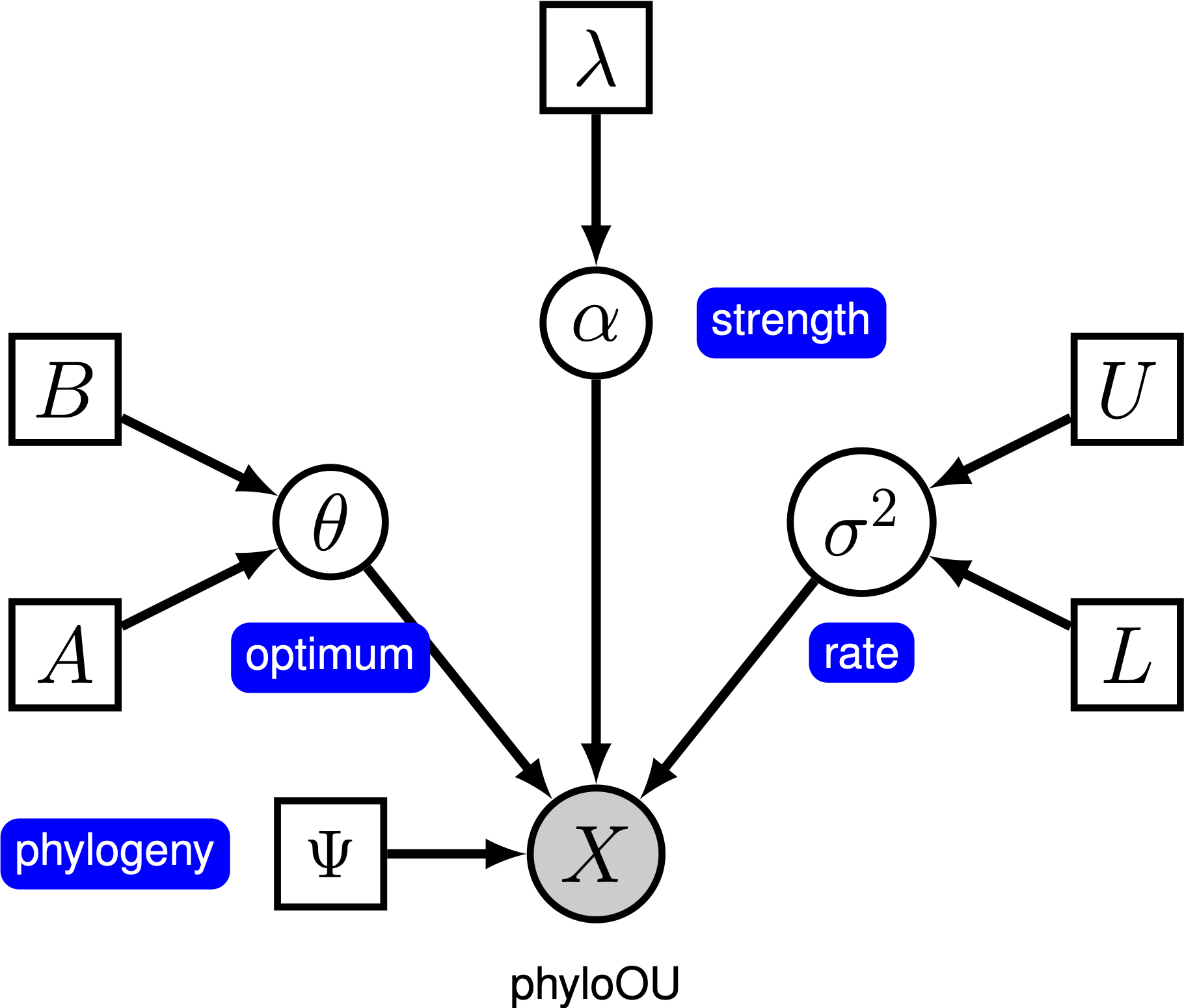
Dans ce tutoriel, nous utilisons les 66 ensembles de données sur les phylogénies des vertébrés et la taille corporelle (log) de (Landis et Schraiber 2017).

⇨ La spécification complète du modèle OU se trouve dans le fichier appelé mcmc_OU.Rev.

Lisez les données

Nous commençons par décider lequel des 66 ensembles de données de vertébrés utiliser. Ici, nous supposons que nous analysons le premier ensemble de données (Acanthuridae), mais vous devriez vous sentir libre de choisir l’un des ensembles de données.

dataset <- 1

Maintenant, nous lisons dans l’arbre (calibré dans le temps) correspondant à notre jeu de données choisi.

T <- readTrees("data/trees.nex")

Ensuite, nous lisons dans les données de caractères pour le même ensemble de données.

data <- readContinuousCharacterData("data/traits.nex")

De plus, nous initialisons une variable pour notre vecteur de déplacements et de moniteurs:

moves = VectorMoves()monitors = VectorMonitors()

Spécification du modèle

Modèle d’arbre

Dans ce tutoriel, nous supposons que l’arbre est connu sans zone. Nous créons un nœud constant pour l’arbre qui correspond à la phylogénie observée.

tree <- T

Paramètre de vitesse

Le taux d’évolution stochastique est contrôlé par le paramètre de vitesse, $\sigma^2$. Nous dessinons le paramètre de taux à partir d’un loguniforme antérieur. Ce précédent est uniforme sur l’échelle log, ce qui signifie qu’il représente une ignorance de l’ordre de grandeur du taux.

sigma2 ~ dnLoguniform(1e-3, 1)

Afin d’estimer la distribution postérieure desig\sigma ^2$, nous devons fournir un mécanisme de proposition MCMC qui fonctionne sur ce nœud. Parce quesig\sigma^2 is est un paramètre de débit, et doit donc être positif, nous utilisons un mouvement de mise à l’échelle appelé mvScale.

moves.append( mvScale(sigma2, weight=1.0) )

Paramètre d’adaptation

Le taux d’adaptation vers l’optimum est déterminé par le paramètrealpha\alpha$. Nous tirons $\alpha from d’une distribution antérieure exponentielle et y plaçons une proposition d’échelle.

alpha ~ dnExponential(10)moves.append( mvScale(alpha, weight=1.0) )

Optimum

Nous tirons la valeur optimale d’un uniforme vague allant de -10 à 10 (vous devez changer cela avant si votre personnage est en dehors de cette plage). Parce que ce paramètre peut être positif ou négatif, nous utilisons un mouvement de diapositive pour proposer des modifications pendant MCMC.

theta ~ dnUniform(-10, 10)moves.append( mvSlide(theta, weight=1.0) )

Modèle d’Ornstein-Uhlenbeck

Maintenant que nous avons spécifié les paramètres du modèle, nous pouvons tirer les données de caractères du modèle phylogénétique OU correspondant. Dans cet exemple, nous utilisons l’algorithme REML pour calculer efficacement la probabilité (Felsenstein 1985). Nous supposons que le caractère commence à la valeur optimale à la racine de l’arbre.

X ~ dnPhyloOrnsteinUhlenbeckREML(tree, alpha, theta, sigma2^0.5, rootStates=theta)

Notant queXX is est la donnée observée (), nous fixons le data à ce nœud stochastique.

X.clamp(data)

Enfin, nous créons un objet workspace pour l’ensemble du modèle avec model(). Rappelons que les objets workspace sont initialisés avec l’opérateur = et ne font pas eux-mêmes partie du modèle graphique bayésien. La fonction model() parcourt tout le graphique du modèle et trouve tous les nœuds du modèle que nous avons spécifiés. Cet objet fournit un moyen pratique de se référer à l’objet modèle entier, plutôt qu’à un seul nœud DAG.

mymodel = model(theta)

Exécution d’une analyse MCMC

Spécification des moniteurs

Pour notre analyse MCMC, nous devons configurer un vecteur de moniteurs pour enregistrer les états de notre chaîne de Markov. Les fonctions de moniteur sont toutes appelées mn*, où * est le caractère générique représentant le type de moniteur. Tout d’abord, nous initialiserons le moniteur de modèle en utilisant la fonction mnModel. Cela crée une nouvelle variable de surveillance qui affichera les états de tous les paramètres du modèle lorsqu’elle sera transmise à une fonction MCMC.

monitors.append( mnModel(filename="output/simple_OU.log", printgen=10) )

De plus, créez un moniteur d’écran qui rapportera les états des variables spécifiées à l’écran avec mnScreen:

monitors.append( mnScreen(printgen=1000, sigma2, alpha, theta) )

Initialisant et exécutant la simulation MCMC

Avec un modèle entièrement spécifié, un ensemble de moniteurs et un ensemble de mouvements, nous pouvons maintenant configurer l’algorithme MCMC qui échantillonnera les valeurs de paramètres en fonction de leur probabilité postérieure. La fonction mcmc() créera notre objet MCMC:

mymcmc = mcmc(mymodel, monitors, moves, nruns=2, combine="mixed")

Maintenant, exécutez le MCMC:

mymcmc.run(generations=50000)

Une fois l’analyse terminée, vous aurez les fichiers surveillés dans le répertoire youroutput.

file Le fichier Rev pour effectuer cette analyse: mcmc_OU.Rev

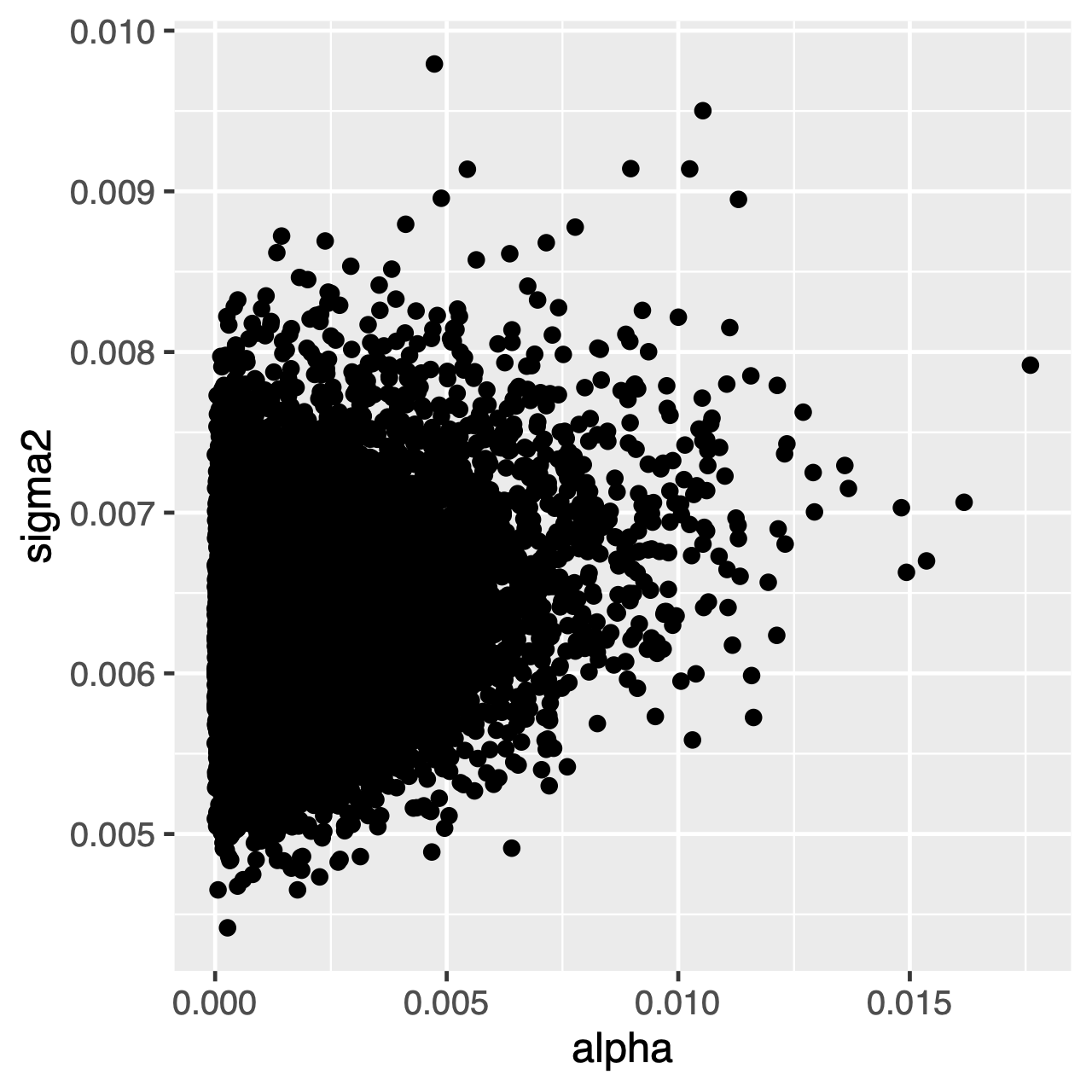
Les caractères évoluant sous le processus OU tendront vers une distribution stationnaire, qui est une distribution normale avec la moyenne\\thêta and et la variance\\sigma^2\div 2\alpha$. Par conséquent, si les taux d’évolution sont élevés (ou si les branches de l’arbre sont relativement longues), il peut être difficile d’estimer separately\sigma^22 et $\alpha separately séparément, car ils déterminent tous deux la variance à long terme du processus. Nous pouvons voir si cela affecte notre analyse en examinant la distribution postérieure articulaire des paramètres dans Tracer. Lorsque les paramètres sont corrélés positivement, nous devrions hésiter à interpréter leurs distributions marginales (c’est-à-dire à ne pas faire d’inférences sur le taux d’adaptation ou le paramètre de variance séparément).

Exercice 1

• Exécutez une simulation MCMC pour estimer la distribution postérieure de l’optimum OU (theta).
• Chargez le fichier de sortie généré dans Tracer: Quelle est l’estimation postérieure moyenne de theta et quelle est la HPD estimée?
• Utilisez Tracer pour comparer les distributions postérieures articulaires de alpha et sigma2. Ces paramètres sont-ils corrélés ou non ?
• Comparez la moyenne antérieure à la moyenne postérieure. (Astuce: Utilisez l’argument optionnel underPrior=TRUE dans la fonction mymcmc.run()) Sont-ils différents (par exemple,)? La moyenne postérieure est-elle en dehors de l’intervalle de probabilité précédent de 95%?

Comparaison des modèles OU et BM

Maintenant que nous pouvons adapter les modèles BM et OU, nous pourrions naturellement vouloir savoir quel modèle convient le mieux. Dans cette section, nous allons apprendre à utiliser la chaîne Markov à saut réversible Monte Carlo pour comparer l’ajustement des modèles OU et BM.

Sélection de modèle à l’aide du MCMC à saut réversible

Pour tester l’hypothèse qu’un caractère évolue vers un optimum sélectif, nous imaginons deux modèles. Le premier modèle, où il n’y a pas d’adaptation vers l’optimum, est le cas où $\alpha = 0$. Le deuxième modèle correspond au modèle OU avec $\alpha > 0$. Cela fonctionne car le mouvement brownien est un cas particulier du modèle OU lorsque le taux d’adaptation est de 0. Malheureusement, commealpha\alpha is est un paramètre continu, une chaîne de Markov standard ne visitera jamais les états où chaque valeur est exactement égale à 0. Heureusement, nous pouvons utiliser le saut réversible pour permettre à la chaîne de Markov d’envisager de visiter le modèle de mouvement brownien. Cela implique de spécifier la probabilité préalable sur chacun des deux modèles et de fournir la distribution préalable pour $\alpha for pour le modèle OU.

L’utilisation de rjMCMC permet à la chaîne de Markov de visiter les deux modèles proportionnellement à leur probabilité postérieure. La probabilité postérieure du modèleii is est simplement la fraction d’échantillons où la chaîne visitait ce modèle. Comme nous spécifions également un prior sur les modèles, nous pouvons calculer un facteur de Bayes pour le modèle OU comme suit:

\

oùPP(\text{OU model}\mid X) and etPP(\text{OU model}) are sont respectivement la probabilité postérieure et la probabilité antérieure du modèle OU.

Saut réversible entre les modèles OU et BM

Pour activer rjMCMC, il suffit de placer un saut réversible au préalable sur le paramètre pertinent,\\alpha$. Nous pouvons modifier le prior on alpha pour qu’il prenne soit une valeur constante de 0, soit qu’il soit tiré d’une distribution prior. Enfin, nous spécifions une probabilité préalable sur le modèle OU de p = 0.5.

alpha ~ dnReversibleJumpMixture(0.0, dnExponential(10), 0.5)

Nous fournissons ensuite une proposition de saut réversible sur alpha qui propose des changements entre les deux modèles.

moves.append( mvRJSwitch(alpha, weight=1.0) )

De plus, nous fournissons la proposition normale mvScale lorsque le MCMC visite le modèle d’unité d’organisation.

moves.append( mvScale(alpha, weight=1.0) )

Nous incluons une variable qui a une valeur 1 lorsque la chaîne visite le modèle OU, et une variable correspondante qui a une valeur 1 lorsqu’elle visite le modèle BM. Cela nous permettra de calculer facilement la probabilité postérieure des modèles car il nous suffit de calculer la valeur moyenne postérieure de ce paramètre.

is_OU := ifelse(alpha != 0.0, 1, 0)is_BM := ifelse(alpha == 0.0, 1, 0)

La fraction d’échantillons pour laquelle is_OU = 1 est la probabilité postérieure du modèle OU. Alternativement, l’estimation moyenne postérieure de cette variable indicatrice correspond à la probabilité postérieure du modèle OU. Ces valeurs peuvent être utilisées dans l’équation du facteur de Bayes ci-dessus pour calculer la prise en charge du facteur de Bayes pour l’un ou l’autre modèle.

1. Felsenstein J. 1985. Phylogénies et méthode comparative. Le naturaliste américain.:1-15.10.1086/284325
2. Höhna S., Heath T.A., Boussau B., Landis M.J., Ronquist F., Huelsenbeck J.P. 2014. Représentation de Modèles Graphiques Probabilistes en Phylogénétique. Biologie systématique. 63:753-771.10.1093/sysbio/syu039
3. Landis M.J., Schraiber J.G. 2017. L’évolution pulsée a façonné la taille du corps des vertébrés modernes. Actes de l’Académie nationale des Sciences. 114:13224-13229.10.1073/pnas.1710920114