egyszerű Ornstein-Uhlenbeck modellek

az evolúciós Optima becslése

ez az oktatóanyag bemutatja, hogyan lehet meghatározni egy Ornstein-Uhlenbeck modellt, ahol feltételezzük, hogy az optimális fenotípus állandó az időben kalibrált filogenitás (hiányzó referencia) ágai között a gerinces kládok (hiányzó referencia) (log) testméretének adatkészletei felhasználásával. Az oktatóanyag minden egyes összetevőjének valószínűségi grafikus modell-ábrázolását biztosítjuk. A modell megadása után megbecsülheti az Ornstein-Uhlenbeck evolúció paramétereit a Markov chain Monte Carlo (MCMC) segítségével.

Ornstein-Uhlenbeck modell

az egyszerű Ornstein-Uhlenbeck (OU) modell alatt feltételezzük, hogy a folytonos karakter az optimális érték, a $\theta$felé fejlődik. A karakter sztochasztikusan fejlődik egy drift paraméter szerint, $ \ sigma^2$. A karaktert az optimális felé húzza az alkalmazkodási sebesség, $ \ alpha$; az alfa nagyobb értékei azt jelzik, hogy a karakter erősebben húzódik a $\theta$felé. Amint a karakter elmozdul a $\theta$ – tól, a $\alpha$ paraméter határozza meg, hogy a karakter milyen erősen visszahúzódik. Emiatt a $ \ alpha$ – t néha “gumiszalag” paraméternek nevezik. Amikor a $\alpha = 0$ adaptációs paraméter sebessége, az OU modell összeomlik a BM modellre. Az így kapott grafikus modell meglehetősen egyszerű, mivel a folytonos karakterek valószínűsége csak a filogenitástól függ (amiről feltételezzük, hogy ismert ebben az oktatóanyagban) és a három OU paramétertől ().

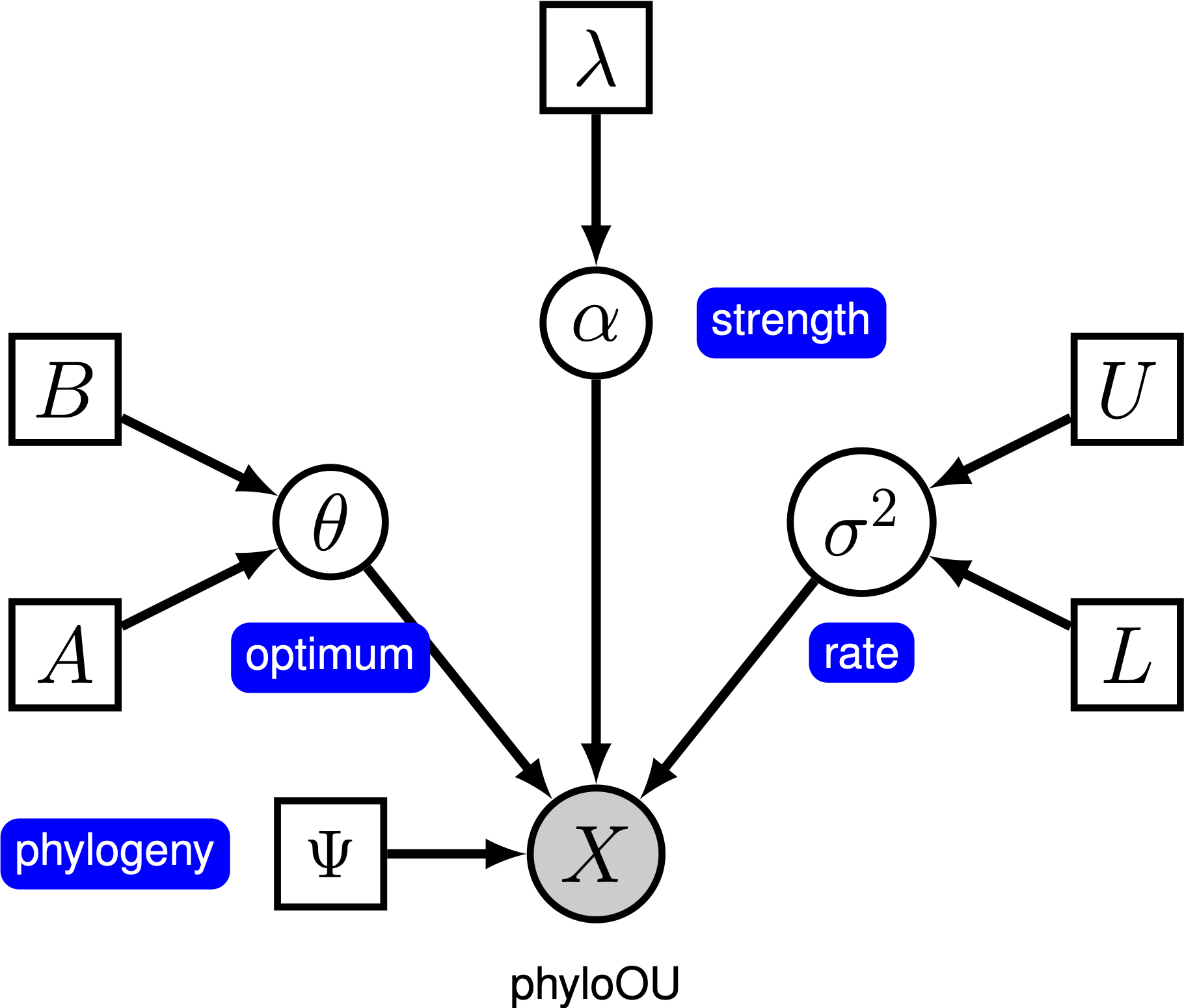
ebben az oktatóanyagban a 66 gerinces törzsfejlődést és (log) testméret-adatkészletet használjuk (Landis and Schraiber 2017).

a teljes OU-modell specifikáció a mcmc_OU.Rev nevű fájlban található.

olvassa el az adatokat

először eldöntjük, hogy a 66 gerinces adatkészlet közül melyiket használjuk. Itt feltételezzük, hogy az első adatkészletet (Acanthuridae) elemezzük, de nyugodtan válasszon bármelyik adatkészletet.

dataset <- 1

most a választott adatkészletünknek megfelelő (időben kalibrált) fában olvasunk.

T <- readTrees("data/trees.nex")

ezután ugyanazon adatkészlet karakteradatait olvassuk el.

data <- readContinuousCharacterData("data/traits.nex")

ezenkívül inicializálunk egy változót a vektorunkhoz ofmoves és monitorok:

moves = VectorMoves()monitors = VectorMonitors()

a modell megadása

fa modell

ebben az oktatóanyagban feltételezzük, hogy a fa terület nélkül ismert. Létrehozunk egy állandó csomópontot a fa számára, amely megfelel a megfigyelt filogenitásnak.

tree <- T

Rate paraméter

az evolúció sztochasztikus sebességét a rate paraméter, $\sigma^2$szabályozza. A rate paramétert egy logból rajzoljukegységes prior. Ez a prior egységes a log skálán, ami azt jelenti, hogy az jelentése tudatlanság az arány nagyságrendjével kapcsolatban.

sigma2 ~ dnLoguniform(1e-3, 1)

annak érdekében, hogy megbecsüljük a $\sigma^2$ hátsó eloszlását, meg kell adnunk egy MCMC javaslat mechanizmust, amely ezen a csomóponton működik. Mivel a $ \ sigma^2$ egy rate paraméter, és ezért pozitívnak kell lennie, egy mvScalenevű skálázási lépést használunk.

moves.append( mvScale(sigma2, weight=1.0) )

adaptációs paraméter

az optimális adaptáció sebességét a $\alpha$paraméter határozza meg. A $\alpha$ – t egy exponenciális előzetes eloszlásból húzzuk ki, és egy skálajavaslatot helyezünk rá.

alpha ~ dnExponential(10)moves.append( mvScale(alpha, weight=1.0) )

Optimum

az optimális értéket egy homályos egységes prior-tól -10-től 10-ig terjedő értékből vonjuk le (ezt a priort meg kell változtatnod, ha a karaktered kívül esik ezen a tartományon). Mivel ez a paraméter lehet pozitív vagy negatív, egy dia mozdulattal javasolunk változtatásokat az MCMC során.

theta ~ dnUniform(-10, 10)moves.append( mvSlide(theta, weight=1.0) )

Ornstein-Uhlenbeck modell

most, hogy megadtuk a modell paramétereit, levonhatjuk a karakteradatokat a megfelelő filogenetikai OU modellből. Ebben a példában a reml algoritmust használjuk a valószínűség hatékony kiszámításához (Felsenstein 1985). Feltételezzük, hogy a karakter az optimális értéknél kezdődik a fa gyökerénél.

X ~ dnPhyloOrnsteinUhlenbeckREML(tree, alpha, theta, sigma2^0.5, rootStates=theta)

megjegyezve, hogy $X$ a megfigyelt adat (), a data – ot ehhez a sztochasztikus csomóponthoz rögzítjük.

X.clamp(data)

végül létrehozunk egy munkaterület-objektumot a teljes modellhez model() – vel. Ne feledje, hogy a munkaterület objektumok inicializálása a = operátorral történik, és maguk nem részei a Bayes-féle grafikus modellnek. A model() függvény bejárja a teljes modellgráfot, és megkeresi a megadott modell összes csomópontját. Ez az objektum kényelmes módot nyújt a teljes modellobjektumra való hivatkozásra, nem csak egyetlen DAG csomópontra.

mymodel = model(theta)

MCMC analízis futtatása

monitorok meghatározása

MCMC elemzésünkhöz be kell állítanunk egy monitorvektort a Markov-lánc állapotainak rögzítésére. A monitor funkciók mindegyike mn*, ahol * a helyettesítő karakter, amely a monitor típusát képviseli. Először inicializáljuk a modellmonitort a mnModel funkcióval. Ez létrehoz egy új monitor változót, amely kiadja az összes modellparaméter állapotát, amikor átkerül egy MCMC függvénybe.

monitors.append( mnModel(filename="output/simple_OU.log", printgen=10) )

ezenkívül hozzon létre egy képernyőmonitort, amely a megadott változók állapotát mnScreen:

monitors.append( mnScreen(printgen=1000, sigma2, alpha, theta) )

az MCMC szimuláció inicializálása és futtatása

egy teljesen meghatározott modellel, egy monitorkészlettel és egy sor mozdulattal, a wecan Most beállíthatja az MCMC algoritmust, amely a paraméterértékeket a hátsó valószínűségük arányában fogja mintavételezni. A mcmc() függvény létrehozza az MCMC objektumunkat:

mymcmc = mcmc(mymodel, monitors, moves, nruns=2, combine="mixed")

most futtassa az MCMC-t:

mymcmc.run(generations=50000)

amikor az elemzés befejeződött, a megfigyelt fájlok a sajátban lesznek.kimeneti könyvtár.

a Rev fájl ezen elemzés elvégzéséhez: mcmc_OU.Rev

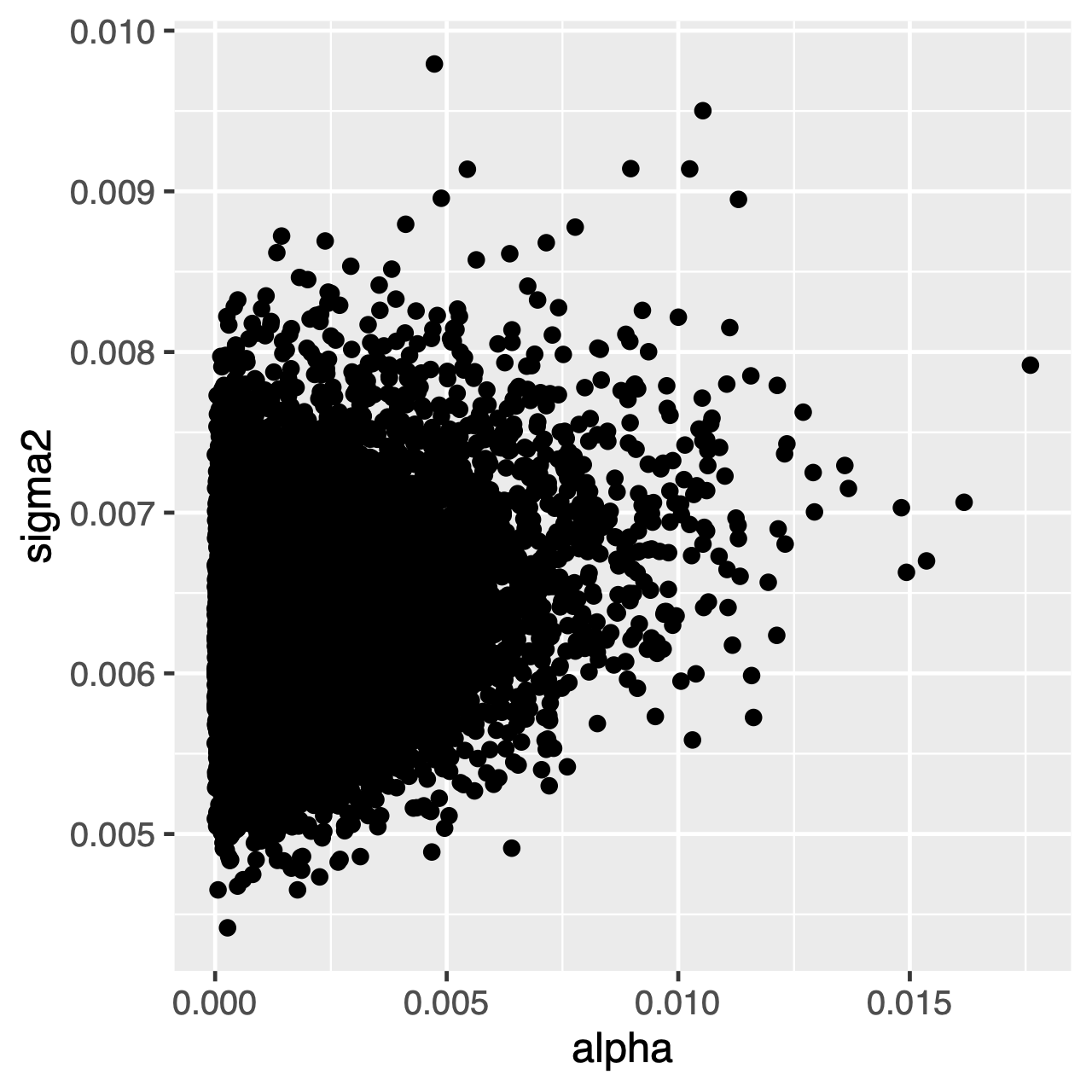
az OU folyamat során kialakuló karakterek egy stacionárius Eloszlás felé hajlanak, amely normális eloszlás átlagos $\theta$ és variancia $\sigma^2 \div 2\alpha$. Ezért, ha az evolúció sebessége magas (vagy a fa ágai viszonylag hosszúak), nehéz lehet külön megbecsülni a $\sigma^2$ és a $\alpha$ értéket, mivel mindkettő meghatározza a folyamat hosszú távú varianciáját. Láthatjuk, hogy ez befolyásolja-e elemzésünket a paraméterek közös hátsó eloszlásának vizsgálatával Tracer. Ha a paraméterek pozitívan korrelálnak, haboznunk kell értelmezni marginális eloszlásaikat (vagyis ne tegyünk külön következtetéseket az adaptáció sebességéről vagy a variancia paraméterről).

gyakorlat 1

• futtasson egy MCMC szimulációt az OU optimális hátsó eloszlásának becsléséhez (theta).
• töltse be a generált kimeneti fájlt Tracer: mi az átlagos hátsó becslés theta és mi a becsült HPD?
• a Tracer használatával hasonlítsa össze a alphaés a sigma2 közös hátsó eloszlását. Ezek a paraméterek korreláltak vagy korrelálatlanok?
• hasonlítsa össze az előző átlagot a hátsó átlaggal. (Tipp: Használja a underPrior=TRUE opcionális argumentumot a mymcmc.run() függvényben) különböznek egymástól (pl. )? A hátsó átlag az előző 95% – os valószínűségi intervallumon kívül van?

az OU és a BM modellek összehasonlítása

most, hogy mind a BM, mind az OU modellekhez illeszkedhetünk, természetesen érdemes tudni, hogy melyik modell jobban illeszkedik. Ebben a részben megtanuljuk, hogyan kell használni a reverzibilis Ugrás Markov lánc Monte Carlo összehasonlítani a fit OU és BM modellek.

Modellválasztás reverzibilis ugrással MCMC

annak a hipotézisnek a teszteléséhez, hogy egy karakter szelektív optimum felé fejlődik, két modellt képzelünk el. Az első modell, ahol nincs adaptáció az optimum felé, az az eset, amikor $ \ alpha = 0$. A második modell megfelel az OU modellnek $\alpha > 0$értékkel. Ez azért működik, mert a Brown-mozgás az OU modell speciális esete, amikor az alkalmazkodás sebessége 0. Sajnos, mivel a $ \ alpha$ egy folyamatos paraméter, egy szabványos Markov-lánc soha nem fog meglátogatni olyan államokat,ahol minden érték pontosan 0. Szerencsére használhatjuk a reverzibilis ugrást, hogy a Markov-lánc fontolóra vegye a Brown-mozgás modell meglátogatását. Ez magában foglalja a két modell előzetes valószínűségének megadását, valamint a $\alpha$ előzetes eloszlásának megadását az OU modellhez.

az rjMCMC használata lehetővé teszi a Markov-lánc számára, hogy meglátogassa a két modellt a hátsó valószínűségük arányában. A $i$ modell hátsó valószínűsége egyszerűen a minták töredéke, ahol a lánc meglátogatta ezt a modellt. Mivel a modelleken priort is megadunk, az OU modell Bayes-tényezőjét a következőképpen számíthatjuk ki:

\

ahol $P( \text{OU model} \mid X)$ és $P( \text{OU model})$ az OU modell posterior és prior valószínűsége.

reverzibilis ugrás OU és BM modellek között

az rjMCMC engedélyezéséhez egyszerűen egy reverzibilis ugrást kell elhelyeznünk a megfelelő paraméter, $\alpha$előtt. Módosíthatjuk a prior-t alpha úgy, hogy vagy 0 állandó értéket vegyen fel, vagy egy korábbi eloszlásból származik. Végül megadunk egy előzetes valószínűséget az OU modellen p = 0.5.

alpha ~ dnReversibleJumpMixture(0.0, dnExponential(10), 0.5)

ezután egy reverzibilis ugrási javaslatot nyújtunk be alpha, amely változtatásokat javasol a két modell között.

moves.append( mvRJSwitch(alpha, weight=1.0) )

ezenkívül megadjuk a normál mvScale javaslatot arra az esetre, amikor az MCMC meglátogatja az OU modellt.

moves.append( mvScale(alpha, weight=1.0) )

tartalmaz egy változót, amelynek értéke 1, amikor a lánc az OU modellt látogatja, és egy megfelelő változót, amelynek értéke 1, amikor a BM modellt látogatja. Ez lehetővé teszi számunkra, hogy könnyen kiszámítsuk a modellek hátsó valószínűségét, mert egyszerűen ki kell számolnunk ennek a paraméternek a hátsó középértékét.

is_OU := ifelse(alpha != 0.0, 1, 0)is_BM := ifelse(alpha == 0.0, 1, 0)

a minták azon hányada, amelyeknél is_OU = 1 az OU modell hátsó valószínűsége. Alternatív megoldásként ennek a mutatóváltozónak a hátsó átlagos becslése megfelel az OU modell hátsó valószínűségének. Ezek az értékek felhasználhatók a fenti Bayes-faktor egyenletben bármelyik modell Bayes-faktor támogatásának kiszámításához.

1. Felsenstein J. 1985. Filogenetika és az összehasonlító módszer. Az Amerikai Természettudós.:1-15.10.1086/284325
2. D. O., D. O., D. O., D. O., D. O., D. O., D. O., D. O., D. O., D. O., D. O., D. O., D. O., D. O., D. O. 2014. Valószínűségi grafikus Modellábrázolás a Filogenetikában. Szisztematikus Biológia. 63: 753-771. 10.1093/sysbio / syu039
3. Landis M. J., Schraiber J. G. 2017. Pulzáló evolúció alakú modern gerinces testméretek. A Nemzeti Tudományos Akadémia Közleményei. 114: 13224-13229.10. 1073 / pnas.1710920114