Riemann Tensor

a Riemann-tenzor(Schutz 1985) , más néven Riemann-Christoffel görbületi tenzor (Weinberg 1972, 133. o.; Arfken 1985, 123.o.) vagy Riemann görbületi tenzor (Misner et al. 1973, 218. O.), egy négyindexes tenzor, amely hasznos az Általános relativitáselméletben. Egyéb fontos általános relativisztikus tenzorok, így a Ricci görbület tenzor és skaláris görbület meghatározható kifejezéssel.

a Riemann-tenzor bizonyos értelemben az egyetlen tenzor, amely a metrikus tenzorból és annak első és második deriváltjából építhető fel,

(1)

ahol az első típusú Christoffel szimbólumok, vessző származék (Schmutzer 1968, 108. o.; Weinberg 1972). Az egyik dimenzióban . Négy dimenzióban 256 alkatrész van. A szimmetria kapcsolatok kihasználása,

(2)

a független komponensek száma 36-ra csökken. A feltétel használata

(3)

a koordináták száma 21-re csökken. Végül a

(4)

20 független komponensek maradnak (Misner et al. 1973, 220-221. o.; Arfken 1985, 123-124.o.).

általában a független komponensek számát méretekben a következők adják meg

(5)

a “négydimenziós piramis számok”, amelyek első néhány értéke 0, 1, 6, 20, 50, 105, 196, 336, 540, 825, … (OEIS A002415). A és – ból felépíthető skalárok száma

(6)

(Weinberg 1972). Az első néhány érték Akkor 0, 1, 3, 14, 40, 90, 175, 308, 504,780, … (OEIS A050297).

a Jacobi tenzor szempontjából ,

(7)

legyen

(8)

ahol a belsejében lévő mennyiség a második fajta Christoffel szimbólum. Akkor

(9)

legegyszerűbb bomlására bontva dimenziókban,

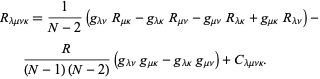(10)

itt a Ricci görbületi tenzor, a skaláris görbület, és a Weyl-tenzor.