INTRODUCCIÓN
Los riesgos competitivos (RC) han sido reconocidos como un caso especial de análisis del tiempo hasta el evento desde el siglo XVIII. Ocasionalmente se ha publicado trabajo en el área estadística o matemática incorporando nuevos desarrollos, incluida la monografía de David y Moeschberger.1 A medida que los datos se hicieron más extensos, claros y precisos con respecto a los diferentes tipos de resultados, la RC resurgió como un tipo crucial de análisis dentro del análisis del tiempo hasta el evento, necesario para una mejor comprensión de una enfermedad. Era necesario establecer la conexión entre los resultados matemáticos y el campo aplicado. Varios autores han contribuido para la comprensión de las situaciones de RC.2, 3 Otros autores mejoraron y desarrollaron técnicas y, en algunos casos, pusieron a disposición códigos informáticos listos para usar para las estadísticas aplicadas.4, 5, 6
INTRODUCCIÓN AL ANÁLISIS DEL TIEMPO HASTA EL EVENTO
En muchos estudios el resultado se observa longitudinalmente. De esta manera, se observa a todos los sujetos de la cohorte durante un período de tiempo hasta que ocurre el evento. Por ejemplo, el evento de interés puede ser la muerte, el ataque cardíaco o la recurrencia del cáncer. Los objetivos del estudio pueden ser estimar la probabilidad de ocurrencia del evento o su asociación con covariables de interés como el tratamiento o las características del sujeto. El análisis estadístico empleado se denomina análisis del tiempo hasta el evento o, a veces, análisis de supervivencia. El método más común para estimar la probabilidad de un evento es un enfoque no paramétrico comúnmente llamado Kaplan-Meier7 (KM) o método de límite de producto. El supuesto principal de la estimación de KM para la supervivencia es que las observaciones censuradas experimentarán el evento si se siguen el tiempo suficiente.
Para el resto de este artículo, se darán las probabilidades para el evento en lugar de la probabilidad para el evento libre. Por ejemplo, en lugar de probabilidad de supervivencia, se presentará probabilidad de muerte, que se puede estimar utilizando el complemento del estimador KM: 1-km.
INTRODUCCIÓN A LOS RIESGOS COMPETITIVOS
No es raro que un participante en un estudio experimente más de un tipo de evento. Una situación de RC ocurre cuando la ocurrencia de un tipo de evento cambia la capacidad de observar el evento de interés. Miyasaka et al.8 se realizó un estudio en una cohorte comunitaria de pacientes diagnosticados de fibrilación auricular entre 1986 y 2000 en el condado de Olmsted, Minnesota, Estados Unidos. El resultado primario fue la aparición de demencia. La mediana de seguimiento fue de 4,6 años. Otros tipos de eventos fueron accidente cerebrovascular y muerte. De los 2.837 individuos con fibrilación auricular, 299 tenían demencia y 1.638 murieron en el momento del análisis. Los números con accidente cerebrovascular no se reportan y se censuran en el análisis. La conclusión del estudio fue que la incidencia de demencia entre los individuos con fibrilación auricular es común (10,5% a los 5 años utilizando el método KM). La aparición de un accidente cerebrovascular antes de la demencia no afecta la observación de la demencia y, por lo tanto, no es un evento de RC. Por el bien de la discusión, ignoramos el hecho de que los accidentes cerebrovasculares múltiples pueden causar demencia. Por otro lado, una muerte sin demencia previa hace que la observación de la demencia sea imposible. Por lo tanto, una muerte sin demencia es un evento de RC para el punto final de la demencia. Además, una lesión grave en la cabeza podría considerarse un evento de RC, ya que los cambios de comportamiento del paciente podrían hacer imposible el diagnóstico de demencia.
Una situación de RC más sutil ocurre en el estudio realizado por Whalley et al.9 de la importancia de la ecocardiografía. Esta cohorte de 228 pacientes ancianos sintomáticos se sometió a ecocardiografía y fue seguida para hospitalización cardiovascular o muerte cardiovascular. La hipótesis fue que las características de la ecocardiografía predicen el evento cardiovascular. El resultado principal se definió como la medida compuesta que incluía muerte y/o hospitalización por causas cardiovasculares. Para este tipo de desenlace, una muerte por causas distintas de la enfermedad cardiovascular es un evento de RC y, como tal, un paciente ya no tiene riesgo de tener ninguno de los eventos de interés.
Se realizó un ensayo aleatorizado de 3 grupos, doble ciego, que abarcó 931 centros y 24 países para probar el efecto de valsartán vs valsartán+captopril vs captopril solo (VALIANT)10 sobre la mortalidad por cualquier causa. En total, 14 703 pacientes postinfarto de miocardio con disfunción del ventrículo izquierdo y/o insuficiencia cardíaca acumularon 1:1:1 en los 3 grupos. Dado que cualquier muerte se consideró un evento, este tipo de desenlace no tiene RC. El estudio apoyó la hipótesis de que la supervivencia en los 3 brazos era diferente. Sin embargo, el sangrado gastrointestinal (GI) se identificó como un efecto secundario grave en los 3 brazos. Moukarbel et al.11 estudiaron los posibles factores que podrían predecir el sangrado gastrointestinal. Para este criterio de valoración, la muerte sin hemorragia gastrointestinal es una RC clara.
Un número creciente de investigadores reconoce la presencia de RC y la necesidad de aplicar técnicas adecuadas. Núñez et al estudiaron una cohorte de 972 pacientes con síndrome coronario agudo sin elevación del segmento ST entre 2001 y 2005.12 Uno de los objetivos del estudio fue encontrar factores asociados a la rehospitalización por insuficiencia cardíaca aguda. Entre los factores estudiados se encontraban diabetes, antecedentes de cardiopatía isquémica, insuficiencia renal crónica, antecedentes de tabaquismo y antecedentes de tratamiento. Los autores reconocieron la posibilidad de RC, como la muerte antes de la rehospitalización, y aplicaron correctamente técnicas específicas para explicar la situación de RC.
Melberg et al.13 estudió una cohorte de 1.234 pacientes con enfermedad arterial coronaria sintomática que recibieron 2 tipos de tratamientos: injerto de revascularización coronaria (n = 594) o intervención coronaria percutánea (n = 640). De las 301 muertes observadas durante el seguimiento, el 42,5% fueron muertes cardiacas y el resto no cardiacas. Los autores presentan resultados para la mortalidad por todas las causas, así como para la mortalidad cardíaca y la mortalidad no cardíaca. Señalan que el porcentaje de mortalidad por todas las causas es la suma del porcentaje de mortalidad cardiaca y no cardiaca correctamente estimado teniendo en cuenta la RC. Los autores enfatizan la importancia de analizar cada uno de los eventos de interés en lugar de combinarlos en una mortalidad general. Este tema también es expuesto a un nivel más general por Mell y Jeong.14
Como se podría deducir de los ejemplos anteriores, la pregunta principal cuando hay presencia de RC es si ignorar la RC y censurar las observaciones que involucran RC o dar cuenta de la RC. Cuando se ignoran las RC y se censuran las observaciones de RC, el análisis se reduce a un escenario de tiempo hasta el evento «habitual». Debido a la familiaridad de este tipo de análisis y la disponibilidad de software, muchos investigadores recurren a este enfoque, como se ve en los ejemplos anteriores. Sin embargo, no solo los estadísticos2, 15, 16, 17, 18 coinciden unánimemente en que la estimación de la probabilidad de evento en este caso sobrestima la probabilidad verdadera. La siguiente pregunta natural es si el modelado se puede realizar dentro de estos límites (ignorar/censurar CR). Esto es más ambiguo y más difícil de comprender. Si bien tal análisis puede no carecer de valor, su interpretación casi siempre está plagada de dificultades. El requisito principal es que el evento CR (cuyas observaciones fueron censuradas y mezcladas con las observaciones censuradas verdaderas) debe ser independiente del evento de interés. Si este es el caso, entonces los resultados podrían interpretarse como el efecto de las covariables cuando los eventos de RC no existían. Sin embargo, esta suposición generalmente no se puede hacer y no se puede verificar o probar. En conclusión, cada vez que se censuran las observaciones de RC, la estimación de la probabilidad de evento es incorrecta y la interpretación del efecto de las covariables no es clara debido al desconocimiento de la independencia entre el evento de interés y el evento de RC.
Cuando el análisis se realiza teniendo en cuenta el CR (y codificado de forma distinta del evento de interés o la censura), la probabilidad se estima correctamente y el modelado tiene una interpretación directa. No hay ninguna presunción de independencia que obstaculice la interpretación. El coeficiente de una covariable así estimada representa el efecto de esa covariable sobre las probabilidades observadas.
Varios autores19, 20 intentaron comparar los dos enfoques en términos de la potencia de las pruebas utilizando simulaciones. Sin embargo, el investigador debe ser consciente de que el principal problema está en la interpretación de los resultados. Independientemente de lo potentes que sean las pruebas, el análisis debe responder a la pregunta del estudio.
ESTIMACIÓN DE LA PROBABILIDAD DE EVENTO
Es una práctica común aplicar el método KM para estimar la probabilidad de un evento. La fórmula típica para la estimación de KM es
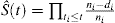
, donde t1t2t3ni representa el número de pacientes en riesgo en el tiempo ti y di es el número de eventos en el tiempo ti.
Esta fórmula se puede transformar mediante manipulación algebraica para expresar la probabilidad de evento como:
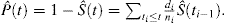
En presencia de RC hay al menos 2 tipos de eventos: evento de interés, identificado con el subíndice e, y evento de riesgo competidor, identificado con el subíndice c. Kalbfleisch y Prentice introdujo la fórmula para la probabilidad de un evento de interés en la presencia de CR:
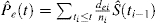
es interesante notar la relación entre (1) y (2). Dado que di es el número de todos los eventos en ti, puede concebirse como la suma del número de eventos de interés dei y el número de eventos de RC dci en el tiempo ti. Como tal, la probabilidad de cualquier tipo de evento se puede descomponer como:
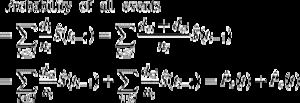
por Lo tanto la probabilidad de todos los eventos puede ser descompuesto en las probabilidades para cada tipo de evento.
Si se utiliza 1 KM para calcular la probabilidad de un evento de interés en presencia de RC, la supervivencia de todos los eventos de la fórmula (2) se sustituye por la estimación de KM basada únicamente en los eventos de interés. Esto sesgará los resultados, como se mostrará más adelante. El principal supuesto para el uso del método de KM es que los pacientes censurados, si se les sigue el tiempo suficiente, eventualmente experimentarán el evento. Sin embargo, cuando se utiliza el método de KM en presencia de RC, los pacientes que experimentan tipos de eventos distintos del evento de interés suelen ser censurados, a pesar de que ya no están en riesgo para el evento de interés. Además, la descomposición agradable vista en (3) no se puede realizar para la fórmula de 1 km.
En situaciones aplicadas es posible que haya varios otros tipos de eventos que no son de interés. En este caso, todos se pueden agrupar bajo el paraguas de eventos CR.
Se mostrará a través de un ejemplo que el uso del método KM no es apropiado en presencia de RC.
Descripción del ejemplo
Se utilizará para ilustrar un conjunto de datos reunido para estudiar los efectos tardíos del tratamiento del linfoma de Hodgkin. El principal resultado es la hospitalización por enfermedad cardíaca. El linfoma de Hodgkin es un tipo de cáncer que aparece principalmente en adultos jóvenes. En sus primeras etapas es casi curable, con una supervivencia general a 10 años del 70%. Por lo tanto, una cohorte de estos pacientes es ideal para estudiar los efectos secundarios a largo plazo del tratamiento. El conjunto de datos utilizado aquí es un subconjunto de una cohorte más grande que se informará en otro lugar. Los datos también se modifican para servir a nuestros fines. Por ejemplo, para simplificar, mantuvimos en los datos solo a los pacientes que recibieron quimioterapia o radiación, excluyendo a los que recibieron tratamiento combinado. Para aumentar la tasa de RC (muerte sin hospitalización cardíaca), se incluyeron pacientes de todas las etapas. Se imputaron algunas fechas de seguimiento y muerte. Debido a las modificaciones que se hicieron a los datos, no se pueden extraer conclusiones clínicas de este análisis. Los datos aquí presentados hacen referencia a 689 registros con 93 hospitalizaciones cardíacas y 467 muertes.
Las tasas de hospitalización cardíaca y de muerte sin evento cardíaco se calcularán utilizando tanto el método KM (1) como la función de incidencia acumulada (CIF) introducida por Kalbfleisch y Prentice21 para este fin (2).
El Método de Kaplan-Meier Aplicado a una Situación de Riesgo en Competencia Sobrestima la Tasa Real del Evento
La Figura 1 presenta las estimaciones CIF y 1 KM para hospitalización cardíaca del grupo tratado con quimioterapia solamente. La línea discontinua correspondiente a las estimaciones de 1 KM está por encima de la línea continua que representa las estimaciones CIF. Se puede demostrar matemáticamente que 1 KM siempre sobrestima la probabilidad de evento. Un error común es que las estimaciones de 1 KM son correctas si los dos eventos son independientes. La independencia entre eventos siempre es cuestionable, en el mejor de los casos, pero incluso cuando los datos se simulan como eventos independientes, existe la diferencia entre las estimaciones CIF y el KM 1. El tamaño de la diferencia depende del número de eventos, tanto para los eventos de interés como para los eventos de RC. En Miyasaka et al., 8 la incidencia de demencia a los 5 años utilizando el método KM fue del 10,5%. El número de RC (muertes) fue de aproximadamente tres cuartas partes del número total de eventos, lo que sugiere que su estimación puede ser mucho mayor de lo observado.
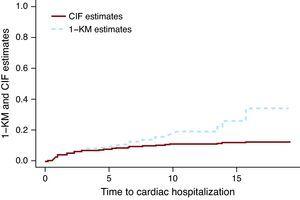
Figura 1. Función de incidencia acumulada frente a estimaciones de 1-Kaplan-Meier.. CIF: función de incidencia acumulada; KM: Kaplan-Meier.
La Función de Incidencia Acumulada Divide la Probabilidad de Cualquier Evento (Hospitalización Cardíaca o Muerte) En las Probabilidades Constituyentes
Algebraicamente esto se demuestra en (3). Sin embargo, para una comprensión más profunda de cómo funciona, se mostrará gráficamente que desde la probabilidad de todos los eventos una parte participa al CIF para un evento y el otro al CIF para el otro evento. La Figura 2A muestra la probabilidad de cualquier evento: hospitalización cardíaca o muerte sin hospitalización cardíaca. La Figura 2B contiene solo la curva entre 10,7 y 10.85 años, de modo que los escalones sean visibles. En cada escalón hay un círculo. Los círculos abiertos aparecen en los escalones en los que se observó una muerte, mientras que los círculos sólidos están en los escalones en los que se produjo una hospitalización cardíaca. Los pasos con círculos sólidos participan en el CIF para la hospitalización cardíaca en el panel C y los con círculos abiertos participan en la curva para la muerte en la Figura 2D, por lo que cada paso contribuirá para la probabilidad del evento que lo causa. De esta manera, en cualquier momento la probabilidad de todos los eventos es la suma de la probabilidad del evento de interés y la probabilidad de CR. Tenga en cuenta que los últimos 3 paneles (Figura 2B-D) muestran la misma ventana de tiempo y tienen la misma longitud para el eje y, de modo que el tamaño de los pasos se puede comparar entre ellos. La Tabla 1 muestra estas probabilidades a 1, 2, 3, 4 y 5 años.
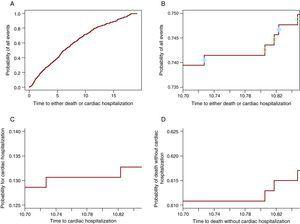
Figura 2. La partición de la probabilidad de todos los eventos en las probabilidades constituyentes. A. La probabilidad de hospitalización cardíaca o muerte. B. La probabilidad de hospitalización cardíaca o muerte solo para la ventana de tiempo 10,70-10,85 años. Los círculos sólidos indican la hospitalización cardíaca y los círculos abiertos representan muertes sin hospitalización cardíaca. C. La probabilidad de hospitalización cardiaca en la ventana de tiempo 10.70 -10.85 años. D. La probabilidad de muerte sin hospitalización cardíaca en la ventana de tiempo 10.70-10.85.
Cuadro 1. La Probabilidad de Cualquier Evento Es la Suma de las Probabilidades Constituyentes.
| Año de presentación de informes | Probabilidad de hospitalización cardiaca | Probabilidad de muerte | Probabilidad de hospitalización cardiaca o muerte |
| 1 | 0.038 | 0.054 | 0.092 |
| 2 | 0.054 | 0.139 | 0.193 |
| 3 | 0.072 | 0.193 | 0.265 |
| 4 | 0.076 | 0.25 | 0.327 |
| 5 | 0.087 | 0.305 | 0.392 |
Debido a que el 1 KM sobrestima la probabilidad de un evento, si tratáramos de agregar las estimaciones de 1 KM para hospitalización cardíaca al 1 KM para muerte, obtendríamos una tasa mucho más alta que la probabilidad de cualquier evento. En algunos casos, el número obtenido es incluso mayor que 1, lo que demuestra que en presencia de RC, las estimaciones de 1 KM ni siquiera son probabilidades.
¿El Método de la Función de Incidencia Acumulada de Hecho Estima la Probabilidad Correcta de Evento?
Para este propósito, se simuló un conjunto de datos de 500 registros de tal manera que no hay censura antes de 5 años y hay 2 tipos de eventos: tipo 1 y 2. La Tabla 2 muestra para cada tipo de evento el número observado hasta ese momento, la tasa bruta y la estimación CIF, que son exactamente iguales. La igualdad ocurre solo cuando no hay observaciones censuradas hasta ese momento. En presencia de observaciones censuradas dentro de los años reportados, la igualdad no se mantiene y la forma correcta de estimar la probabilidad es el CIF y no la tasa bruta.
Cuadro 2. La Probabilidad de los Dos Tipos de Eventos Cuando No Hay Observaciones Censuradas Hasta 5 Años.
CIF, función de incidencia acumulada.
En conclusión, para calcular la probabilidad de evento en presencia de RC se tiene que utilizar el método introducido por Kalbfleisch y Prentice, habitualmente llamado curva de incidencia acumulada.
MODELADO
Un aspecto importante en un análisis es probar la asociación entre una covariable y el evento de interés, ya sea solo o ajustando por otros factores. En ausencia de RC, esto se logra rutinariamente utilizando el modelo de riesgos proporcionales de Cox (PH de Cox).22
En presencia de RC, el modelo de PH de Cox no tiene una interpretación simple. Si el tiempo hasta los 2 tipos de eventos se puede considerar independiente, entonces los resultados se pueden interpretar como que muestran el efecto en la situación en la que no existe RC. Sin embargo, la suposición de independencia rara vez se puede hacer o probar y, por lo tanto, los resultados del modelo de PH de Cox generalmente no son interpretables.
Modelo Fino y Gris
Fino y Gray6 (F&G) modificaron el modelo de PH de Cox para permitir la presencia de RC. La modificación técnica consiste en mantener las observaciones de RC en el conjunto de riesgos con un peso decreciente. De esta manera, el método F&G modela los peligros de subdistribución. El efecto estimado utilizando el modelo F& G muestra las diferencias actuales y reales entre los grupos de tratamiento en términos de ratios de riesgos de subdistribución. El supuesto de la proporcionalidad de los riesgos sigue siendo un requisito, pero, por supuesto, se refiere a los riesgos de subdistribución. El modelo F& G puede acomodar coeficientes dependientes del tiempo para modelar la no proporcionalidad de los peligros. Este modelo se puede aplicar tanto al evento de interés (hospitalización cardíaca) como a la RC (muerte).
Los modelos Cox PH y F& G se aplicaron al conjunto de datos de linfoma de Hodgkin para probar la opción de tratamiento de quimioterapia frente a radiación. Para este ejemplo (Tabla 3), los resultados de los modelos Cox PH y F&G difieren sustancialmente (primeras 2 filas). Como se mencionó anteriormente, los resultados de PH de Cox no son interpretables y no se pueden usar. La segunda fila muestra que hay más hospitalizaciones cardíacas en el grupo de radiación y la tercera fila muestra más muertes en el grupo de quimioterapia. La Figura 3 muestra gráficamente estos resultados. Es posible que se administrara quimioterapia sola a pacientes con enfermedad más avanzada, y que estos pacientes también tuvieran más probabilidades de morir de cáncer. Por otro lado, la radiación sola probablemente se administró a pacientes en un estadio temprano que vivieron más tiempo después del diagnóstico de linfoma de Hodgkin. Estos pacientes tenían más posibilidades de desarrollar efectos secundarios tardíos, como enfermedades cardíacas.
Cuadro 3. El Efecto del Tratamiento Cuando Se Emplean Riesgos Proporcionales de Cox y Modelos Finos y Grises.
IC: intervalo de confianza; PH de Cox: modelo de riesgos proporcionales de Cox; F& G: Modelo fino y gris; HR: razón de riesgos.
Las razones de riesgo muestran el aumento de los riesgos para el grupo de radiación en comparación con el grupo de quimioterapia.
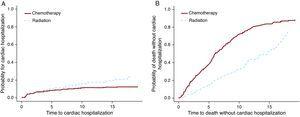
Figura 3. El efecto del tratamiento para la hospitalización cardíaca y la muerte.
Como se puede ver en este ejemplo, la interpretación de los resultados es un trabajo de colaboración entre el estadístico y el clínico que tiene un conocimiento profundo de la enfermedad.
La presencia de RC complica tanto el análisis como la interpretación de los datos. Para que el lector pueda interpretar correctamente los resultados, los autores necesitan incluir detalles sobre los eventos observados, aunque no parezcan importantes a primera vista. Por lo tanto, cuando el criterio de valoración se observa a lo largo del tiempo, los autores necesitan incluir el evento de interés, si existe la posibilidad de RC, cuántos pacientes experimentan cualquiera de estos tipos de eventos y la duración del seguimiento. En presencia de RC es informativo incluir el análisis para el evento de interés, así como el análisis para RC, ya que se complementan entre sí y podrían ayudar a interpretar los resultados.
El Enfoque Logístico
Supongamos primero que estamos en el marco de no CR. Cuando se espera que el resultado ocurra en un intervalo corto (por ejemplo, 1 año), la herramienta de elección para muchos investigadores es la regresión logística. Esto es apropiado si cada individuo de la cohorte tiene el seguimiento mínimo, en este caso 1 año. De hecho, la estimación de la mortalidad a 1 año coincidirá con la estimación de 1 Km. El punto de corte temporal debe ser el mismo para cada individuo de la cohorte. Por lo tanto, si el resultado de interés es la mortalidad a 1 año y 1 individuo de la cohorte muere a 1 año y 2 días, esa persona debe considerarse como «ningún evento a 1 año.»Esto puede reducir el número de eventos, lo que se traduce en un análisis menos que ideal cuando muchos eventos observados ocurren después del punto de corte.
Las mismas reglas básicas se aplican cuando hay presencia de RC. Todas las personas de la cohorte deben tener el seguimiento mínimo elegido como punto de corte de tiempo, y ese punto de corte debe aplicarse a todas las personas de la cohorte. Los coeficientes y los valores de p en general darán el mismo mensaje,pero no serán exactamente los mismos para la regresión logística en comparación con el modelo F&G. En primer lugar, en la regresión logística el coeficiente representa el log de la odds ratio, mientras que en el modelo F&G es el log de la razón de las subdistribuciones de peligros. Además, en el análisis logístico no se utilizan todos los eventos y, por supuesto, se utiliza un modelo diferente.
CÁLCULO DE POTENCIA
Cuando la medida es time-to-event, el cálculo de potencia tiene dos etapas. El primer paso es calcular el número de eventos necesarios para detectar un tamaño del efecto. A continuación, se calcula el número de pacientes necesarios para observar ese número de eventos. Se enfatizó en las secciones anteriores que cuando la RC está presente no es posible observar todos los eventos de interés debido a la ocurrencia de la RC. Dado que el número de eventos es central en el cálculo de la potencia, se debe tener especial cuidado para garantizar que se tengan en cuenta los RC. Si no se considera la RC, el estudio tendrá poca potencia y, por lo tanto, probablemente no tenga éxito (y posiblemente no sea ético).
SOFTWARE
El software R de código abierto en el sitio CRAN (the Comprehensive R Archive Network) (http://cran.r-project.org/) ofrece un paquete (cmprsk) implementado por Dr. Robert Gray contiene las herramientas necesarias para un análisis completo de la contabilidad de CR. Así, se podrían obtener gráficas de probabilidad observadas para el evento de interés y un valor de p basado en la prueba de Gray, que es una prueba de progreso modificada para la situación de RC. Dentro del paquete también hay una función para modelar usando el enfoque F&G. Luca Scruca mejoró la entrega de salida de la función de modelado para una lectura más fácil al incorporar en el paquete una función de tipo resumen. El modelo tiene la posibilidad de verificar la proporcionalidad de los peligros, y se pueden incluir términos para coeficientes dependientes del tiempo. El código no puede acomodar datos de truncamiento izquierdo o de clúster. El truncamiento izquierdo sería útil para el análisis de eventos múltiples/recurrentes por paciente o para el análisis de cohortes de casos. Se elaboró un código para estudios de casos y cohortes (Pintilie et al.23) y se puede obtener de los autores. Zhou et al.24 se amplió el modelo F& G para acomodar datos estratificados y también tendrá una versión para datos de clúster. En este punto, el código se puede obtener de los autores para ambos casos, pero es probable que se envíe al CRAN.
STATA 11 ha implementado recientemente el modelo F& G. Es necesario tener en cuenta que los gráficos obtenidos utilizando STATA son gráficos predictivos en lugar de gráficos de probabilidad observados. Hay dos advertencias cuando se utilizan curvas predichas: a) las líneas siempre aparecerán como si se cumpliera la proporcionalidad de los peligros, y b) el número de pasos en cada curva será mayor que el número de eventos en cada subgrupo, dando la impresión de que hay más eventos de los que realmente hay.
CONCLUSIONES
La disponibilidad de grandes conjuntos de datos con seguimiento completo para varios criterios de valoración aumenta continuamente. También hay una creciente necesidad de análisis que se ocupen de un punto final preciso como la muerte por insuficiencia cardíaca o el control de la enfermedad o el control de la enfermedad local. Todos estos criterios de valoración podrían tener RC. Por lo tanto, es esencial que el RC se considere desde la etapa de diseño hasta la interpretación de los resultados. Si bien el modelo de PH de Cox puede tener un valor limitado cuando se considera la independencia, las estimaciones de KM no son correctas y no pueden interpretarse. Por lo tanto, es necesario aplicar técnicas específicas como los modelos CIF y F&G disponibles en R y parcialmente en STATA.
CONFLICTOS DE INTERESES
Ninguno declarado.