Capofamiglia Trasformazione
Capofamiglia Trasformazione (anche il “Padrone di casa di Riflessione”) è ortogonale a riflessione trasformazione:
- è la reflex vettori nelle colonne della matrice tale che
- il primo vettore ha tutti zeri tranne il primo elemento
La Matrice di Trasformazione
Riflessione trasformazione:
Proprietà
matrici di Householder sono simmetriche e ortogonale: sono matrici di riflessione
Derivazione
Quindi abbiamo P P = I-2vv^T$:
usiamo tali trasformazioni per l’azzeramento elementi
la Decomposizione QR
Come nel caso di Decomposizione LU, dove abbiamo applicato una serie di Gauss modifiche di Trasformazione, siamo in grado di fare lo stesso e di eseguire una serie di Trasformazioni di Householder
- quindi, se si seleziona $y = \pm e_1$ (dove $e_1$ è la matrice con 1 in posizione 1 e il resto sono zeri)
- quindi non sarà a zero tutti gli elementi di $x$, tranne il primo
- così, la scelta appropriata di $H$, possiamo prendere $A$ e zero tutti i sub-diagonale elementi
- può farlo più volte per ogni colonna di $A$
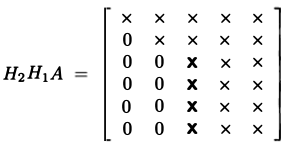
in Questo modo siamo in grado di eseguire la Decomposizione QR:
Hessenberg Decomposizione
Invece di utilizzare per l’abbassamento della matrice Triangolare, siamo in grado di utilizzare al Padrone di casa, di Trasformazione, di ridurre una matrice di Hessenberg Matrice